反比例はどんな問題で使えるの？ 算数でも理科でも役立つ考え方を理解しよう

「xの値が2倍、3倍、…になると、yの値が\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、…になる」という関係が成り立つとき、「yはxに反比例する」といいます。算数の授業でサラッと流されがちな反比例ですが、実は算数だけでなく理科でもとても大切な考え方です。反比例がどのような場合に成り立つのかを理解しましょう。

反比例を算数で使ってみよう

「yはxに反比例する」を式で表すとどうなるのでしょうか。表に整理しながら考えてみましょう。

反比例は「x×y＝決まった数」で表せる

反比例のわかりやすい例として、縦がxcm、横がycmで、面積が12cm\(^2\)の長方形を考えてみます。

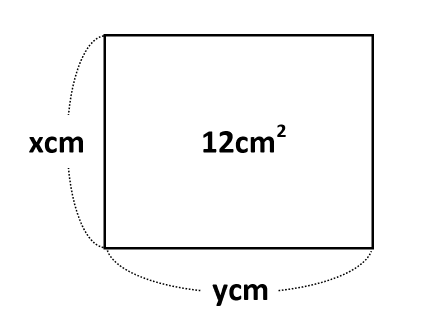
面積が12cm\(^2\)と決まっているので、x＝1ならy＝12、x＝2ならy＝6、……です。これをまとめたのが下の表です。

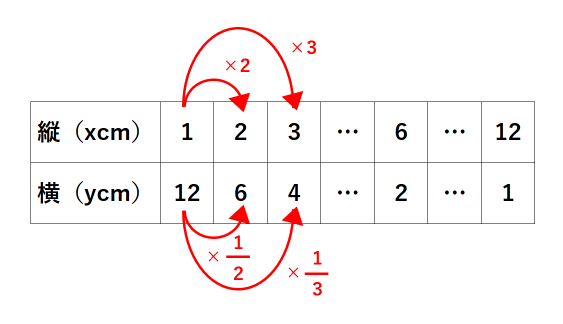
xの値が2倍、3倍、…になると、yの値が\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍、…になっているのがわかります。さらに、x×yはいつでも12です。このことから、反比例の式は「x×y＝決まった数」も表せることがわかります。（算数では「y＝きまった数÷x」で表すことが多いです）

また、xとyが反比例するとき、xの比が2：3ならば、yの比は\(\frac{1}{2}\)：\(\frac{1}{3}\)＝3：2です。つまり、xとyの比は逆比（逆数の比）になります。

反比例を利用して歯車の問題を解く

「x×y＝決まった数」と表せるなら、xとyは反比例の関係にあります。これは長方形の面積以外でも成り立ちます。

反比例では歯車がよく登場します。歯車Aと歯車Bがかみ合っているなら、歯車Aと歯車Bで「歯数×回転数＝一定」です。そのため、歯数と回転数は反比例の関係で、歯数と回転数の比は逆比で表せます。

歯車Aと歯車Bの歯数の比は50：40＝5：4なので、回転数の比はその逆比で4：5です。求める回転数をxとすると、8：x＝4：5よりx＝10回転が答です。

反比例を利用して速さの問題を解く

「速さ×時間＝道のり」なので、道のりが一定ならば、速さの比と時間の比は逆比です。これも反比例の一種です。