算数では暗記よりも思考力が大切？ 計算や数字を覚えることのメリットとデメリット

算数を教える塾講師や家庭教師の間では、「算数でも暗記が必要だ」という意見と「算数では暗記せずに思考力を鍛えるべきだ」という意見がしばしば対立します。実はどちらの意見も間違いではありません。算数にも覚えるべき知識はありますが、何でもかんでも丸暗記していると大抵は行き詰まります。今回は、計算や解法などを覚えることのメリットとデメリットについて紹介します。

算数では何を暗記するかが大切

算数でも暗記すべき知識はありますし、暗記すると便利な計算や解法もあります。それぞれを整理しましょう。

［1］定義は絶対に暗記しなければならない

「素数」とは「1とその数自身以外に約数の無い整数」です。このような定義（言葉の意味）は暗記が必要です。定義は考えてわかるものではありませんし、「18と24の公約数を求めなさい」のような問題は公約数の定義を知らなければ絶対に解けません。覚えておくべきは、「偶数」「奇数」「倍数」「約数」などの数の定義と、「平行四辺形」「台形」「柱体」「錐体」などの図形の定義です。

［2］公式の多くは暗記しなくてもよい

和差算では「（和＋差）÷2＝大きい数」「（和－差）÷2＝小さい数」という公式を覚えなくても、線分図を描けば問題を解けます。しかも、公式は和差算でしか使えませんが、線分図は損益算や倍数算などにも応用できるので便利です。特殊算の公式の多くは暗記不要です。一方、錐体の体積公式や4の倍数の見分け方などは小学生には証明不可能なので暗記するしかありません。

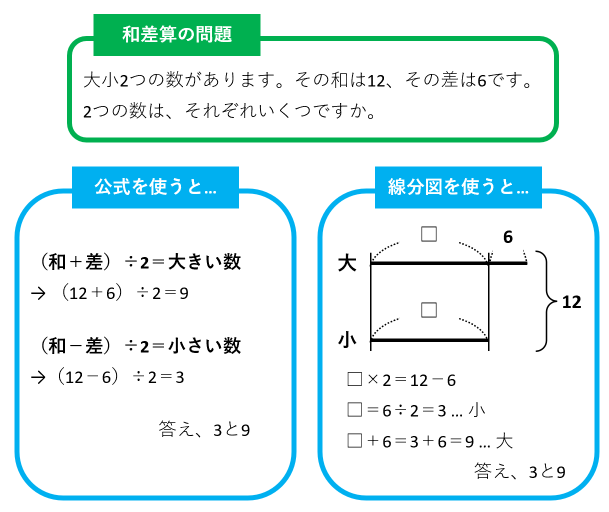
［3］理解しているならパターン暗記してもよい

旅人算で「出会いは速さの和、追い越しは速さの差」と覚えてしまうと、出会いなのに速さの差を使う問題を解けません。一方で、このような罠にひっかからないくらいに理解しているなら、パターン暗記で解法を整理するのもよいでしょう。特に図形問題は、等積変形や連比の利用などのパターンを覚えていないと厳しい場合が多いです。