数学の証明は中学受験生でもできる？ 算数でも論理的に説明する力が役に立つ

小学算数と中学数学の大きな違いに証明の有無があります。算数では、中学入試の問題も含めて、計算して答えを出すことが中心です。一方、数学では、既に与えられた答えが正しいことを文章で説明していく証明が登場します。多くの中学受験生は「算数の勉強に証明は関係ない」と思うでしょう。しかし、実は証明の考え方に慣れていると、算数でも有利になります。今回は、数学の証明を算数の勉強に役立てるコツをお伝えします。

図形問題を論理的に解ける

中学受験算数では、三角形の合同や相似を利用した図形問題が定番です。一方、中学数学では、合同や相似に証明問題が加わります。

証明の代表は三角形の合同と相似

2つの図形が合同であるとき、これらの図形は形も大きさも同じです。一方、2つの図形が相似であるとき、これらの図形は形が同じで大きさが異なります。

数学では、合同条件と相似条件を利用して、2つの三角形の合同や相似を証明していきます。中学受験算数では相似がよく出ますが、特に「2組の角がそれぞれ等しい」という相似条件をヒントにすれば相似な三角形を簡単に見つけられる問題がほとんどです。

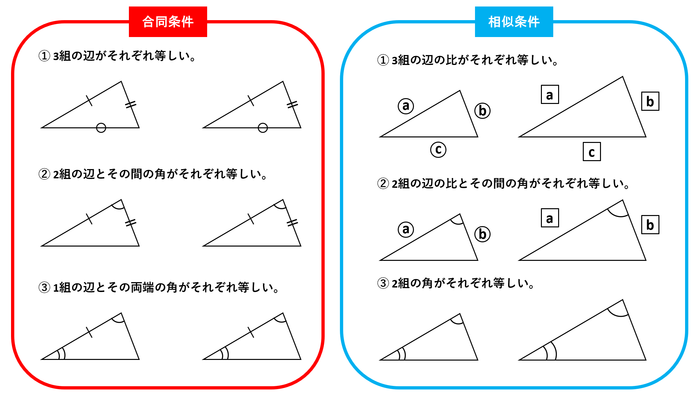
証明できれば図形問題が得意になる

中学受験算数の図形問題では、辺の長さや面積を求める計算問題しか出ません。しかし、合同な三角形や相似な三角形を正しく見つけられないと、決して正解にはたどり着けません。それにもかかわらず、中学受験生の多くは、合同な三角形や相似な三角形を見た目で見つけようとして、見つけるまでに時間がかかったり、誤った三角形を合同や相似だと思い込んだりします。図形問題が苦手になる原因です。

見た目で合同や相似を判断するクセを克服するには、きちんと証明することが大切です。中学数学のように厳密な記述は必要ありませんが、「三角形ABCと三角形EDCは、角ACB＝角ECD、角ABC＝角EDCが等しくて、2組の角がそれぞれ等しいから相似だ」のように常に言葉で確認するようにするとよいでしょう。証明を意識して考えられれば、合同な三角形や相似な三角形を見つけやすくなって、図形問題が得意になります。