階差数列をわかりやすく解説！ 規則性に着目すれば三角数も簡単に解ける

中学受験算数の数列で、多くの受験生が階差数列を苦手とします。

階差数列とは、ある数列の隣り合う数同士の差からできる別の数列のこと。今回は、この階差数列について基本から解説し、実際に問題を解いていきます。

階差数列の基本

階差数列は基本を理解していれば決して難しくありません。

階差数列とはどのような数列か？

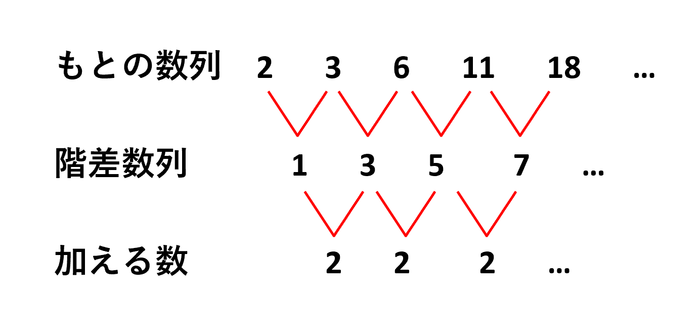
2、3、6、11、18、…

この数列で、隣り合う数同士の差を取ってみましょう。そうすると、3－2＝1、6－3＝3、11－6＝5、18－11＝7、…という数を得られます。これらの数を並べると次の通りです。

1、3、5、7、…

これらの数は、初めの数（初項）が1、加える数（公差）が2の等差数列になっています。このように、ある数列の隣り合う数同士の差からできる数列は「階差数列」と呼ばれます。

上の例のように、中学受験では多くの場合、階差数列は等差数列になります。等差数列とは、隣り合う数同士の差が同じ数になる数列です。

階差数列ともとの数列の関係は？

上の例を使って、階差数列ともとの数列の関係を考えてみましょう。

まず、もとの数列の2番目の数は2＋1＝3です。もとの数列の1番目の数2に、階差数列の1番目の数1を足しています。次に、もとの数列の3番目の数は2＋1＋3＝6です。もとの数列の1番目の数2に、階差数列の1～2番目の数の和1＋3を足しています。

同様に考えると、階差数列ともとの数列の間には、

「もとの数列の初めの数＋階差数列の1～（N－1）番目までの数の和＝もとの数列のN番目の数」

という関係があることがわかります。これを公式として覚えるよりも、具体的に数字を書き出して、その場でもとの数列のN番目の数を求められるようにするとよいでしょう。

階差数列の問題の解法

階差数列の問題を実際に解いてみましょう。規則性がすぐにわからない数列は、隣り合う数同士の差を取ってみるのがコツです。

階差数列の基本問題

まず、隣り合う数同士の差を取って階差数列を求めます。10－2＝8、24－10＝14、44－24＝20、70－44=26、102－70＝32、…なので、階差数列は次の通りです。

8、14、20、26、32、…

この数列は、初めの数が8、加える数が6の等差数列です。

次に、もとの数列の30番目の数を求めるので、階差数列の29番目の数を求めます。