
平方数と立方数とは? 相似や数列の問題を解くときに役立つ「特別な整数」を解説
中学受験算数でよく出てくる数に平方数と立方数があります。これらの特別な数字を見分けられるようにして、どこで使えるのかを理解することが大切です。
平方数と立方数とは何か?
塾の算数の授業では「平方数」「立方数」という言葉を聞くこともあるでしょう。それぞれの意味を理解して、しっかり見分けることが大切です。
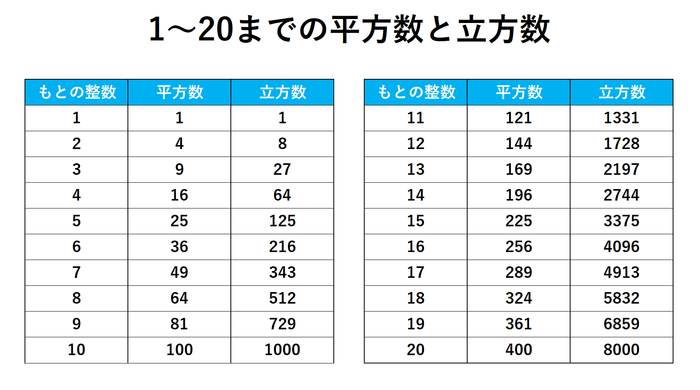
平方数と立方数
平方数は同じ数を2回かけた(2乗した)数で、立方数は3回かけた(3乗した)数です。たとえば、3の平方数は3×3=9で、立方数は3×3×3=27です。また、11の平方数は11×11=121で、立方数は11×11×11=1331です。
面積の単位には「平方メートル」があります。この「平方」は「メートルを2回かける」という意味です。そもそも「平方する」が「2回かける」を意味することは覚えておくとよいでしょう。同じように、「立方する」は「3回かける」なので、体積の単位の「立方メートル」は「メートルを3回かける」という意味だとわかります。
平方数と立方数の見分け方
平方数のうち10×10までは九九で見分けられます。一方、九九に含まれない平方数や、九九からは判断しにくい立方数は、素因数分解することで見分けられることがあります。
素因数分解とは、ある整数を素数の積で表すことです。素数は1と自分以外で割り切れない数です。素数には2、3、5、7、11、13、…があります。
216を素因数分解してみましょう。216=2×2×2×3×3×3なので、2と3をそれぞれ3回かけた数だとわかります。つまり、216は2×3=6の立方数です。
九九や素因数分解で見つけにくい平方数・立方数は覚えてしまうとよいでしょう。たとえば、13の平方数は169で、立方数は2197です。語呂合わせを考えながら覚えるのもおもしろいかもしれません。
平方数と立方数はどこで使うのか?
平方数と立方数をどこで使うのかを理解しておくことは大切です。
相似
形は同じで大きさが違う図形同士を「相似な図形」といいます。相似な図形では、一方の図形を拡大・縮小したとき、もう一方の図形と重なり合う辺があります。これらの辺が「対応する辺」で、対応する辺の比が「相似比」です。
相似な図形では、相似比がわかっていると、「相似比×相似比=面積比」「相似比×相似比×相似比=体積比」が成り立ちます。したがって、面積比では平方数が、体積比では立方数がそれぞれ登場します。
【問題1】下の図のように円錐Aと円錐Bがあります。AとBは相似です。このとき、次の問いに答えなさい。
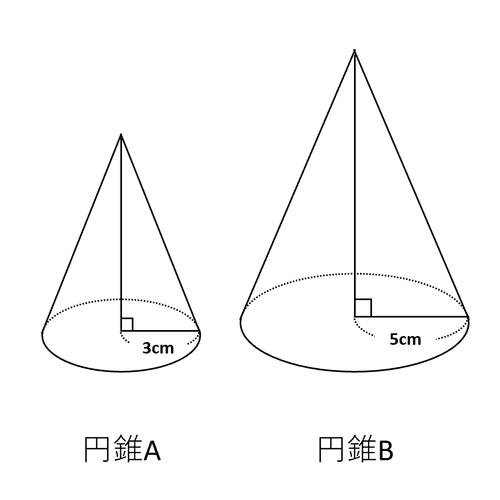
(1) 円錐Aと円錐Bの表面積の比を求めなさい。
(2) 円錐Bの体積が100cm\(^3\)のとき、円錐Aの体積は何cm\(^3\)ですか。
円錐Aと円錐Bの底面の半径はそれぞれ3cmと5cmです。半径の比がそのまま相似比になるので、相似比はA:B=3:5です。
(1) 相似な立体図形の面積比は相似比を平方することで求められます。したがって、表面積の比はA:B=3×3:5×5=9:25です。
(2) 相似な立体図形の体積比は相似比を立方することで求められます。したがって、体積比はA:B=3×3×3:5×5×5=27:125です。Aの体積を□cm\(^3\)とすると、27:125=□:100より□=27×100÷125=\(\frac{108}{5}\)=21\(\frac{3}{5}\)(cm\(^3\))が答えです。
数列
数列の問題では、平方数が規則性のヒントになることがあります。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます


