年齢算は線分図を書けば簡単に解ける！ 比の応用問題も差に注目すれば難しくない

親子や兄弟姉妹などの年齢を題材にした特殊算が「年齢算」です。比が絡むことが多いため、苦手意識のある受験生も少なくありません。今回は、年齢算を解くためのコツをわかりやすく解説します。

年齢算を線分図で解く

年齢算を解くのに便利なのが線分図です。線分図をどのように書いて、どこに注目すればよいのかを紹介します。

何年経っても年齢差は一定

年齢算のポイントは、何年経っても年齢差が一定であることです。たとえば、現在の兄が15歳、弟が13歳ならば、年齢差は2歳です。5年後に兄は20歳、弟18歳になりますが、年齢差はやはり2歳で変わりません。この年齢差に注目することで多くの年齢算を解くことができます。

年齢算で線分図を使うときのコツ

年齢算の基本問題を解きながら、実際に線分図を書いてみましょう。

お父さんの年令が太郎君の年令の5倍になるのは□年後とします。「□年後」「□年前」は、下の線分図のように左側に寄せてしまうと見やすくなります。

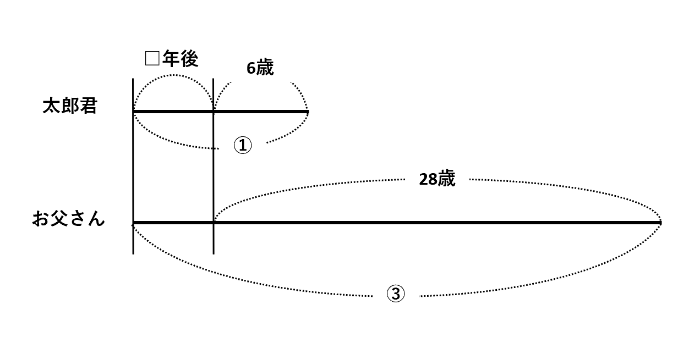
線分図を書いたら、年上と年下の年齢差（下図の赤線部分）に注目しましょう。何年経っても年齢差が一定なので、年齢差22歳＝比の差2がわかります。したがって、比の1＝11歳です。太郎君の線分を見て、□＝（比の1）－6歳＝11－6＝5（年）が答えです。

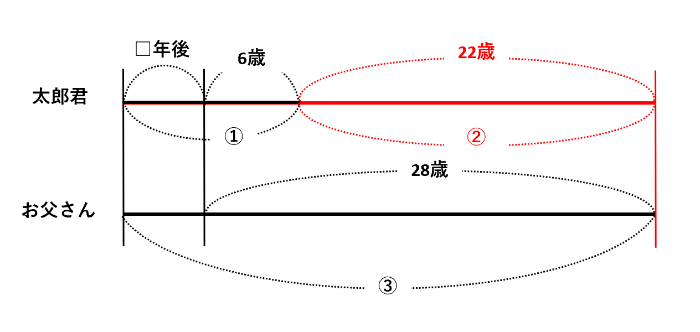
年齢算の応用問題を解く

年齢算では登場人物が2人だけとは限りませんし、具体的な年齢がわかっているとも限りません。苦手な受験生の多い応用問題の解き方を解説します。

弟や妹が生まれる問題

お母さん、太郎君、次郎君の年齢を線分図で表してみましょう。見やすいように、太郎君と次郎君が生まれる前は点線で、生まれた後は実線で書きました。

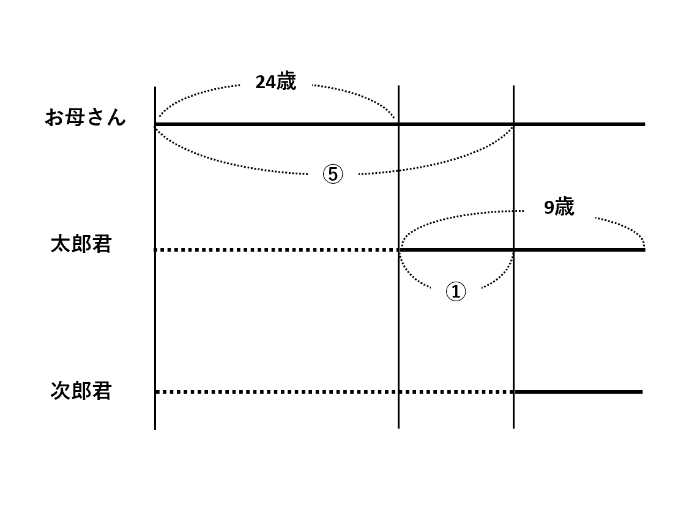
この線分図を眺めながら、年齢差と比の差が等しくなる線分を探します。そうすると、下の図のように、24歳＝比の4であることがわかります。

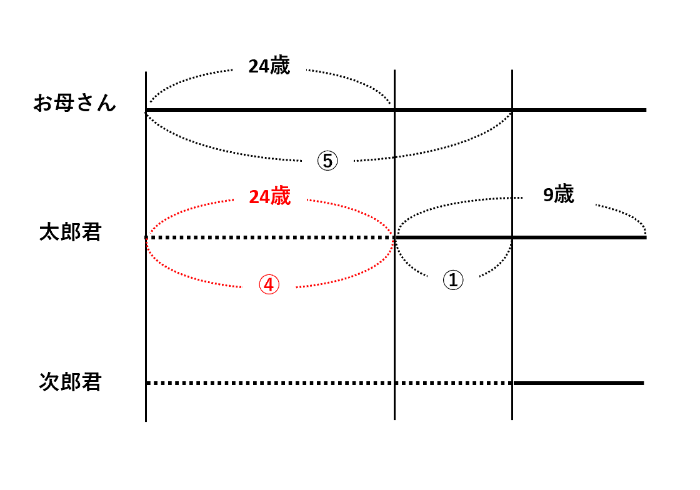
比の4＝24歳なので、比の1＝6歳です。現在の次郎君の年齢＝現在の太郎君の年齢－比の1＝9－6＝3歳です。

登場人物が3人以上の問題

【問題3】のように、登場人物が3人以上で、何人かの年齢の和を考える問題は要注意です。太郎君と次郎君の年齢の和がお父さんの年齢に等しくなるのが□年後だとして、線分図を書いてみました。

ポイントは、太郎君と次郎君を1人と考えることです。そうすると、□年後、お父さんの年齢は（26＋□）歳になるのに対して、太郎君と次郎君の年齢の和は（8＋□×2）歳になります。太郎君と次郎君の年齢の和を（8＋□）歳にしてしまう間違いが多いので要注意です。3人を1人と考えれば□×3、4人を1人と考えれば□×4、……となることを覚えておくとよいでしょう。

ここまで書いたところで、年齢差と□で表した差が等しくなる線分を探します。下の図のように、□＝18を見つけられれば、答えが18年後だとわかります。

年齢が全くわかっていない問題

【問題4】は、太郎君の年齢もお父さんの年齢もわかっていないのが他の問題との違いです。このような問題でもまずは線分図を書いてみましょう。下の線分図では、現在の年齢の比1：4を○で、14年後の年齢の比1：2を□で囲いました。比を区別するために○や□を使い分けましょう。

年上と年下の差に注目するのは他の問題と同じです。下の図の赤線部分から、比の差である○の3＝□の1がわかります。

比を○にそろえると、○の2＝14年なので、現在のお父さんの年齢＝○の4＝28歳とわかりました。【問題4】のように、具体的な年齢が全くわかっていない問題も、線分図を書いて連比を利用すれば解けます。

年齢算は決して難しくない

年齢算は比の単元に含まれていることが多く、「比」という言葉から「難しい」と思い込む受験生も少なくありません。確かに、比の式だけで解こうとすると、イメージがつかみづらくて難易度は高くなります。しかし、実際は、線分図を書ければ簡単に解けてしまう問題がほとんどです。苦手意識のある受験生には、線分図を使って解いてみることをおすすめします。

※記事の内容は執筆時点のものです