やりとり算は割合も出てくるので難しい？ 線分図ややりとり図を描けば簡単に解ける

足し算と引き算の応用問題に「やりとり算」があります。

答えに至る過程が複雑なことに加え、多くの問題では割合と絡むため、苦手とする中学受験生は少なくありません。一方で、図を描きながら丁寧に解いていけば、確実に正解できる問題であるのも確かです。

今回は、やりとり算の解き方を分かりやすく解説します。

やりとり算を線分図で解く

やりとり算とは、お金やものなどを渡したり受け取ったりした後の状態から最初の金額や個数などを求める問題です。金額や個数などが具体的な場合は線分図で解くのが簡単です。実際に【例題1】を考えてみましょう。

やりとり算で線分図を描く場合、まずは最後の状態を線分で表します。【例題1】では、3人の所持金が2000円になった状態を線分図にしました。

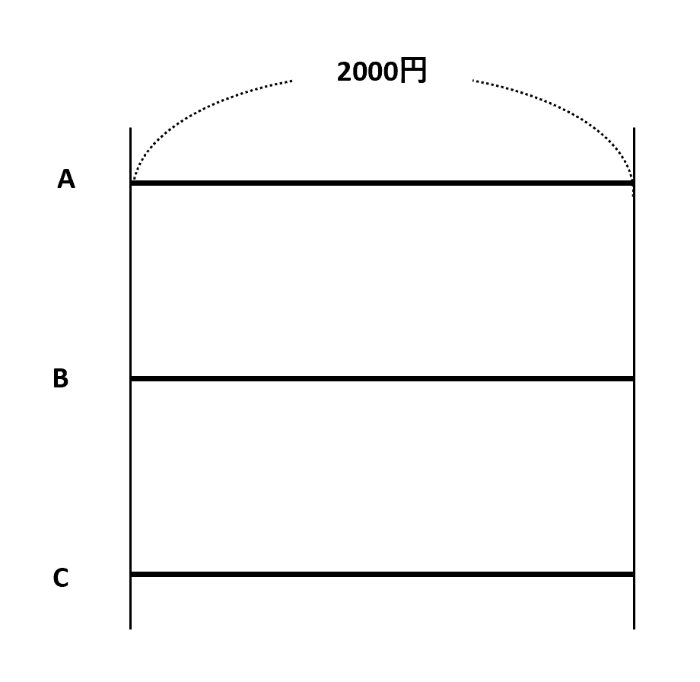
この線分図にお金の流れを書き込んでいきます。ポイントは、後ろの金額から逆の流れを書いていくことです。【例題1】では「最後にCがAに600円をわたしました」とあるので、AからCに600円を戻します。

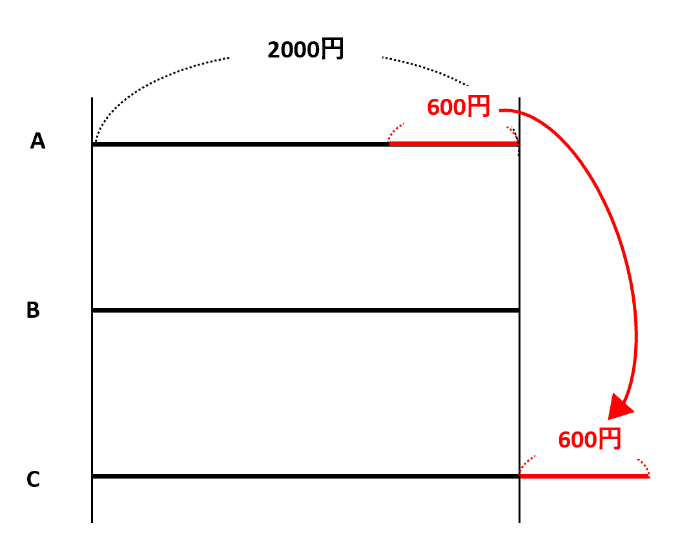
同じように、CからBに300円を戻し、BからAに400円を戻します。その結果、はじめの所持金は、Aが2000－600＋400＝1800（円）、Bが2000＋300－400＝1900（円）、Cが2000＋600－300＝2300（円）とわかりました。

線分図を軽視するのは危険！ 中学受験をするなら低学年から線分図を練習しておきたい理由

「線分図」をご存知でしょうか？ 小学校では2年生で「テープ図」として学習するので、テープ図という名前なら知っているとい...

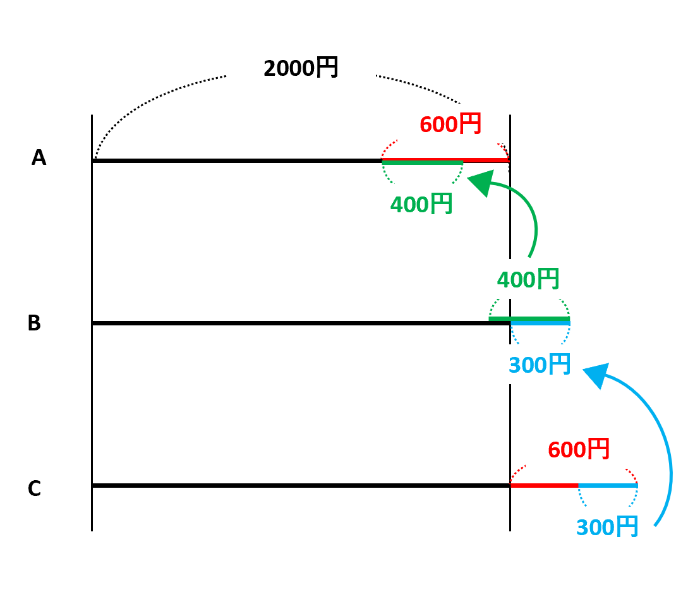
やりとり算をやりとり図で解く

割合や比が出てくる問題は、線分図よりもやりとり図の方が解きやすくなります。