ばねの直列つなぎと並列つなぎの違いは？ 少し複雑な計算問題をわかりやすく解説

複数本のばねをつなぐと、1本のときとは違った伸び方をします。このときのつなぎ方に直列つなぎと並列つなぎがあります。それぞれをしっかり理解して、少し複雑な計算問題も解けるようにしましょう。

ばねの基本を理解する

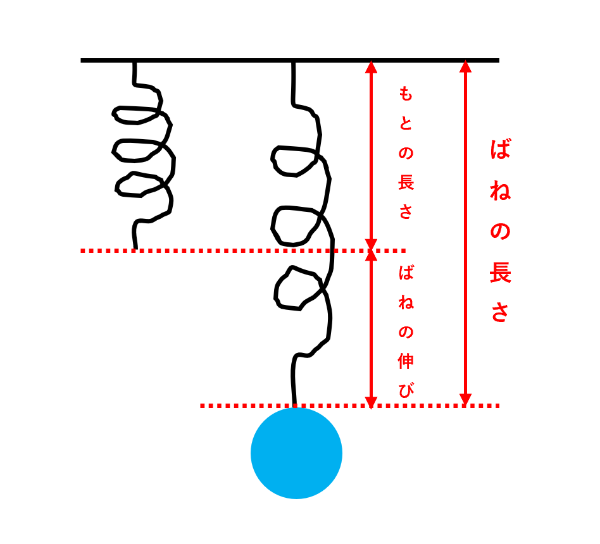
ばねを考えるときに大切なのは言葉の違いです。「ばねの長さ」「ばねの伸び」「もとの長さ」をしっかり区別しましょう。

「ばねの長さ」と「ばねの伸び」

おもりをつるしていない（力を加えていない）ときのばねの長さを「もとの長さ」といいます。「自然長」と呼ばれることもあります。ばねが伸びたり縮んだりしていない状態です。

おもりをつるしたばねは伸びて、もとの長さよりも長くなります。もとの長さよりも伸びた長さが「ばねの伸び」で、ばね全体の長さが「ばねの長さ」です。下の図から、「ばねの長さ＝もとの長さ＋ばねの伸び」という関係もわかるでしょう。

ばねの伸びはおもりの重さに比例する

ばねの伸びはおもりの重さ（加える力の大きさ）に比例します。これを「フックの法則」といいます。たとえば、10gのおもりをつるすと1cm伸びるばねは、20ｇのおもりをつるすと2cm、30gのおもりをつるすと3cm伸びます。

一方、ばねの長さはおもりの重さに比例しません。10gのおもりをつるしてばねの長さが11cmになっても、20ｇのおもりをつるしてばねの長さが22cmになるわけではありません。ばねの長さを求めるときは、フックの法則を利用してばねの伸びを求め、もとの長さに加えます。

ばねの直列つなぎと並列つなぎ

複数本のばねをつなぐ場合、そのつなぎ方には直列つなぎと並列つなぎがあります。

ばねの直列つなぎ

複数本のばねを1本の線になるようにつなぐのが直列つなぎです。直列つなぎしたばねは伸びやすくなります。

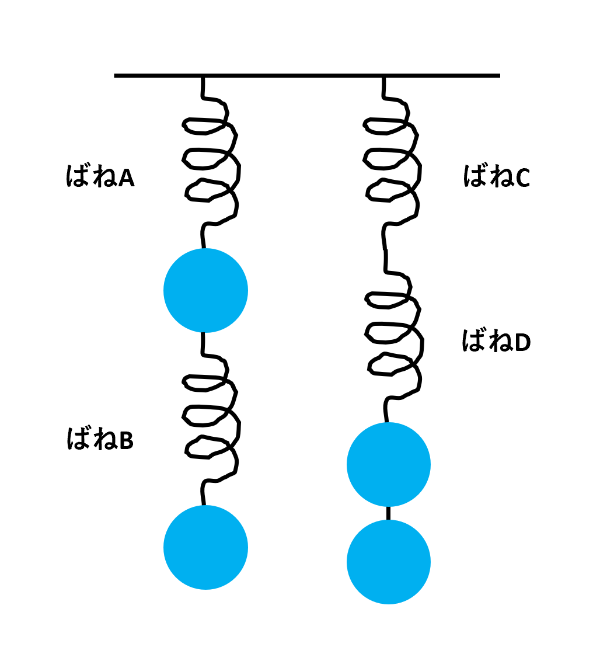
【問題1】はばねの長さを求める問題ですが、まずはばねの伸びを求めましょう。

ばねAとばねB、ばねCとばねDがそれぞれ直列つなぎです。直列つなぎのばねの伸びを求める場合、それぞれのばねの下につるされているものの重さを考えます。

ばねAはその下におもり2つとばねBがつるされています。ばねの重さは考えないので、おもり2つだけの重さを考えると、20×2＝40（g）です。10gのおもりをつるすと1cm伸びるので、40gで4cm伸びます。したがって、もとの長さの10cmに4cmを加えて、ばねAの長さは14cmです。

同様に、ばねBはその下に20gのおもり1つがつるされているので、2cm伸びます。したがって、ばねBの長さは12cmです。

また、ばねCもばねDも、それぞれの下に20gのおもり2つ（40g）がつるされているので、どちらも4cm伸びます。したがって、ばねCの長さもばねDの長さも14cmです。

ばねの並列つなぎ