【理科】生存曲線とは？ 5つのステップをもとにスッキリと理解しよう

中学入試の理科で、ここ最近よく扱われるようになったテーマがあります。

それが、生存曲線です。

私のイメージだと、生存曲線は高校の生物で習う単元なのですが……。たしかに渋谷幕張中や栄東中など、実際の中学入試でもガッツリ出題されています。

しかし、このテーマは注意が必要です。扱うグラフが特殊だったり、生存率を計算させられたりと、小学生にとってはちょっと難しめな内容だからです。

そこで今回は「５つのステップ」をもとに、小学生でも生存曲線をスッキリと理解できるように解説していきます。最後のステップまでしっかりと目を通しつつ、生存曲線の問題を解く力を身につけましょう！

5つのステップ

ではさっそく、5つのステップを見ていきましょう。

STEP1：生存曲線のイメージをつかもう！

はじめに、生存曲線についてのイメージをつかみましょう。「生存曲線」という言葉はちょっと堅苦しくて、わかりづらいので、イメージしやすいようにザックリとした表現を使っていきます。

まずは、生き物が誕生してから寿命にいたるまでの「生き残る様子」をイメージしてみましょう。

下の図を見る限り、生き物の種類によってその様子が違うことがわかりますね。

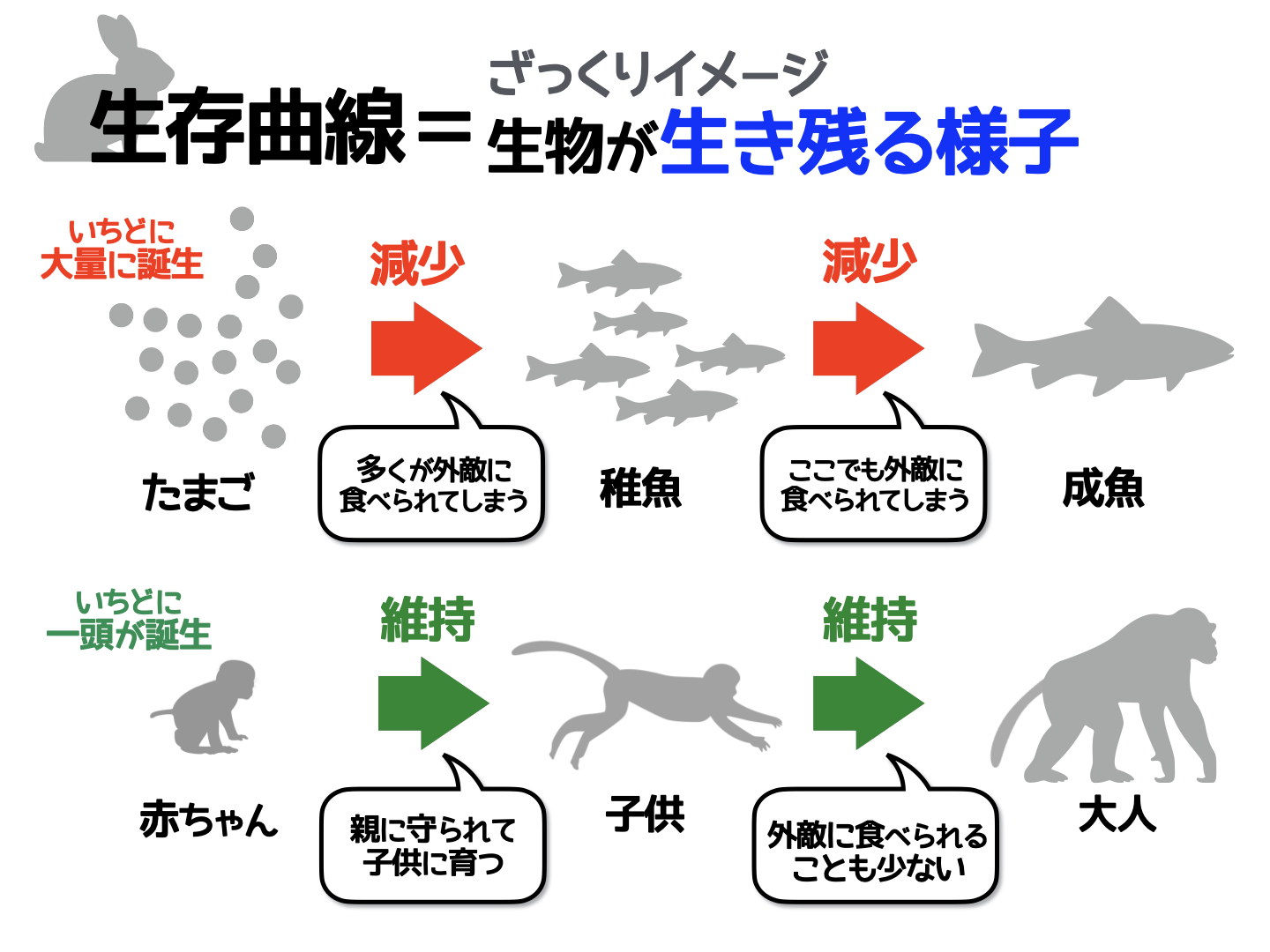
たとえば魚はどうでしょう。魚は大量に卵を産みますが、卵のうちに、その多くがほかの動物によって食べられてしまいます。なんとか孵化できた魚も、稚魚のうちに多くが食べられてしまいます。そして少数だけが成魚になり、寿命を迎えます。

一方で、猿はどうでしょう。猿は一度に多くの子供を産みません。だいたいの猿が一度に１頭の子供を産み、子供は親に大切に守られながら育てられます。そのため病気や事故などがない限り、そのまま大人になり寿命を迎えます。

これが、生き物の「生き残る様子」についてのザックリとしたイメージです。

「生き残る様子」をグラフにしたものが生存曲線

「生き残る様子」をグラフで表したものが、ズバリ生存曲線です。

縦軸に「生きている数」、横軸に「産まれてから寿命までの時間」をとったグラフを書くと、以下のようになります。生存曲線とは、その名のとおり「生き物の生きている数をグラフにした曲線」というわけですね。

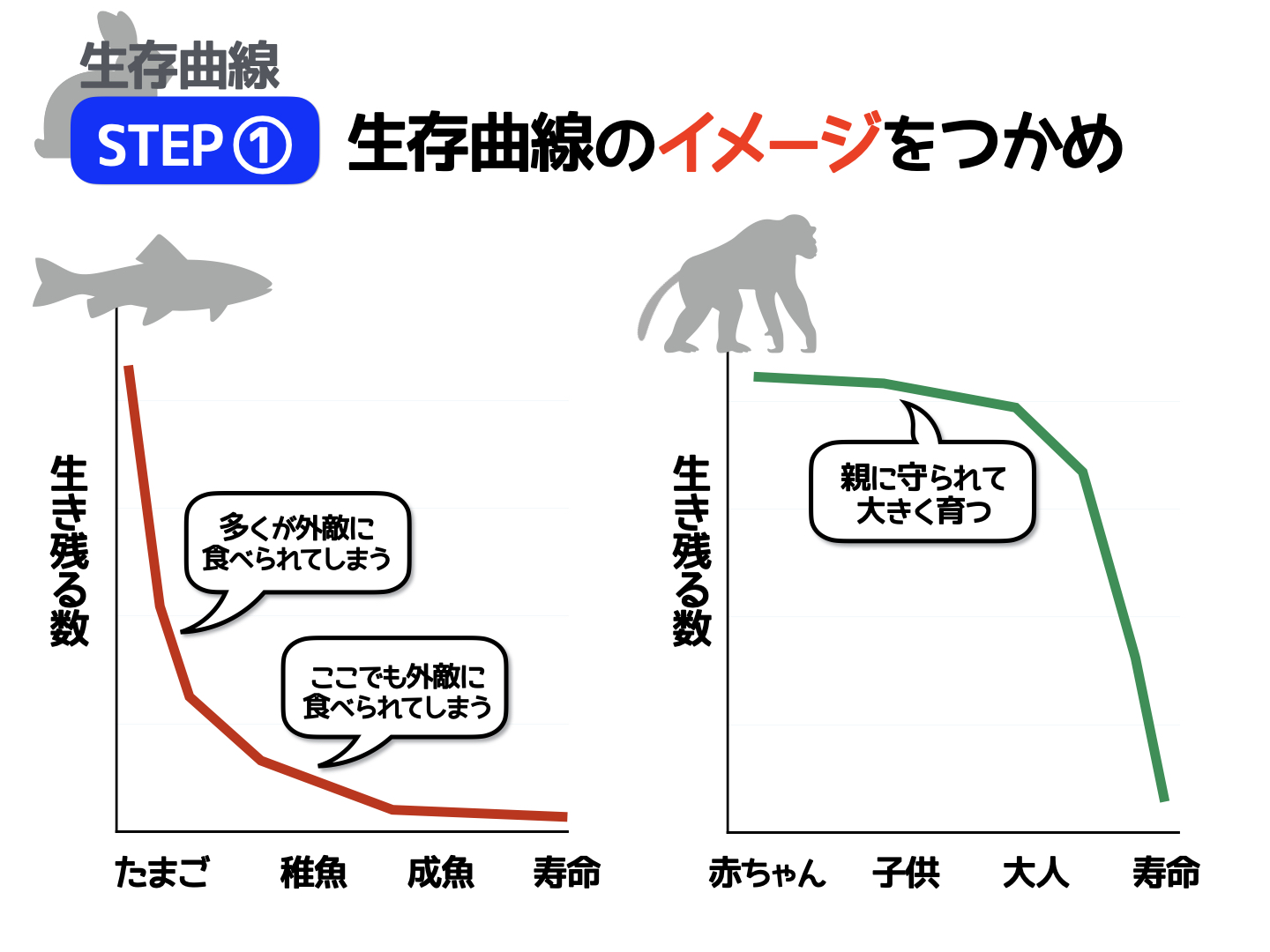
生存曲線のイメージはつかめましたか？

では次に、中学入試を攻略するうえで大切なステップに移りましょう！

STEP2：生存率の表を着実に埋めよう！

生存曲線を正しく理解するうえで、まず押さえておきたいのが「生存率の表」です。実際の入試問題でも、ほとんどの問題が生存率の表をベースに設問が展開されています。

生存率の表を見ることで、それぞれの生物が生き残っていく様子がまったく異なっている、ということを読み取ることができます。

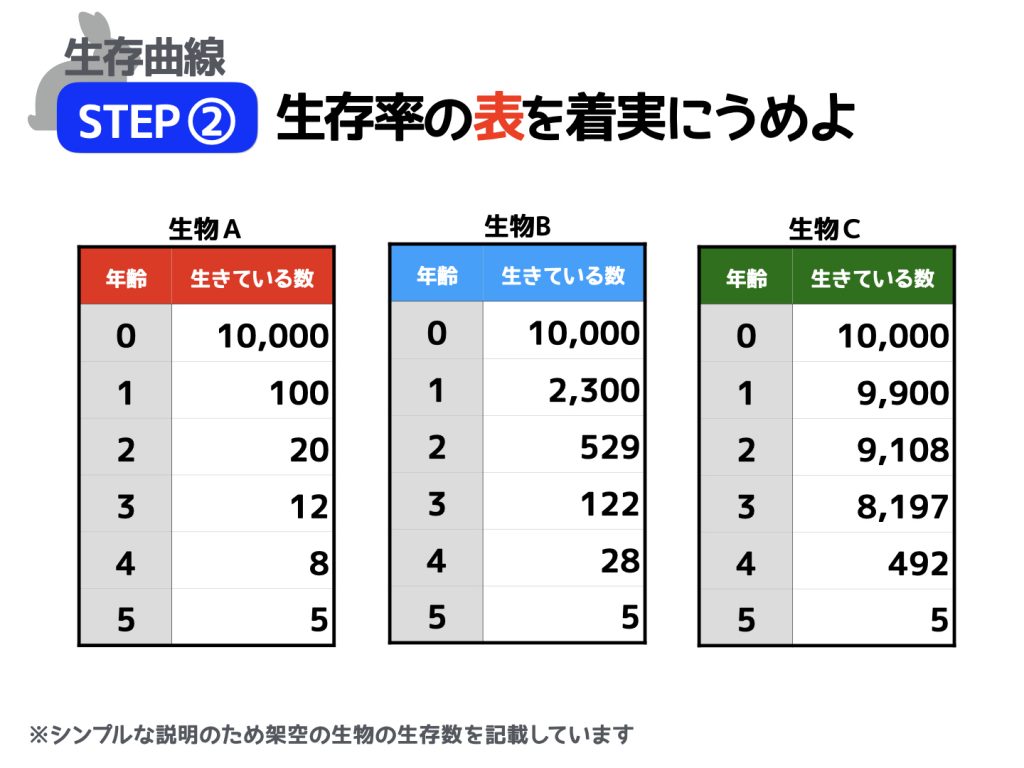
たとえば、次の表を見てみましょう。

これは3種類の生き物A～Cについて、それぞれの生きている数の推移を表したものです。

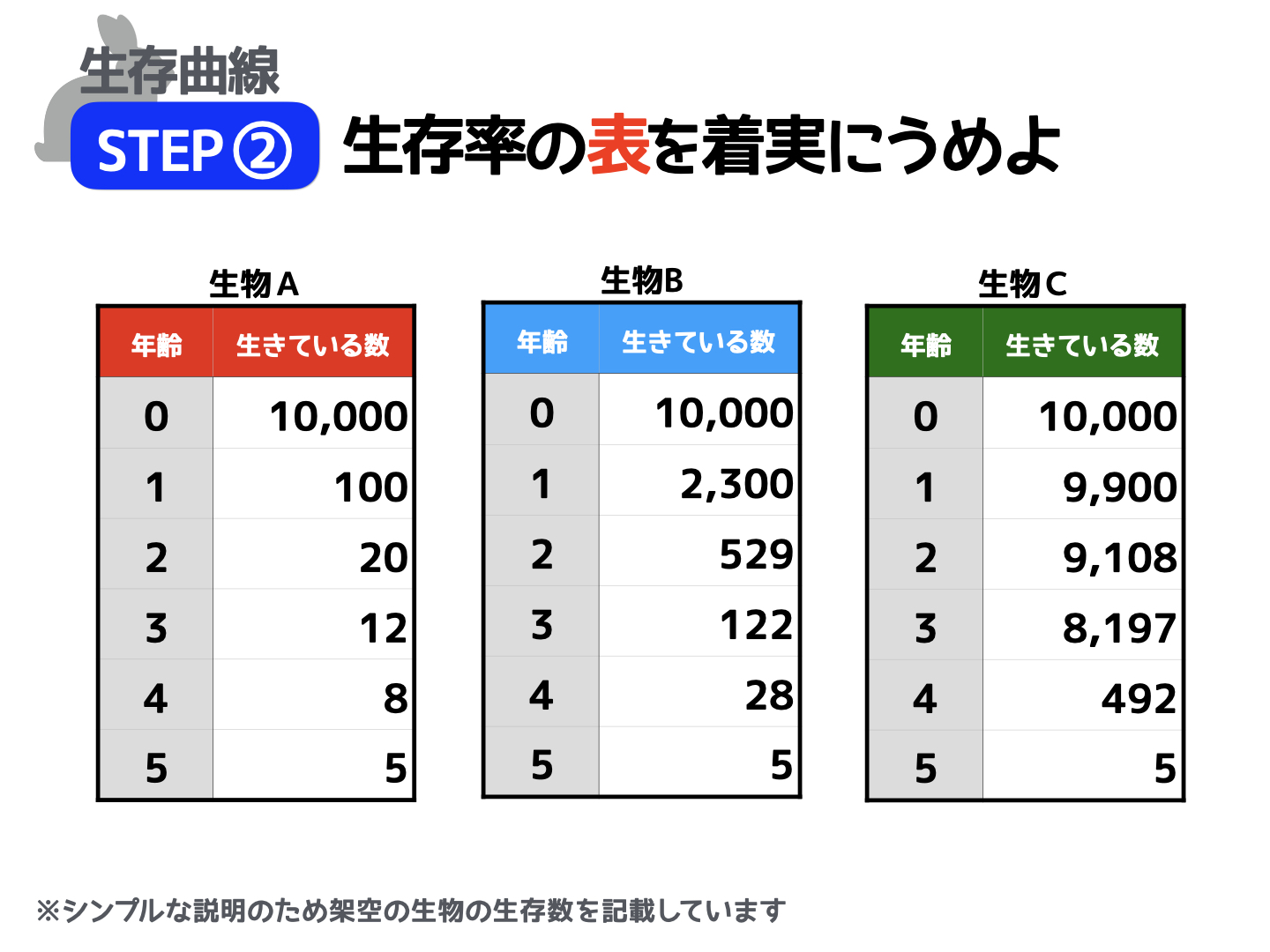
「生物Ａ」の表を見てみましょう。年齢＝0のときに10000匹いる、ということが読み取れますか？

年齢＝1になったときはどうでしょう？ 数が一気に減って100匹しか生き残っていない、ということが読み取れればOKです。

「生物Ｃ」の場合には、生物Ａと同じく年齢＝0のときは10000匹残っていますが、年齢＝1でも9900匹が生き残っていることがわかりますね。

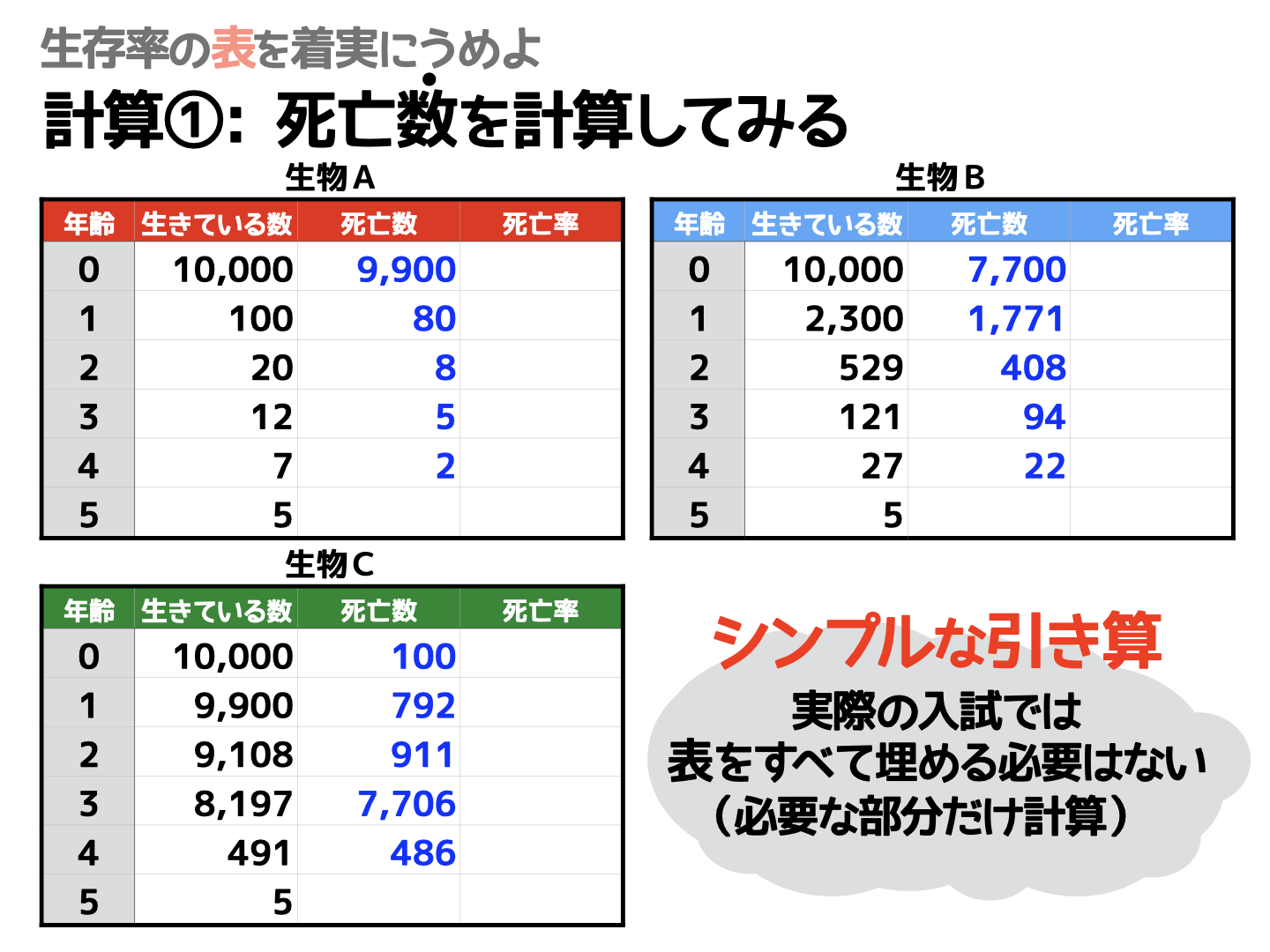
死亡数の計算

先ほどの「生存率の表」をもとに、死亡数（その年齢で死んでしまった数）も求めることができます。求め方は、超シンプルです。

たとえば「生物Ａ」は、年齢＝0では10000匹いたのに、年齢＝1では100匹になってしまいました。つまり、年齢＝0のあいだに9900匹が死んでしまったということがわかります。計算式は「10000－100」ですね。

同じように計算すると、以下のようにすべての表を埋めることができます。

死亡率の計算

次に、死亡率を計算してみましょう。

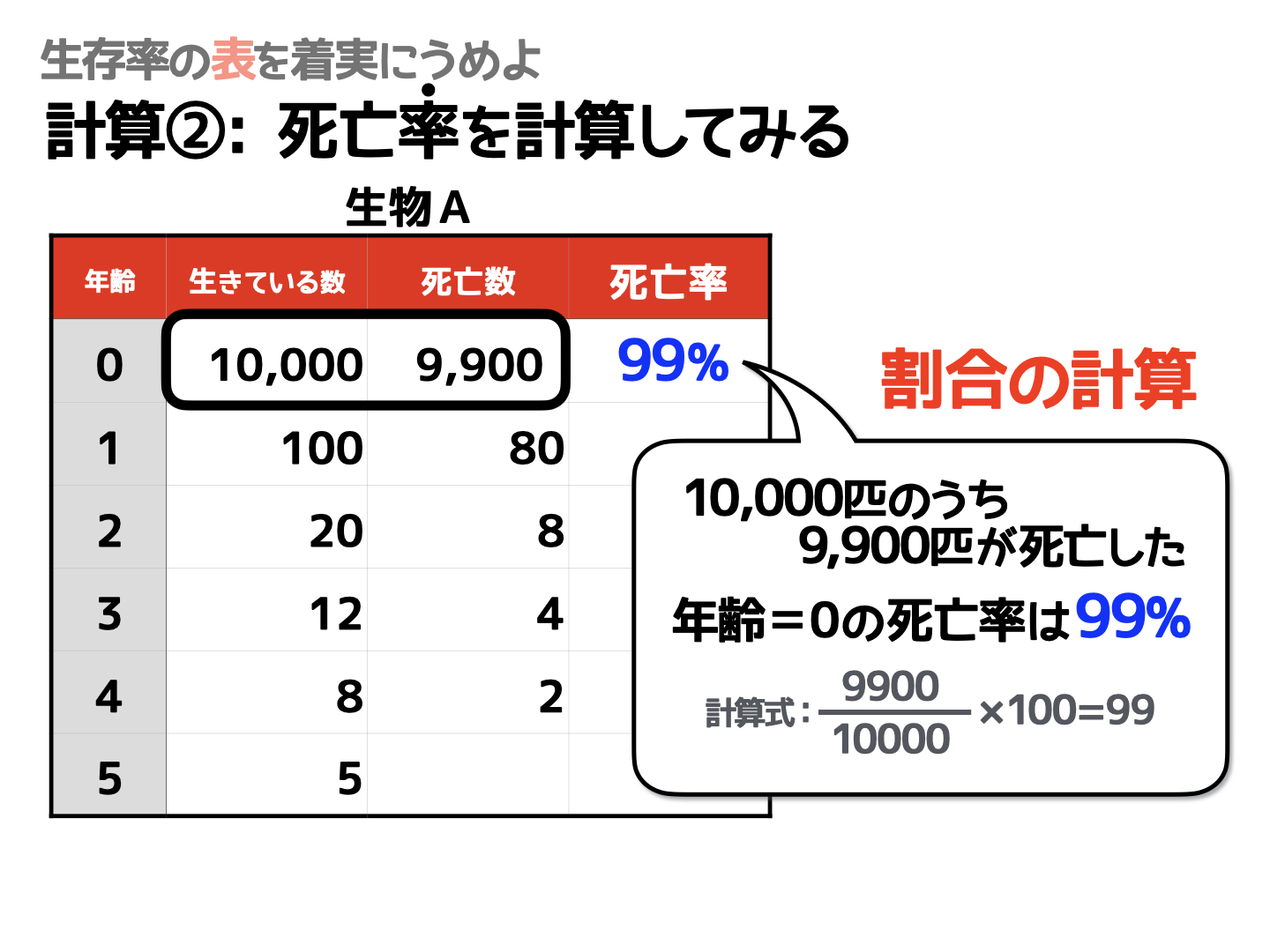
たとえば「生物Ａ」は10000匹のうち9900匹が死んでしまったので、死んでしまった割合は全体の99％です。「分子（死んでしまった数）／分母（もともと生きていた数）」で計算できますね。

死亡数と同じく、死亡率も計算によって表を埋めることができます。

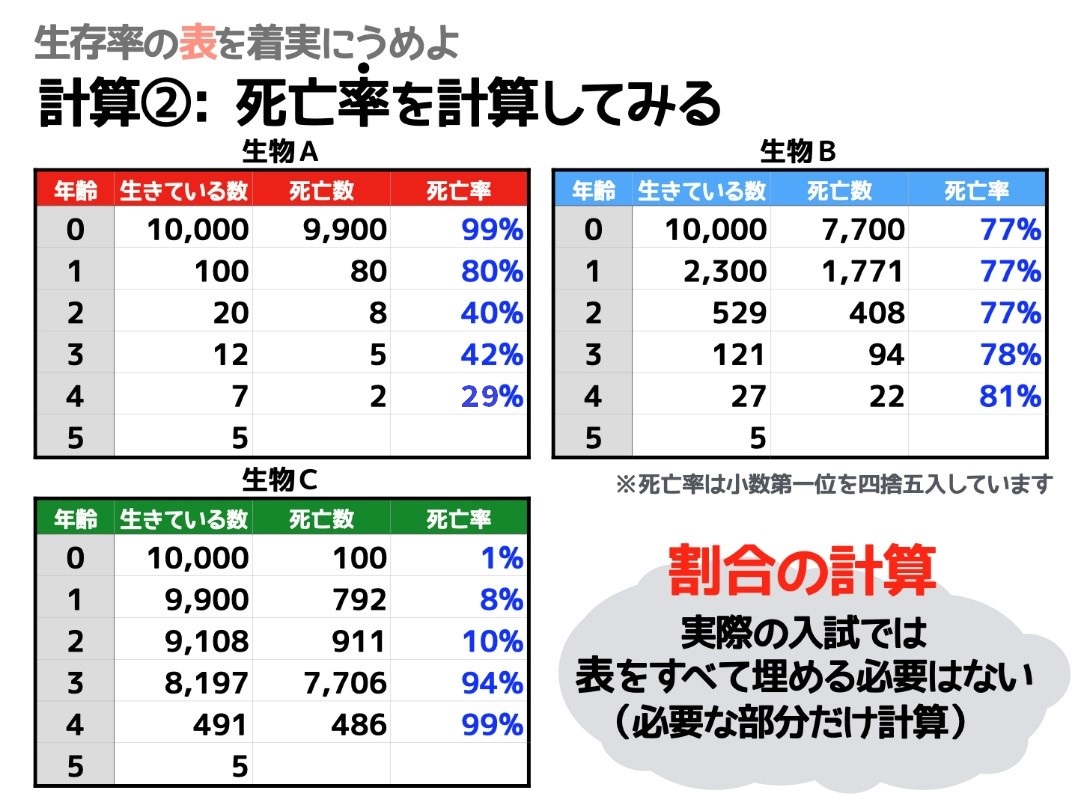
「表を埋める」というタイプの問題は、中学入試でも多く出題されています。

でも考え方は極めてシンプルなので、まずは次のふたつの計算をしっかりと押さえていれば大丈夫です。

STEP3：生存率のグラフを読み取ろう

生存率の表をしっかりと理解していれば、それについて描かれたグラフも難なく理解できそうですよね。

ところが、油断してはいけません。グラフについては、気をつけるべき“落とし穴”がいくつもあるからです。

まずは先ほど紹介した生存率の表をもとに、縦軸を「生き残る数」、横軸を「誕生から寿命までの年齢」としてグラフを描いてみましょう。ここまでは、とてもシンプルですね。

表の数値をグラフに落とし込んでいくと、以下のようなグラフができあがります。

たとえば「生物Ａ」は産まれてすぐに数が一気に減る様子が、「生物Ｃ」は寿命に近づくあたりから数が減っていく様子が読み取れますね。

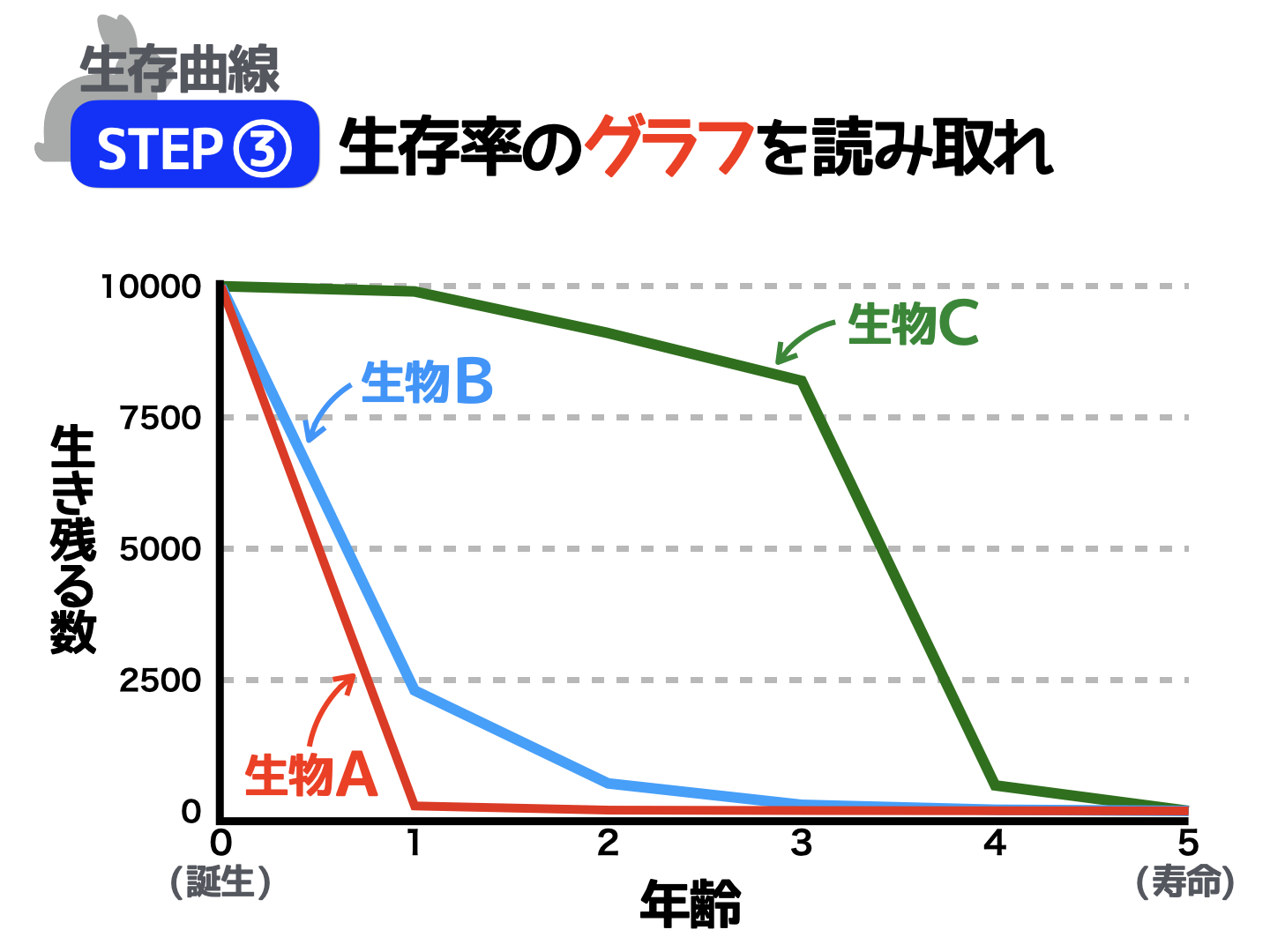
ここで、グラフについて注意したいことが2点あります。

縦軸の「ひと目盛り」が均等ではない場合がある

一般的に出題される生存曲線の縦軸を見てみると……、いつも見ている軸とはちょっと違うことに気づきます。

小学生が扱うグラフは縦軸の「ひと目盛り」がいつも同じ大きさですが、生存曲線では「ひと目盛り」の大きさが違う場合があるんです。

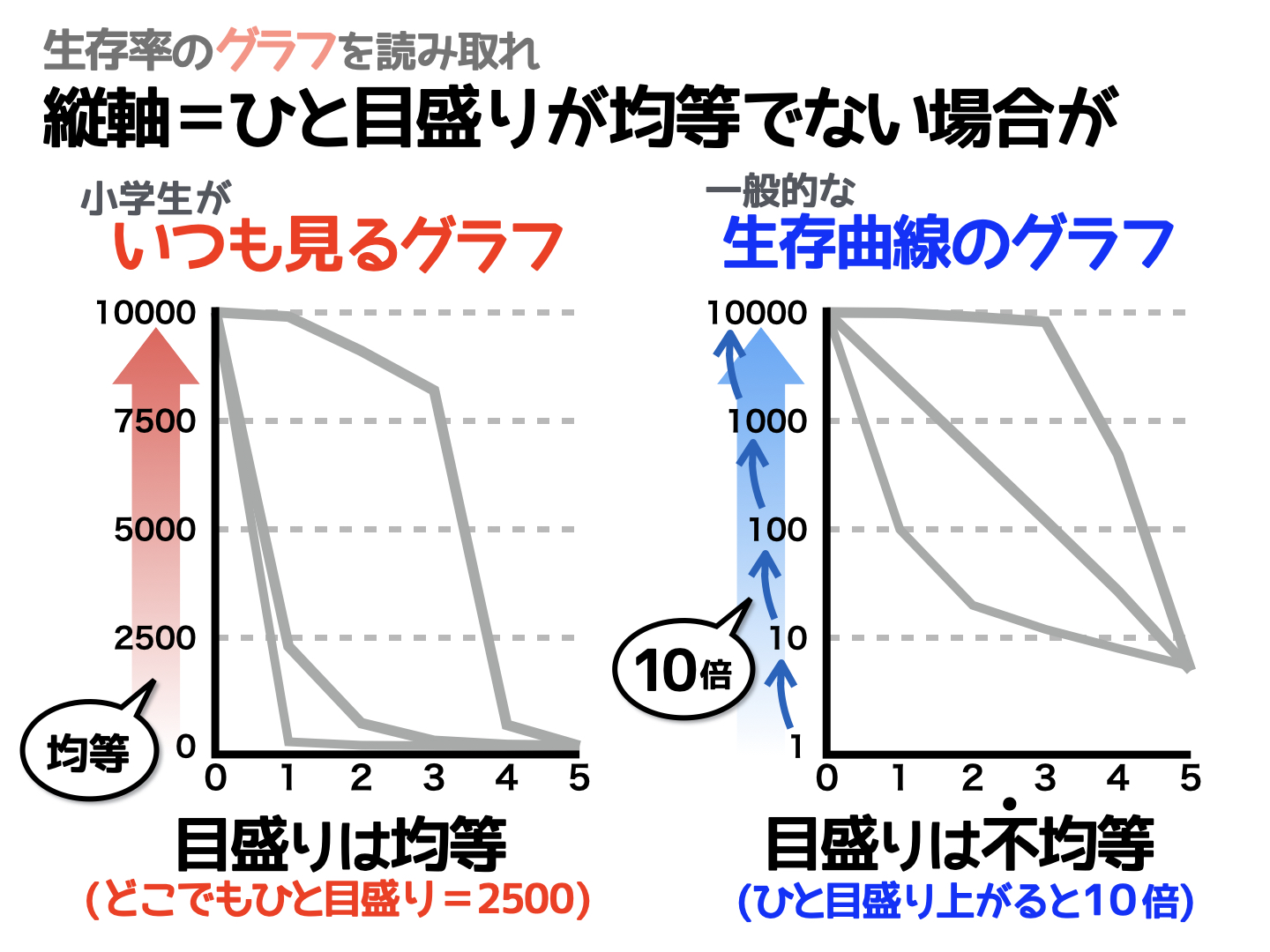
左のグラフは、小学生がよく見るグラフ。ひと目盛りは、どこを見ても2500ですよね。

右のグラフは、生存曲線でよく使われるグラフです。10の次は100、100の次は1000と、目盛りがひとつ増えるごとに10倍になっています。このような軸は「対数軸」といって、指数関数を扱うときなど、普通の目盛りだと変化量がわかりにくい場合に使われます。

ちなみに、小学生がいつも見ているグラフ（左のグラフ）の軸は「線形軸」といいます。

中学入試の段階では「こういう目盛りの取り方もあるんだ」ということを知っていればOKですが、問題文に目盛りの説明があってその目盛りの数字を埋めさせたり、グラフをプロットさせたり（描き入れたり）する問題が出題されたこともあるので、知識としては押さえておきましょう。

横軸は「相対年齢」で示されている

縦軸だけでなく、横軸にも注意したいことがあります。

それは、横軸が「相対年齢」で示されているということです。

ステップ3で、生物Ａ～Ｃの異なる生物の生存率を示したグラフを見ましたが、グラフを見る限り、どの生物も「年齢＝5」のときにほとんどが死亡していますよね。

これは、どういうことでしょうか？

たとえば「シャケ」のような魚類は、産まれて間もないうちにその多くがほかの生き物に食べられてしまいます。実際、その寿命は3〜7年程度といわれていますが、親に守られながら育つ「ニホンザル」の寿命は25年ほどです。

このように、寿命が異なる生物の生存曲線を同じグラフ内で比較できるように、グラフ上では横軸を「実年齢」ではなく「相対年齢」にしているんですね。

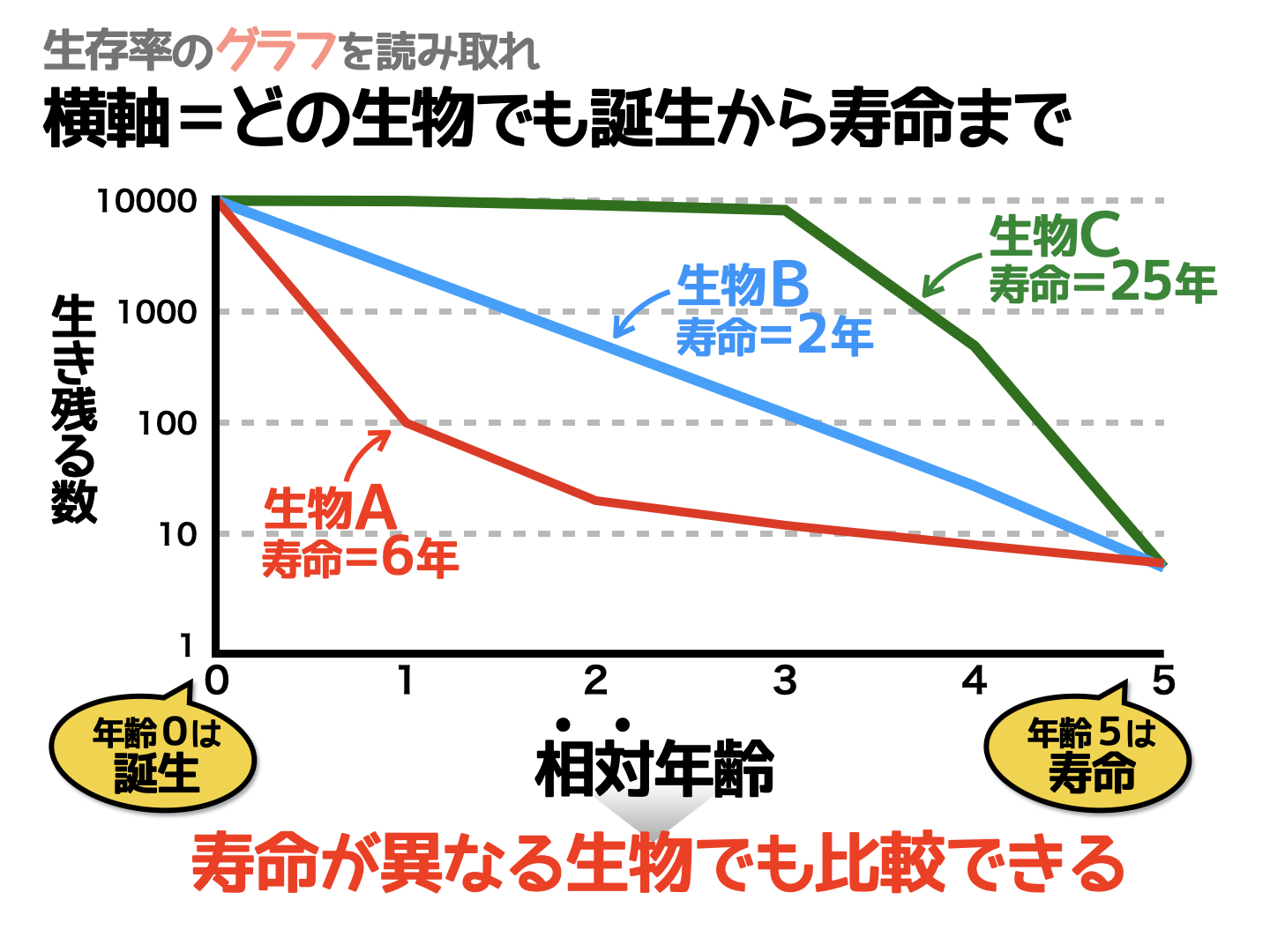
寿命が25歳のニホンザルであれば、「年齢＝5」は25歳です。すると年齢＝1では5歳、年齢＝2では10歳……ということが読み取れますね。

相対年齢の具体的な知識を入試で問われることはあまりないので、上記で説明したようなことが理解できていれば十分でしょう。

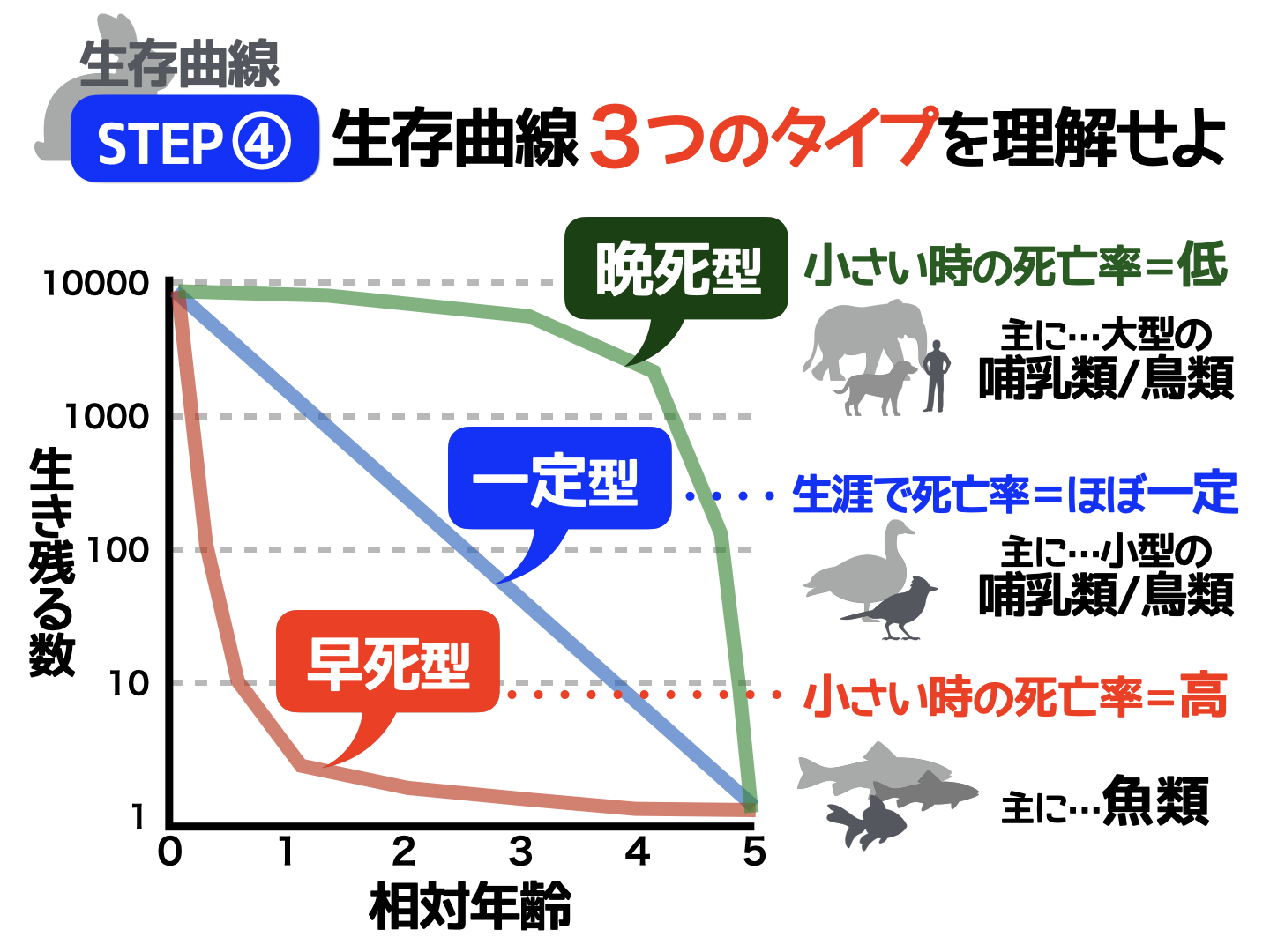
STEP4：生存曲線の3つのタイプを理解しよう！

ここまで生存曲線を見てきたなかで、それぞれの曲線が「3つのタイプ」に分けられることに気づきましたか？

タイプ［1］晩死型 ―― 小さいときの死亡率が低い

晩死型は、猿などの大きな哺乳類によく見られるタイプです。一度に多くの子供を産まず、小さいときの死亡率が低いことが特徴です。その多くが親に大切に育てられ、寿命に近くなるにつれて死亡率が高まっていきます。

中学入試では「晩死型にあてはまる生物を選ばせる」といった問題も出題されています。

たとえば、クジラ。

クジラは“大きな哺乳類“のため、晩死型に分類されますね。実際、どのクジラも親に守られて育ち、寿命に近づくにつれてその多くが死亡します。　

タイプ［2］一定型 ―― 生涯を通して死亡率がほぼ一定

一定型（※）は、誕生から寿命まで、ほぼ同じ死亡率で推移する生物に見られるタイプです。小さいときも大きくなっても、さまざまな要因によって同じような死亡率になる生物がこのタイプに分類されます。

※一定型は「平均型」と呼ばれることもあります

タイプ［3］早死型 ―― 小さいときの死亡率が高い

早死型は、（魚のように）一度にたくさんの卵を産むものの、卵のときや稚魚のときにその多くが食べられてしまう生物に見られるタイプです。小さいときの死亡率が高いので、生き残って寿命を迎える個体はごくわずかです。

STEP5：例外的な生物を押さえよう！

「生存曲線には3つのタイプがある」とお伝えしましたが、実は例外的なタイプがあります。

それが、大量に産まれる一方で、大量に生き残るタイプです。

応用的な知識ではありますが、中学入試で出題されたこともあるのでしっかりと押さえておきましょう。

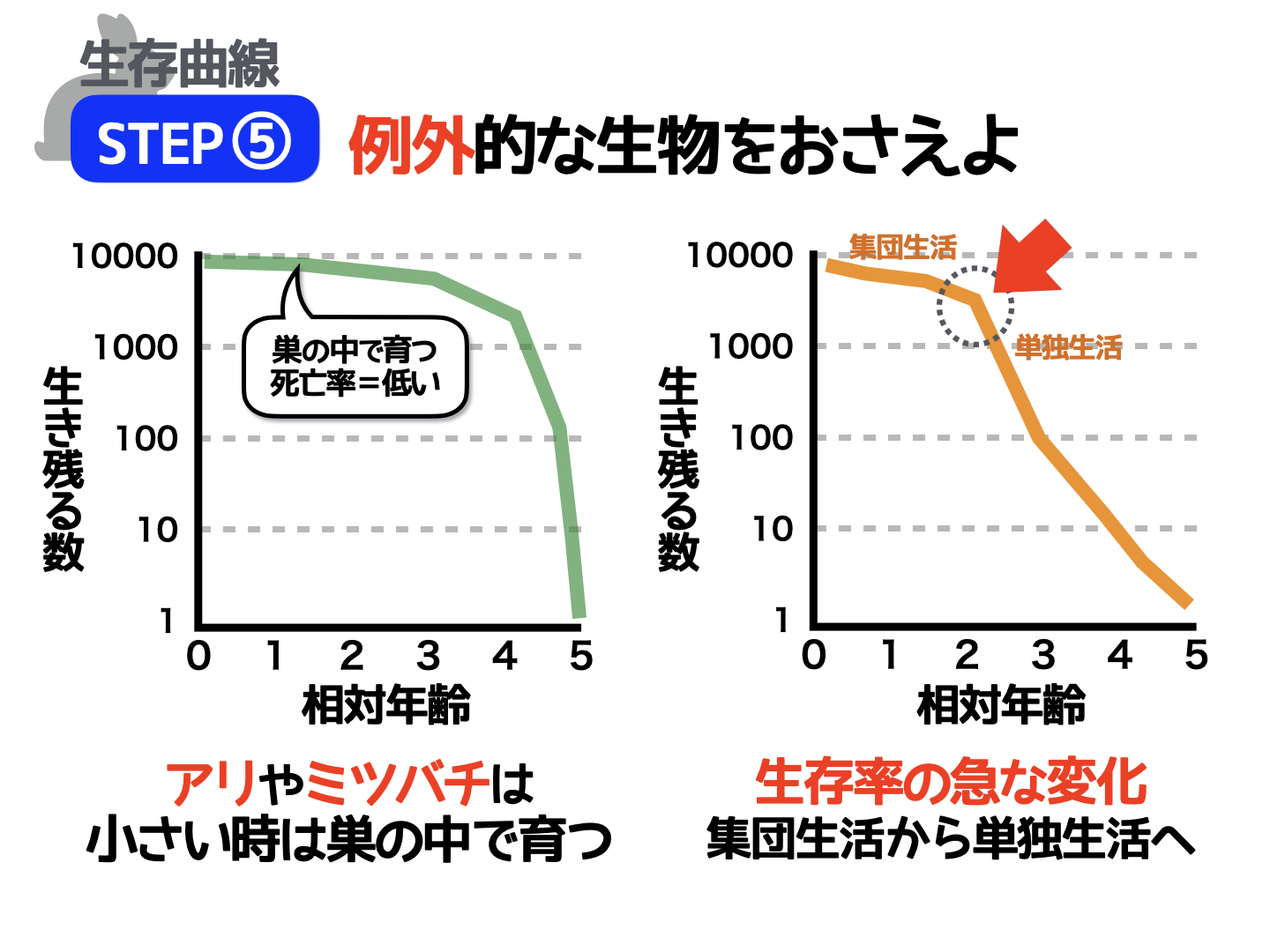
一度にたくさんの卵が誕生する生物は、そのほとんどが小さいうちに外敵に食べられてしまうことが一般的。ところが、巣のなかでたくさんの卵が大切に育てられることから、小さいときの生存率が高い生物も存在します。

それが、ミツバチやアリです。

たとえばミツバチは、卵のときも幼虫のときも、巣のなかでしっかりと守られながら育ちます。小さいときの死亡率がとても低いので、猿や人間と同じく「晩死型」に分類されています。

単独生活を始めた瞬間に何が起こる？

中学入試で出題された問題を見てみましょう。

答えは、死亡率が急に高くなる。

巣のなかは比較的安全かつ、外敵に食べられることもないので死亡率は高くありません。一方、巣の外に出た瞬間に外敵に襲われるようになります。そのため、死亡率が急に高くなるのです。

実際の入試問題では、生存曲線のグラフをもとに集団生活から単独生活になったときの年齢を推測させる問題も出題されています。そのため、まずは「単独生活を始めた瞬間に死亡率が高くなる」という知識を押さえておきたいですね。

まとめ

5つのステップを踏まえつつ、生存曲線について解説しました。

高校の生物で扱うような難しく感じられるテーマでも、中学入試では躊躇（ちゅうちょ）なく出題されます。しかし本質をしっかりと理解していれば、こうした難しいテーマの問題にも太刀打ちできるようになり、受験力向上にもつながります。

生存曲線については、今回紹介した5つのステップをもとに知識を固めつつ、実戦力をつけていきましょう！

※記事の内容は執筆時点のものです