相当算は割合を使うから難しい？ 線分図を描いて整理すればパズルのように解ける

中学受験算数でよく出るのが相当算です。相当算とは、ある数とその割合からもとにする数を求める特殊算です。今回は、子どもが相当算でつまずいたとき、保護者がどう教えるとよいかを紹介します。

相当算の前に割合を理解させる

相当算でつまずくのは、そもそも割合がわからないことに原因があります。保護者はまず、「割合とは何か？」を子どもに理解させましょう。

「割合とは何か？」を言葉で説明する

割合とは、ある数を1としたとき別の数がいくつになるかを表します。1とした数が「もとにする量」、別の数が「比べる量」です。もとにする量を100にすれば百分率、10にすれば歩合になります。

「10個は5個の2倍です」という場合の「2倍」も割合です。5個を1とすれば、10個は2になります。同じように考えれば、「6個は15個の\(\frac{2}{5}\)です」となることにも納得しやすいでしょう。15個が1ならば、15個よりも少ない6個は1をさらに小さくした数です。15個を3個ずつに5等分し、5つに分けたうちの2つ分が6個なので、割合は\(\frac{2}{5}\)になります。

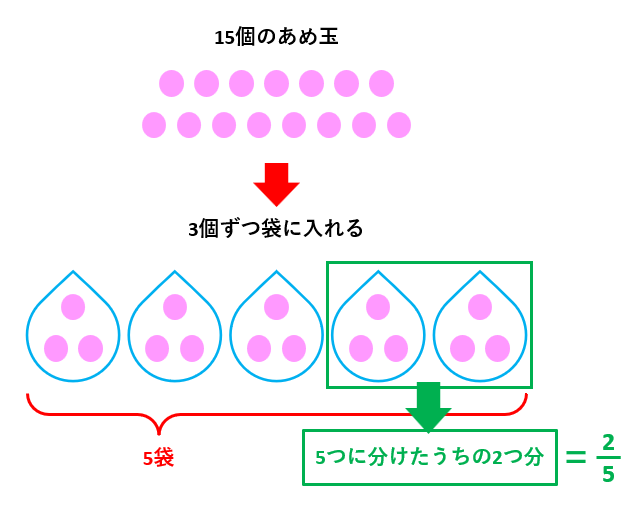
割合は整数で考えるとわかりやすい

「あめ玉15個の\(\frac{2}{5}\)は何個ですか」という問題は15×\(\frac{2}{5}\)＝6（個）と計算できます。しかし、分数のかけ算をするだけだと何をしているのかがよくわからず、子どもは「割合が苦手」をなかなか克服できません。そこで\(\frac{2}{5}\)を「5つに分けたうちの2つ分」と言いかえて、あめ玉15個を5袋に分けて、そのうちの2袋の個数を考えさせてみましょう。子どもは簡単に6個と答えを出せるはずです。

このように分数の割合を整数の比に言いかえると、子どもにとってハードルがぐっと低くなります。また、整数で考えることで分数計算が必要なくなり、分数特有の計算ミスも防げます。

相当算を線分図で考えさせる

相当算もあめ玉15個のように○を書いて数えても構いません。しかし、数が大きくなると○を書くのが大変です。そこで登場するのが線分図です。

もとにする量が変わる問題

【問1】はよく見る問題ですが、多くの中学受験生はつまずきがちです。つまずく原因の一つは、もとにする量が変わることです。

問題文の「1日目に全体の\(\frac{1}{3}\)」と「2日目に残りの\(\frac{3}{5}\)」から、1日目のもとにする量は全体ですが、2日目のもとにする量は（1日目に読んだページを除いた）残りだとわかります。子どもはもとにする量の変化に気づいていないことがあるので、保護者はまず「1日目と2日目で、もとにする量はそれぞれ何？」と子どもに聞いてみるとよいでしょう。

もとにする量の確認が終わったら、続いて子どもに「線分図を描いてみよう」と声かけします。子どもは線分図を描くことはわかっていても、どう描けばよいのかがわからずとまどいがちです。そんな子どもには保護者が「1日目と2日目があるから、とりあえず同じ長さの線を2本描くんだよ」と教えましょう。

2本の線を描いたら、そこに数字を書き込んでいきます。\(\frac{1}{3}\)は①と③に、\(\frac{3}{5}\)は□の3と□の5にしたのは、もとにする量が変わっているからです。この線分図にさらに情報を書き込んでいくと、下の図の通りです。

64ページは□の2なので、□の1は64÷2＝32（ページ）で、□の5は32×5＝160（ページ）です。さらに160ページは②なので、①は160÷2＝80（ページ）で、③は80＋160＝240（ページ）が答えです。線分図と整数の比を利用したら、パズルのように問題が解けました。

数を足したり引いたりする問題

【問2】は、割合から具体的な人数を足したり引いたりするので、【問1】よりも難しく感じる受験生が少なくありません。しかし、そんな受験生に対しても、保護者は「線分図を描いてみよう」と声かけすることから始めましょう。【問2】はクラスの全員を男子と女子に分けるので、一本の線を描くとわかりやすいはずです。

線分図の上に男子の比や人数を、下に女子の比や人数を書き込みました。男子の比は○、女子の比は□で囲って、それぞれを区別しました。特に注意すべきは、児童全員を必ず男子か女子のどちらかにすることです。子どもが15人を書いた後、保護者は9人を図の位置に書くよう促しましょう。

③と□の2はどちらも児童全員を表しているので、最小公倍数にそろえて△の6にしました。図のように△の比を書き込んでいくと、△の1は6人とわかります。児童全員は△の6なので、6×6＝36（人）が答えです。

相当算はパズルのように解ける

相当算では、割合を整数で考え、与えられた情報を線分図にまとめていくと、複雑な計算をせずに答えを出せます。子どもが相当算を「難しい」「わからない」と言っていたら、保護者は「慣れるとパズルのように解けておもしろいよ」と伝えるとよいでしょう。相当算ができるようになれば、他の受験生に差をつけられるはずです。

※記事の内容は執筆時点のものです