通過算は図を描けば簡単に解ける！ 旅人算との違いを理解して苦手意識を克服

中学受験算数の速さの応用問題に通過算があります。動くものに長さがあるため、普通の旅人算よりもやや複雑です。このような通過算を苦手とする中学受験生のために、図を使ってわかりやすく考え方を解説します。

通過算とはどのような問題か？

通過算とは、電車がトンネルや陸橋などを通過する問題です。2台の電車がすれ違ったり追い越したりするパターンもあります。

まずは、電車が電柱やトンネルといった「動かないもの」を通過する問題を考えましょう。

電車が電柱を通過する問題

通過算で電柱や人が登場する場合、電柱などの幅を考えません。図に電車を描くときは、先頭がとがった台形を描くと見やすくなります。これらをふまえて【問1】の図を描くと次の通りです。

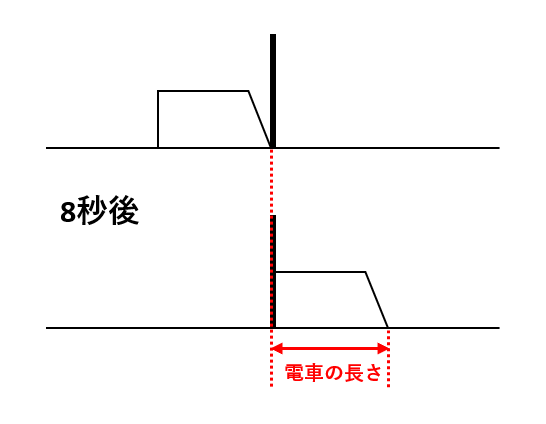
上の図と下の図（8秒後）を見比べるときは、電車の先頭か最後尾に注目します。今回は先頭に注目すると、先頭が8秒で電車の長さ分だけ移動したことがわかるでしょう。したがって、先頭が秒速25mで8秒走ると電車の長さになるので、電車の長さは25×8＝200（m）です。

電車がトンネルを通過する問題

【問1】との違いは、電車が通過するトンネルに1500mという長さがあることです。トンネルや陸橋を通過する問題では、これらの長さが問題を解く上での手掛かりになります。【問2】の図は次の通りです。

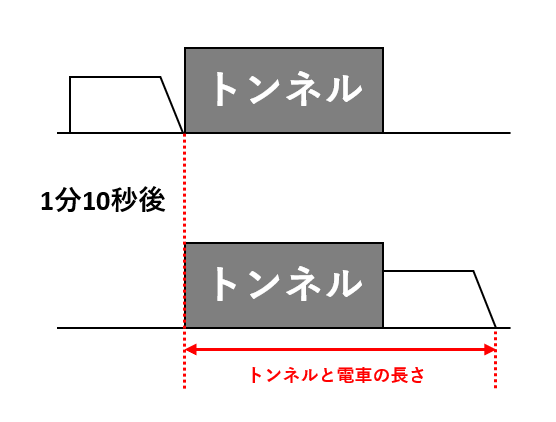
上の図と下の図（1分10秒後）で電車の先頭に注目すると、先頭は1分10秒（70秒）でトンネルと電車の長さ分だけ移動したことがわかります。したがって、先頭が秒速25mで70秒走るとトンネルと電車の長さの和になるので、その和は25×70＝1750（m）です。1750mからトンネルの長さ1500mを引いて、電車の長さ250mを求められました。

通過算と旅人算はどう違うか？

2台の電車がすれ違ったり追い越したりする通過算は、2人の人がすれ違ったり追い越したりする旅人算と考え方は同じです。しかし、旅人算は動くものに幅がないのに対して、通過算は幅（長さ）がある点に違いがあります。

すれ違いの問題を比較する

実際にすれ違いの問題で旅人算と通過算を比べてみましょう。

(1)はすれ違い（出会い）の旅人算です。太郎君と花子さんの距離は1分間で70＋50＝120（m）ずつ縮まります。したがって、2人は分速120mで2400mの距離を縮めていくと考えて、2400÷120＝20（分）が答えです。

(2)はすれ違いの通過算です。(1)とは違い、電車Xと電車Yがすれ違い始めてからすれ違い終わるまで時間がかかります。電車Xと電車Yに幅（長さ）があるからです。このことをふまえて図を描くと次の通りです。

すれ違い始めは、電車Xと電車Yの先頭同士が重なったときです。一方、すれ違い終わりは、最後尾同士が重なったときです。

また、すれ違い始めてからすれ違い終わるまでに、2台の電車の進んだ距離の和は、電車Xの長さと電車Yの長さの和になっています。2台の電車は秒速（25＋30）mで（150＋180）mの距離だけ離れたと考えて、（150＋180）÷（25＋30）＝330÷55＝6（秒）が答えです。

すれ違いの旅人算も通過算も速さの和を使っている点では同じですが、注目すべき距離が違っていることに注意しましょう。

追い越しの問題を比較する

追い越しの問題でも旅人算と通過算を比べてみましょう。

(1)は追い越しの旅人算です。弟が家を出てから10分後、弟と兄の距離は50×10＝500（m）離れました。この距離を兄は1分間で70－50＝20（m）ずつ縮めていくので、500÷20＝25（分）が答えです。

(2)は追い越しの通過算です。次のように図を描いてみました。

電車Xが電車Yに追いついてから追い越すまでに、2台の電車の先頭が進んだ距離の差が、電車Xの長さと電車Yの長さの和になっています。2台の電車の先頭は秒速（30－25）mで（200＋150）mの距離だけ走ったと考えて、（200＋150）÷（30－25）＝350÷5＝70（秒）が答えです。

通過算は図を描けば簡単に解ける

通過算も速さの応用問題である以上、旅人算などと考え方は同じです。図を描けば簡単に解けるので、受験生は諦めずにチャレンジしてみましょう。

※記事の内容は執筆時点のものです