分配算の解き方をわかりやすく解説！ 割合と比が出てくる特殊算も難しくない
多くの中学受験生が、割合の文章題として最初に出会うのが「分配算」です。分配算は、和と差だけで解ける和差算よりも複雑になりがちで、比の単元でも出てくるため、苦手とする受験生が少なくありません。そんな分配算の解き方をわかりやすく解説します。
分配算の基本
分配算の基本問題について、線分図を描く解き方と計算だけの解き方を紹介します。
分配算とはどのような特殊算か？
分配算では、あるものを分けたり配ったりするとき、その分け方・配り方から具体的な数量を求めます。似たような特殊算に和差算があります。和差算が和と差だけを使うのに対して、分配算では割合や比を使います。
割合を習いたての受験生は「分配算は難しい」と感じがちです。確かに、分配算を計算だけで処理しようとするとわかりにくいこともあるでしょう。しかし、線分図などを使って具体的な状況をイメージしながら考えれば、決して難しくありません。
分配算を線分図で解く
【問題1】63個のあめ玉を太郎君と次郎君で分けたところ、太郎君がもらったあめ玉の数は次郎君がもらったあめ玉の数の2倍よりも6個少なくなりました。太郎君がもらったあめ玉は何個ですか。
【問題1】を線分図で表すと以下の通りです。問題文の「6個少なくなりました」を点線で表しています。
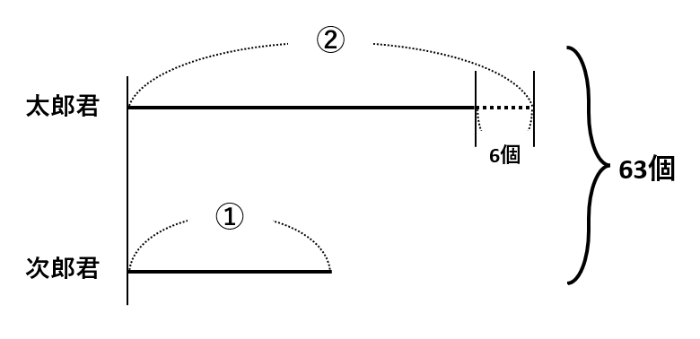
以下の図のように、太郎君のもらったあめ玉の個数と全体の個数にそれぞれ6個を加えると、②＋①＝③＝69とわかります。
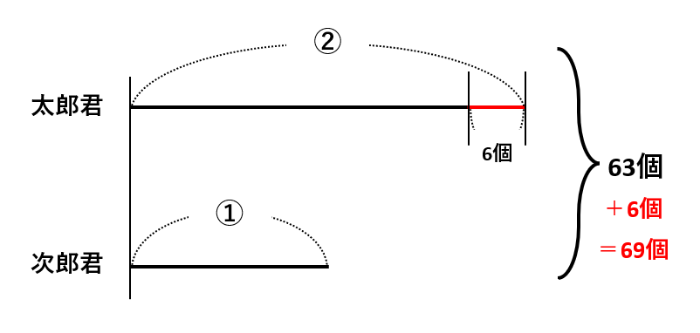
したがって、①＝23なので、太郎君がもらったあめ玉の個数は、②－6＝23×2－6＝40（個）です。
分配算を計算で解く
【問題1】を、線分図を描かずに計算だけで解いてみましょう。
次郎君がもらったあめ玉を①個とすると、太郎君がもらったあめ玉は（②－6）個です。したがって、（②－6）＋①＝63となり、③＝69から①＝23なので、②－6＝23×2－6＝40（個）です。
分配算を解くときは、割合を表す数字と具体的な金額を表す数字を区別することが大切です。今回は、割合を表す数字を○で囲みました。
分配算の応用
さまざまな分配算の解き方を紹介します。線分図などを使って情報を整理することが大切です。
3人で分ける問題
【問題2】兄、姉、弟の3人でお金を出し合って、15000円のプレゼントを買います。兄は姉よりも2100円多く出し、姉は弟の2倍よりも300円少なく出しました。兄が出したのはいくらですか。
【問題2】のように3人で分ける問題でも、2人で分ける問題と同じく線分図を描きましょう。
以下の図のように、兄が出したお金と合計金額からそれぞれ2100円を引き、兄が出したお金、姉が出したお金、合計金額にそれぞれ300円を加えると、②＋②＋①＝⑤＝13500とわかります。
したがって、①＝2700なので、兄が出したお金は、②－300＋2100＝2700×2＋1800＝7200（円）です。
計算で解く場合は、弟が出したお金を①とすると簡単でしょう。姉が出したお金は②－300、兄が出したお金は（②－300）＋2100＝②＋1800なので、3人の合計金額は（②＋1800）＋（②－300）＋①＝15000と表せます。⑤＋1500＝15000より①＝（15000－1500）÷5＝2700となり、兄が出したお金は、②－300＋2100＝2700×2＋1800＝7200（円）です。
はじめの数がわからない問題
【問題3】春子さんと夏子さんはそれぞれいくつかのおはじきを持っています。春子さんが夏子さんに12個あげると、2人のおはじきの数は同じになります。夏子さんが春子さんに7個あげると、春子さんのおはじきの数は夏子さんのおはじきの数の2倍になります。春子さんがはじめに持っていたおはじきは何個ですか。
【問題3】を線分図で表すと以下の通りです。
線分図を正確に描くと、②－①＝（12＋7）×2とわかるので①＝38です。したがって、春子さんがはじめに持っていたおはじきは②－7＝38×2－7＝69（個）です。
線分図を描くのが難しい場合は消去算で解くとよいでしょう。
春子さんと夏子さんがはじめに持っていたおはじきをそれぞれx個、y個とすると、以下の2つの式を作れます。
x－12＝y＋12 … ①
x＋7＝（y－7）×2 … ②
①よりx＝y＋24なので、これを②に代入してy＋24＋7＝（y－7）×2です。（y－7）×2＝y×2－14なので、y＋31＝y×2－14より、y＝45を求められました。したがって、春子さんがはじめに持っていたおはじきはx＝y＋24＝45＋24＝69（個）です。
分配算で割合と比に慣れる
分配算は割合や比に慣れるのに最適です。しかも、線分図を描いたり、計算力を磨いたりするといった、他の特殊算にも応用できるスキルも身に付きます。塾で単元の学習が終わった後も継続的に取り組むとよいでしょう。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます