
旅人算の基礎力|中学受験算数の基礎力を伸ばす#11
こんにちは!ドリるゼミ講師のさちです。
今回は旅人算の基礎力についてお届けします。
速さは中学受験算数の重要単元の1つですが、その中でもよく出題されるのが旅人算です。
旅人算で大切なのは
- 図を書く
- 距離の和や差に注目する
の2点です。
この記事で旅人算の基本の動きを確認しながら、基礎を固めていきましょう!
※速さの基本を確認したい方は
をご覧ください。
旅人算の4つの動きを確認しよう!
ここからは、旅人算の4つの動きを確認していきましょう!
お子さんに解いてもらう際は
- 図を書こう!
- 距離の和や差に注目してみてね
と声をかけてあげてください。
1. 出会う
まずは1つめは、出会いの旅人算です!
家と学校は900m離れています。
弟は分速60mで学校から家に向かって、兄は分速90mで家から学校に向かって同時に歩きだします。
(1)2人は1分あたり何m近づきますか。
(2)2人が出会うのは何分後ですか。
(1)2人の状況を図にしてみました。●が出発した時刻、△が1分後の2人の位置です。
同じ時刻にいる場所を同じマークで表すと分かりやすくなります。
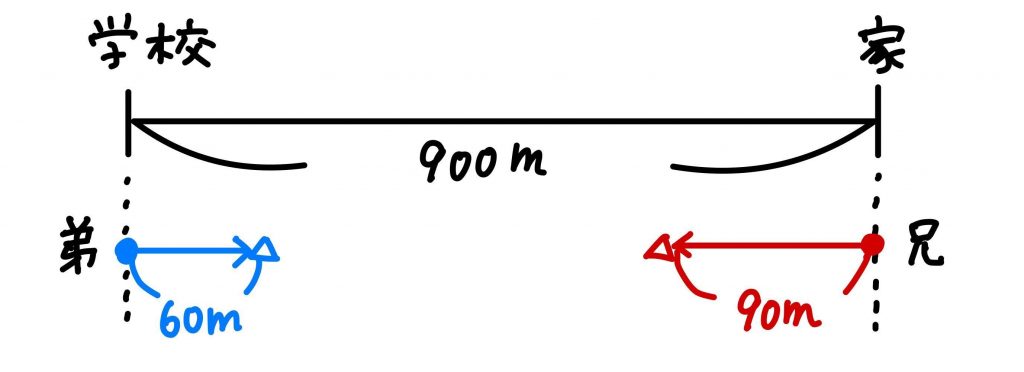
弟は1分あたり60m、兄は90m進むので、2人の距離は60+90=150mずつ近づいていきます。
答え.150m
(2)2人が出会ったときの図を書いてみましょう。
出発してから出会うまでの間に、2人は900m近づきます。
つまり、2人の進んだ距離の和が900mになることがわかりますね。
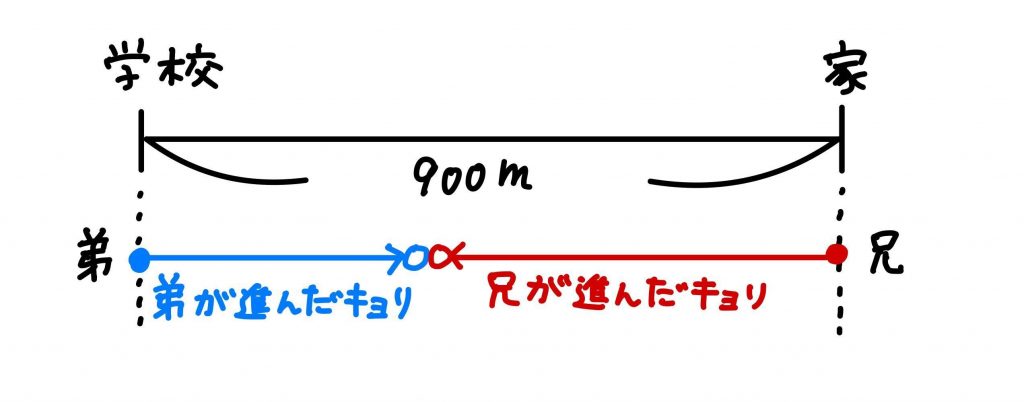
兄と弟は2人合わせて1分あたり150m進むので、
900m進むのは900÷150=6分後と分かります。
答え.6分後
2. 追いつく
続いて、追いつきの旅人算です!
弟は家から駅に向かって分速50mで歩きます。
弟が家から100m進んだところで兄が家を出発し、分速70mで弟を追いかけました。
(1)兄が歩き始めた後、2人は1分で何m近づきますか。
(2)兄が弟に追いつくのは、兄が歩き始めてから何分後ですか。
(1)兄が家を出発したとき、2人の距離は100m離れています。
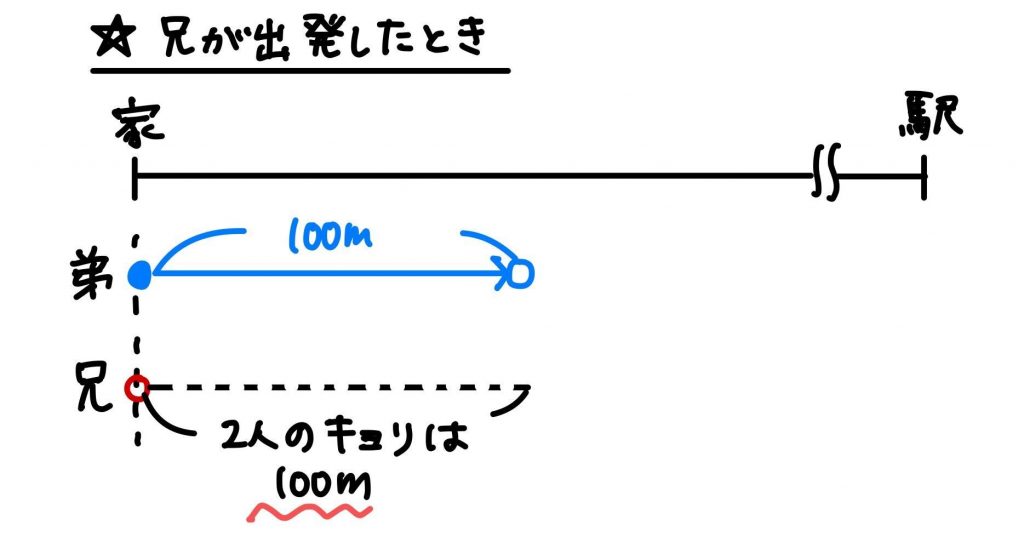
1分後、弟は家から100+50=150m、兄は家から70mのところまで進んでいるので
2人の距離は150-70=80mです。
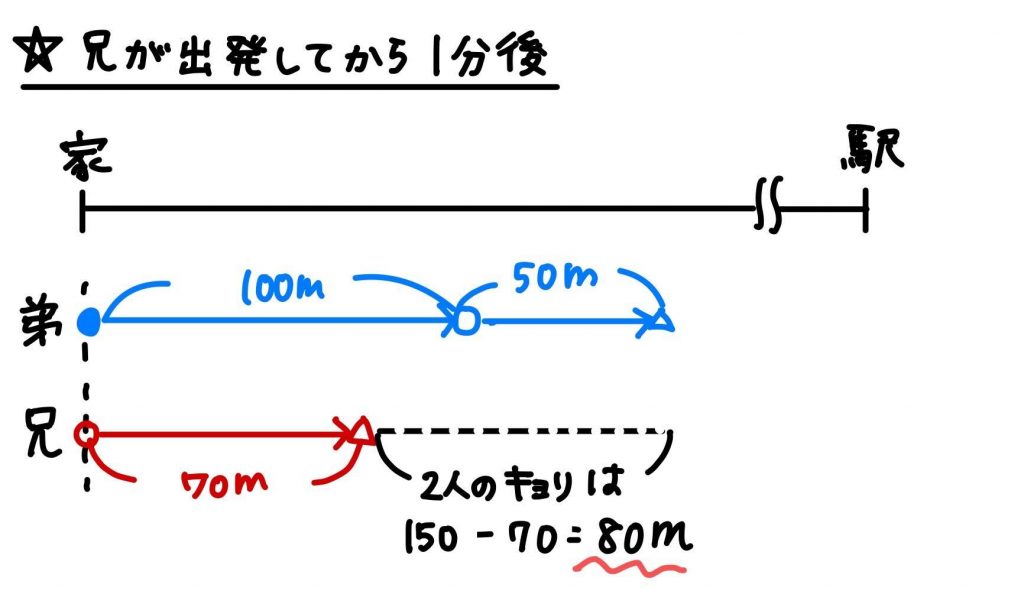
以上より、2人の距離は1分間で100-80=20mずつ近づいていくことが分かります。
(兄は1分で70m、弟は50m進むので、70-50=20mずつ近づくと考えてもOK)
答え.20m
(2)追いついたときの図を書いてみましょう。
追いつく=2人の距離がゼロになると分かります。
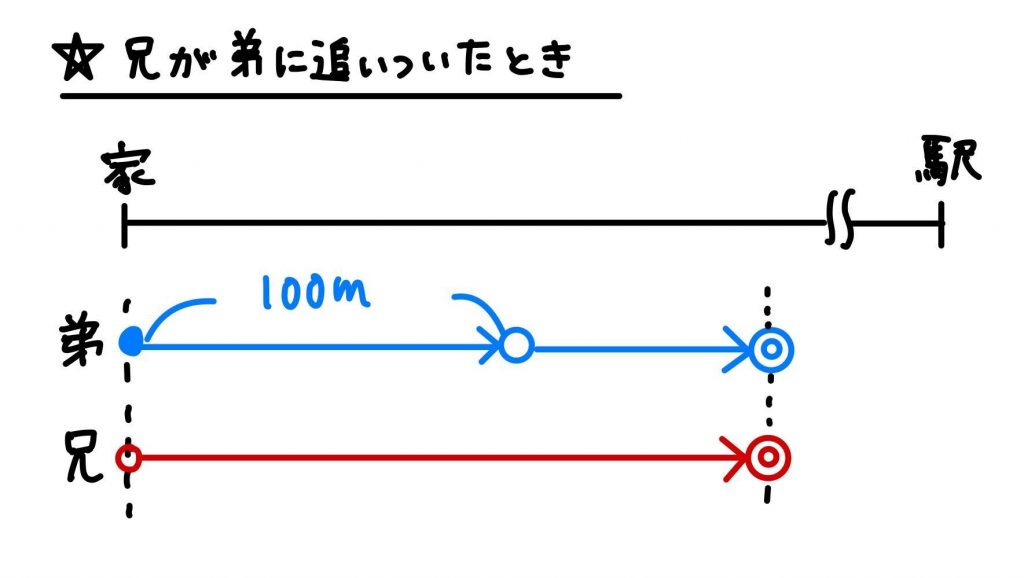
はじめ100m離れている2人が1分あたり20mずつ近づいていくので、
100÷20=5分後に追いつきます。
答え.5分後
3. 池の周りをまわる
3つめは池の周りをまわる旅人算です!
1周1200mの池の周りを1周する道があります。
姉は分速90mで、妹は分速60mでこの道の同じ地点から同時に出発します。
(1)姉と妹が反対方向に進むとき、2人が出会うのは何分後ですか。
(2)姉と妹が同じ方向に進むとき、姉が妹をはじめて追い越すのは出発してから何分後ですか。
(1)姉と妹が出会う時の図を書いてみましょう。
2人の進んだ距離の和が池の周り1周分(1200m)になっていますね。
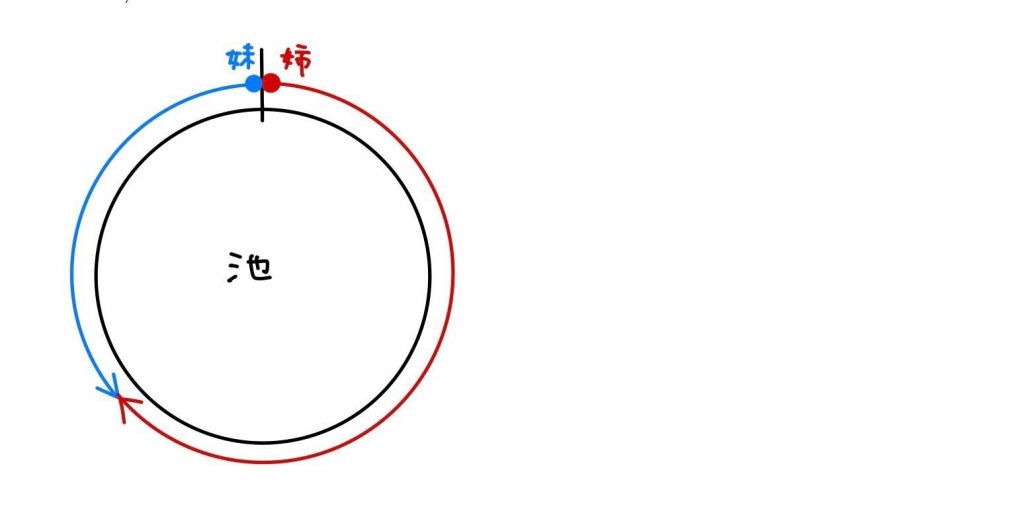
姉は1分で90m、妹は60m進むので、2人が進む距離の和は1分あたり90 + 60=150mです。
2人合わせて1200m進むのは、1200÷150=8分後ですね。
答え.8m
(2)姉が妹を初めて追い越すのは、妹が周回遅れになったとき。
その時の2人が進んだ距離の差は池の周り1周分(1200m)です。
こちらは図を書くのがなかなか難しいですね。イメージがつかめていればOKです。
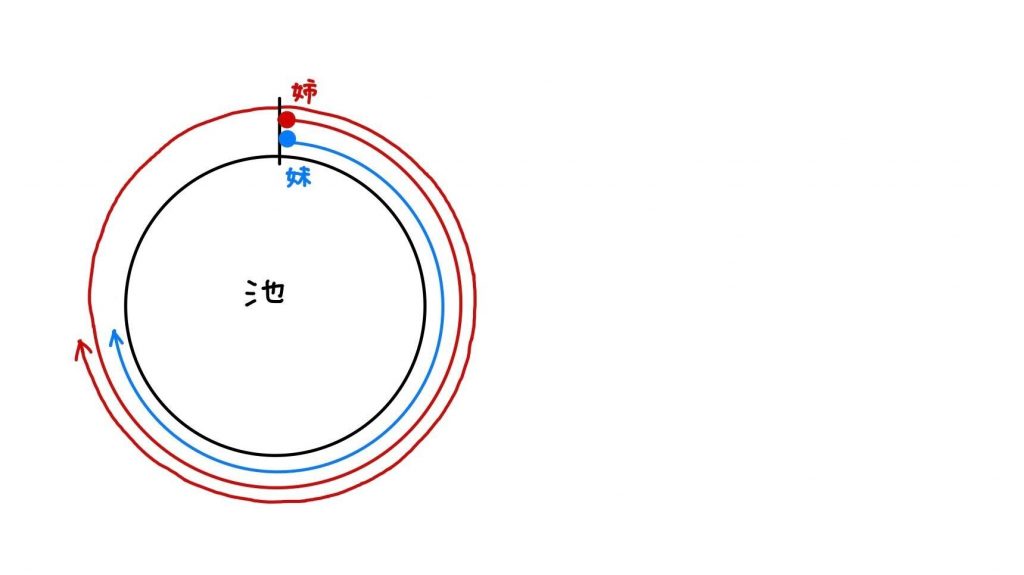
2人の距離は1分あたり90-60=30mずつ広がっていくので、
差が1200mになるまでには1200÷30=40分かかります。
答え.40分後
4. 往復する
最後は、往復する場合を確認しましょう。
720m離れたA地点とB地点の間を、兄は分速100mで、弟は分速80mで往復します。
2人はA地点を同時に出発し、B地点に付いたらすぐに折り返します。
兄と弟がすれ違うのは出発してから何分後ですか。
兄と弟がすれ違う時の図がこちらです。
すれちがうのは2人の進んだ距離の和が720×2=1440mになるときですね。
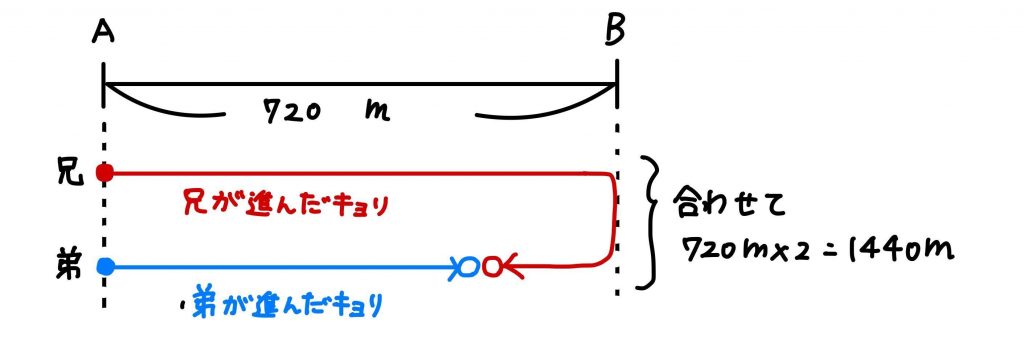
兄と弟は、2人合わせて1分で100+80=180m進むので
1440m進むまでには1440÷180=8分かかります
答え.8分後
応用問題に挑戦!
旅人算の基本が確認できたところで、一歩踏み込んだ問題にチャレンジしてみましょう!
(1)A地点とB地点は720m離れています。兄は分速100mでA地点からB地点に向かって、
弟は分速80mでB地点からA地点に向かって同時に歩き出し、AB間を往復します。
2人が2回目にすれ違うのは何分後ですか。
(2)姉は分速90mでA地点からB地点に向かって、妹は分速50mでB地点からA地点に向かって同時に出発します。
2人はAB間の真ん中より120m離れた地点ですれ違いました。
2人がすれ違ったのは出発してから何分後ですか。
(1)2回目にすれ違う時の図、書けましたか?
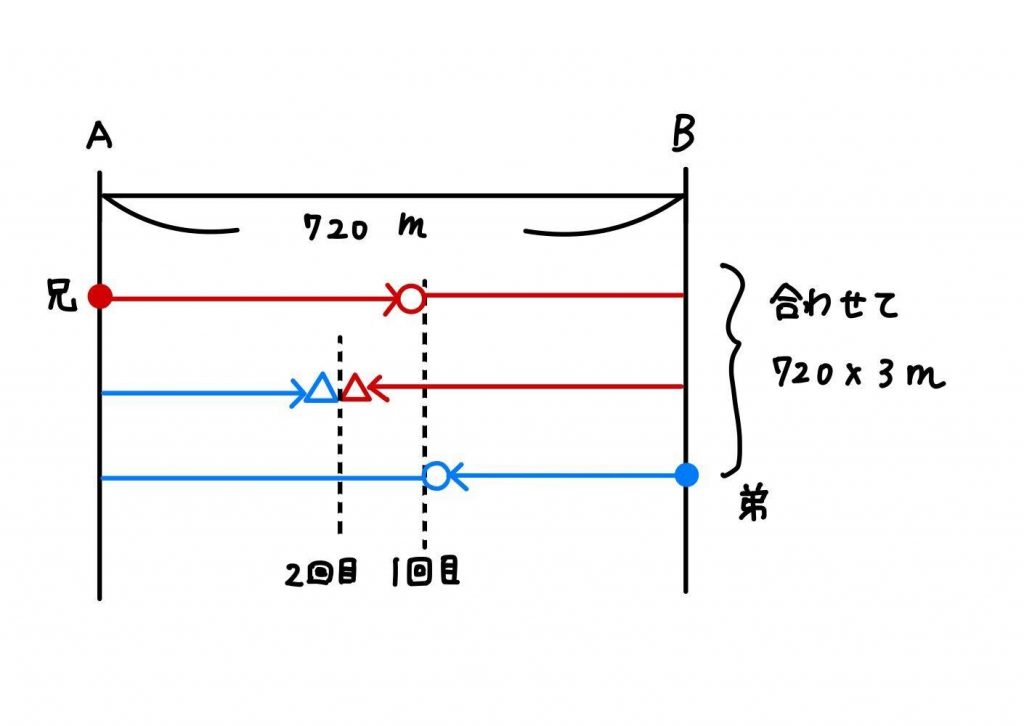
2回目にすれ違う時は2人が進んだ距離の和=AB間の距離×3となります。
2人合わせて1分で100+80=180m進むので、すれ違うのは720×3÷180=12分後です。
答え.12分後
(2)苦手な人が多い問題ですが、いかがだったでしょうか。
2人がAB間の真ん中より120m離れた地点ですれ違った時の図がこちらです。
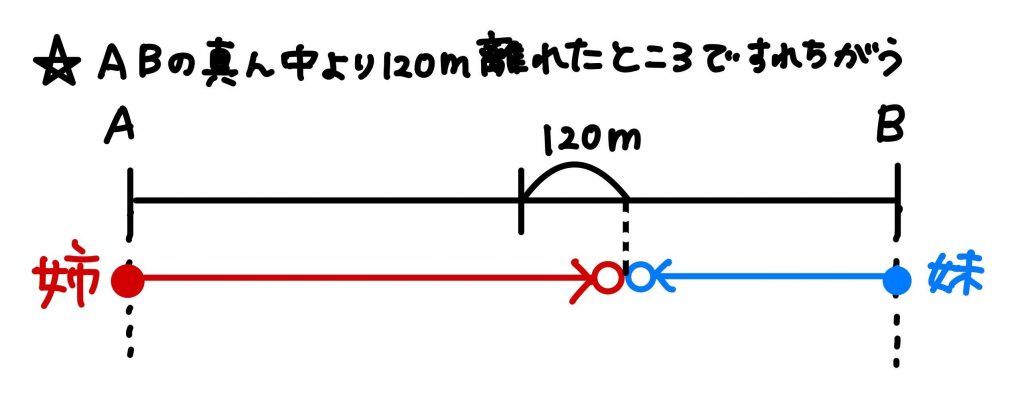
姉と妹が進んだ距離を比べるため、2人の進んだ距離を並べて書き直してみました。
すると、2人の距離の差=240mになっていることがわかりますね。
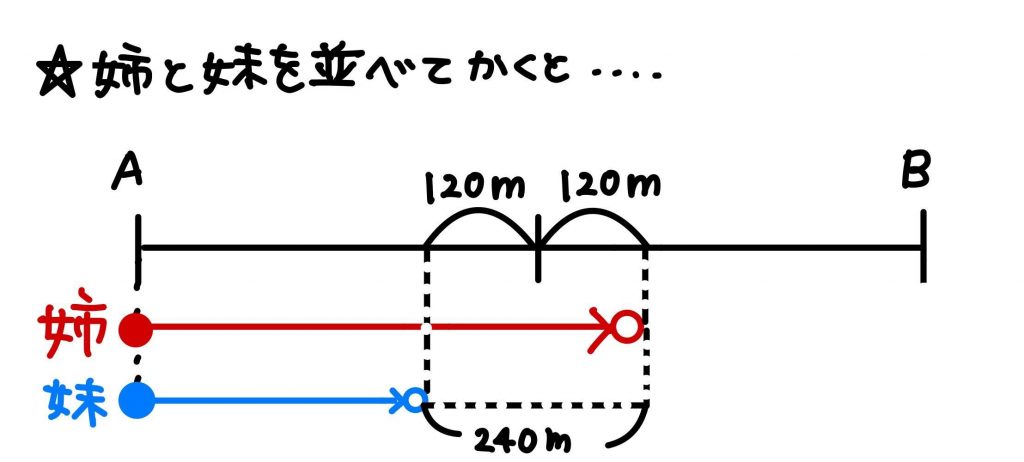
人が進む距離の差は1分間で90-50=40mずつ広がるので、240mの差ができるまでにかかる時間は
240÷40=6分
答え.6分後
まとめ
旅人算で大切なのは以下の2つです。
- 図を書く
問題文を読み進めながら、状況を図に書き起こしていきましょう。
同じ時刻にいる場所を同じマークで表すと分かりやすくなります。
- 距離の和や差に注目する
図が書けたら、その時の2人の距離の和や差を図から読み取りましょう。
図から読み取った距離の和や差と、1分あたりの距離の変化(=速さ)をもとに問題を解くことができます。
「2回目にすれ違う」など、状況設定が複雑な問題ほど、図を書いて状況を整理することが大切です。
「ドリる算数」に【旅人算の基礎力プリント】をご用意しました。
現在、無料でできます!(2023年11月時点)
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

