約数と倍数の基礎力｜中学受験算数の基礎力を伸ばす#10

こんにちは！ドリるゼミ講師のさちです。

現在、ドリるゼミの「計算くらぶ」にて、ご家庭での計算力アップをサポートさせていただいております。
今回からドリさん先生に変わって、私が算数の基礎力についてお伝えしていきますね。
どうよろしくお願いします！

突然ですが、お子さまは約数と倍数の単元は得意ですか？

約数と倍数の文章問題は、約数・倍数どちらを利用する問題なのかを見分けられないなど、苦手を感じている子が多い単元です。

この記事では、以下の2つのポイントに分けて約数・倍数の基礎をお伝えします。
1つずつ確認し、苦手をつぶしていきましょう！

①約数、倍数の求め方

まずは約数、倍数の基本を確認しましょう。

約数

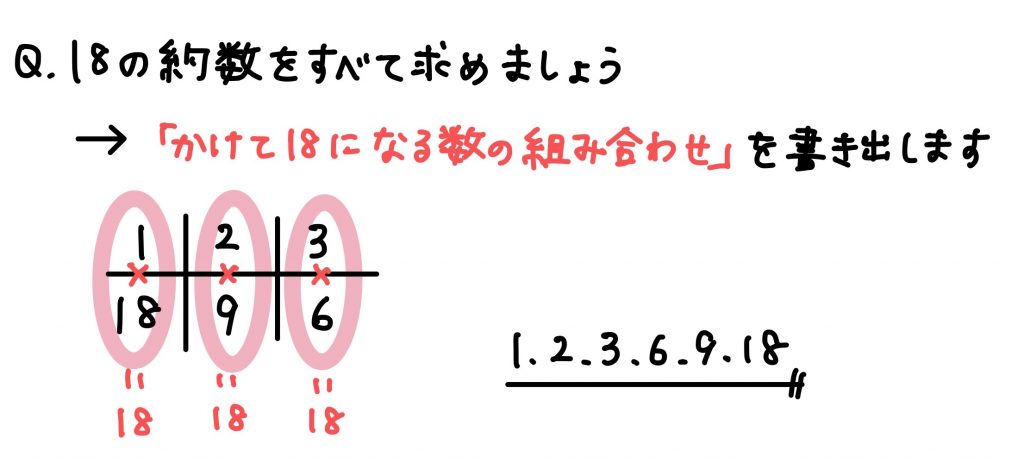
約数とは「ある数を割り切れる整数」のことです。

約数を求めるときは、ペアで書き出す癖をつけるともれなく書き出すことができます。

倍数

倍数とは「ある数を×1,×2,×3…してできる数」です。

×1を忘れやすいので注意しましょう。

②「あまりが出るわり算」の問題を解いてみよう

基本が確認できたところで、「あまりがでるわり算」にチャレンジしてみましょう！

まずはこちらの2問です。

お子様に考えてみてもらいましょう。

いかがでしたか？

• 求める部分を□として、わり算の式を作る
• □にあてはまるのはどんな数か書き出してみる

という手順で進めると、何をすべきかが見えてきますよ。

それでは、(1)の解説です。
求める数を□として式を立ててみると、「45の約数を求める問題なんだな」ということが見えてきます。

次に、(2)の解説です。

複雑そうに見えるかもしれませんが、実は(1)に1つ条件が加わっただけなので、同じ考え方で解くことができます。

続いて、こちらの2問にチャレンジです！

いかがでしたか？

この2問も先ほどと同じように

• 求める部分を□として、わり算の式を作る
• □にあてはまるのはどんな数か書き出してみる

という手順で進めることができます。

それでは(3)の解説です。
求める数を□として式を立ててみると、「5の倍数+4」を求める問題だと気付くことができます。

次に、(4)の解説です。

式を立てることで

• 5の倍数＋４
• 3の倍数＋２

のどちらにも当てはまる数を求める問題なんだな、と分かります。

解説は以上です。

どの問題も

• 問題文を読んで式を立てる
• あてはまる数字を書き出す
• 共通するものを見つける

という手順で答えを出せましたね。

パターンごとに解法を覚えると忘れた時に対応できなくなってしまいますが、この方法であればその心配はありません。

間違えてしまった人は、「ドリる算数」の【約数・倍数の基礎力プリント】でトレーニングしましょう。現在、無料でできます！（2023年10月時点）

まとめ

約数と倍数が苦手なお子さまは、次のポイントをチェックしましょう。

「あまりが出るわり算」の問題で説明した

• 問題文から式を起こしてその式をもとに考える
• 条件に合う数字を書き出す

という方法は、約数と倍数以外にも応用できます。

解き方が分からなくても諦めず手を動かす姿勢は、難問に立ち向かう力となり、入試本番でも大きな強みになるはずです。

約数・倍数の問題が、それに気づくきっかけになりますように。

※記事の内容は執筆時点のものです