「台形の面積が苦手」を克服する方法

台形の面積の公式と言えば『（上底＋下底）× 高さ ÷ 2 』ですよね。簡単といえば簡単な式ですが「覚えられない！」というお子さんもいるでしょう。しかし、そもそも公式をただ暗記するだけでは応用力が身につかず、平面図形が得意にはなりません。「なぜこの公式になるのか」を導き、理解することで、受験問題にも対応できる力を身につけましょう。

すべての面積の基本は長方形

長方形の面積が『 縦 × 横 』で求められることは、皆さんご存知でしょう。実は平面図形の面積を求めるさまざまな公式は、この長方形の面積の公式から導き出せるのです。では順番に求めていきましょう。

平行四辺形の面積の公式

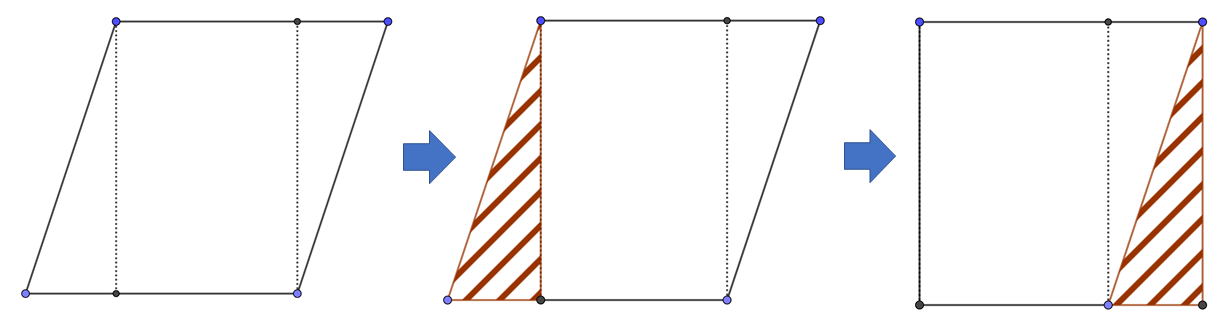
【図1】

まずは平行四辺形の面積の公式から求めていきましょう。

【図1】のように、平行四辺形を分割し、上手く組み合わせると長方形の面積になることがわかります。

結局、底辺がそのまま横の長さになり、高さが縦の長さになるので、『 底辺 × 高さ 』で面積が求められることがわかります。

三角形の面積の公式

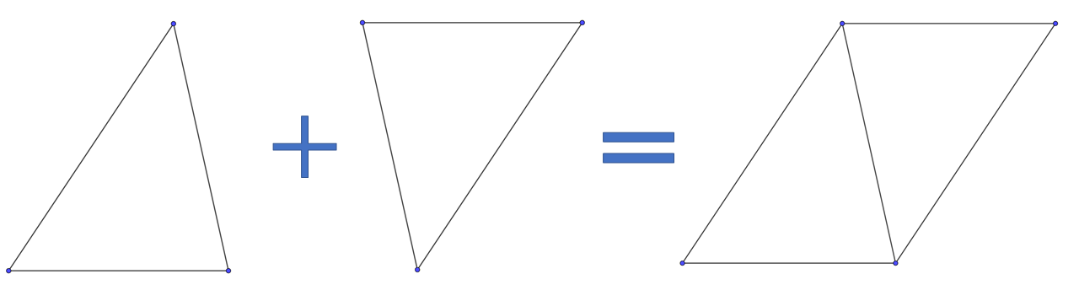
【図2】

当たり前のように使っている三角形の面積の公式。いわずと知れた『 底辺 × 高さ ÷ 2 』ですよね。これも導き出すことができます。

【図2】のように同じ形の三角形を用意して、組み合わせると平行四辺形になります。この平行四辺形の面積は、『 底辺 × 高さ 』で求められ、その半分が三角形の面積ということになります。

これで『 底辺 × 高さ ÷ 2 』であることが導けましたね。

台形の面積の公式を導こう

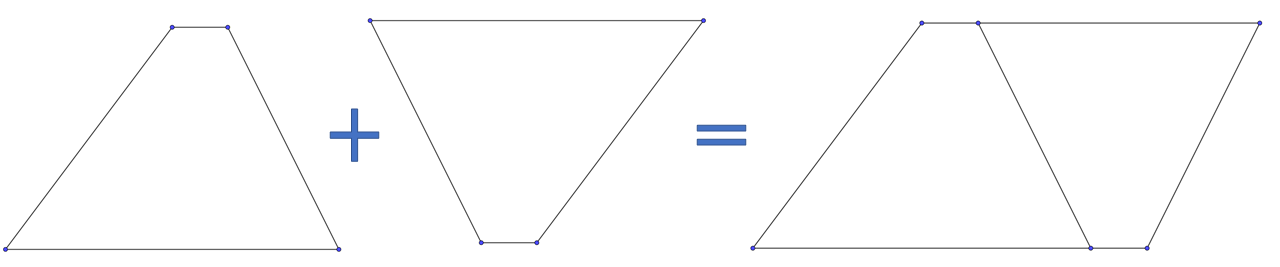
【図3】

いよいよ台形の面積の公式ですが、目新しいことはありません。

【図3】のように三角形同様、同じ台形を用意して組み合わせます。すると、底辺の長さが「 上底 ＋ 下底 」であるような平行四辺形ができますね。

これで、台形の面積が『（上底＋下底）× 高さ ÷ 2 』であることが導けました。

分割や組み合わせの過程が重要

これで、台形の面積の公式が求められたわけですが、なぜこんな導き方をしなければならないのかと思う人もいらっしゃるでしょう。意外かもしれませんが、この過程を知っているかどうかは、いろんな図形問題への応用力に大きく影響します。

対角線の長さが与えられた正方形の面積

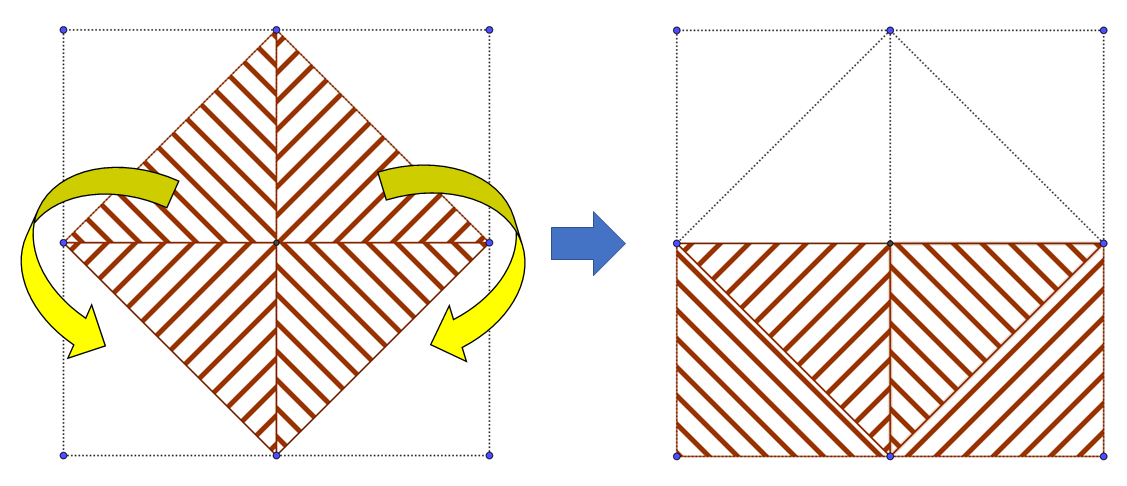
【図4】

例えば、対角線の長さが与えられた正方形の面積の求め方。

【図4】のように分割して、組み合わせると、対角線の長さを一辺の長さとする正方形の半分が、求めたい正方形の面積であることがわかります。

つまり、『 対角線 × 対角線 ÷ 2 』で面積が求められるということです。

このように平面図形を分割したり、組み合わせたりする発想があると、応用問題にも対応できます。

公式を関連づけて理解しよう

バラバラな知識として捉えていた平面図形の面積に関する公式も、一度長方形の面積から導けることを知ると、それぞれ関連づけて整理できるようになります。このように、集めた知識を体系的に整理することは、効率よく記憶を定着させることにもつながります。ただ公式を暗記するのではなく「なぜそうなるのか」を考えて、算数を楽しく理解していきましょう！

※記事の内容は執筆時点のものです