「水量の変化」の基礎力|中学受験算数の基礎力を伸ばす#13
こんにちは!さちです。
突然ですが、お子さまは「水量の変化」に関する問題は得意ですか?
- 容器に入っている水の体積や深さを求める
- 容器に円柱や角柱を沈めた時の水の深さの変化を求める
- 水を入れた容器を傾けてこぼれた水の量を求める
など、中学受験算数では、水に関する問題がよく出題されます。
比や仕事算などとからめて出題されることも多いので、そのような問題に取り組む前に基礎を確認しておきましょう。
この記事では、「水量の変化」の基礎力について、以下の3つに分けてお伝えします。
- 体積と水量の基本
- 視点を変えてみよう
- 容器に角柱をいれると…?
1. 体積と水量の基本
まずは基本事項のおさらいです!
次の問題をお子さまに解いてもらってください。
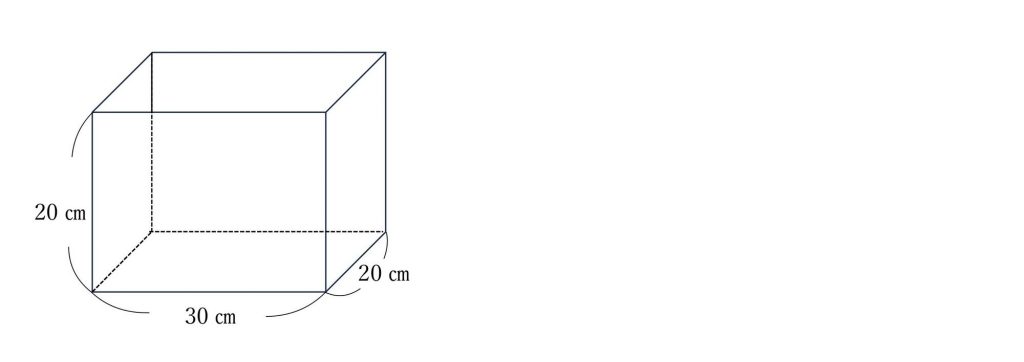
下のような直方体の容器があります。
(1)この容器の容積は何Lですか。
(2)この容器に18dLの水を入れると、水の深さは何㎝になりますか。
では、解説です。
(1)容積は底面積×高さで求められます。
底面積は20×30=600㎠、高さは20cmなので
容積は600×20=12000(㎤)と計算できました。
次に単位をLに変換します。
1000㎤=1000mL=1Lなので、
12000㎤=12L と分かります。
答え 12 L
答え 12L
(2)18dL=1800mL=1800㎤なので、水の深さを□cmとすると次の式が立てられます。
600×□=1800
□=1800÷600=3
答え 3 cm
ポイントは
- 水量=底面積×高さ
- 単位の換算(L・dL・mL⇔㎤)
です!
まずはここをしっかり押さえておきましょう。
体積の単位変換は、「ドリる算数」の体積の単位変換 で練習できます!
2. 視点を変えてみよう
次の問題です。
以下の問題を解いてみてください。
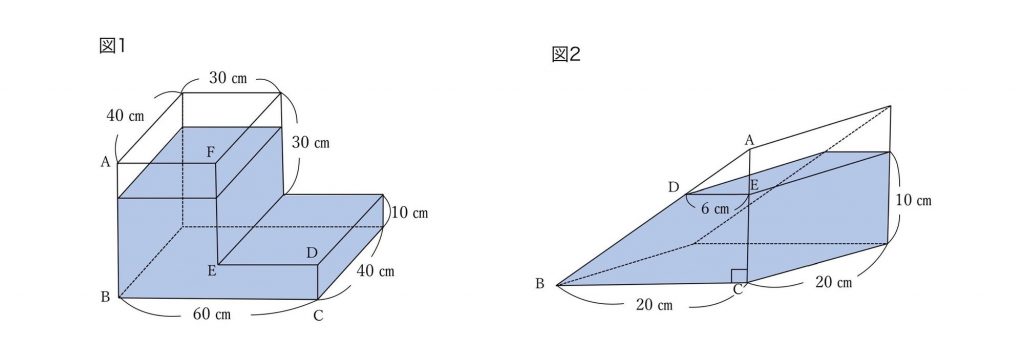
① 図1のような直方体を組み合わせた容器に、48Lの水が入っています。
容器にふたをして面ABCDEFがゆかにつくように置くと、水の深さは何cmになりますか。
② 図2は三角柱を横に倒した容器に10cmの深さまで水を入れた様子です。
入っている水の体積は何㎤ですか。
それでは答えです。
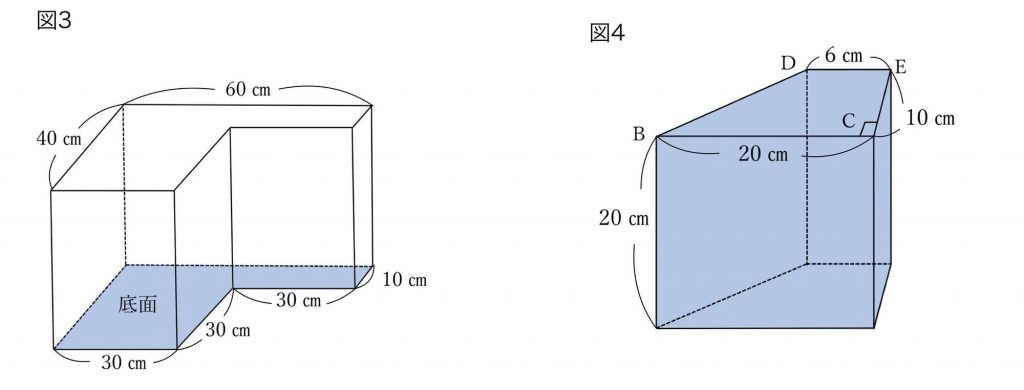
① 面ABCDEFがゆかにつくように置くと図3のようになります。
この立体の底面積は40×60-30×30=1500(㎠)です。
48L=48000㎤の水が入っているので、水の深さを□cmとすると次の式が立てられます。
1500×□=48000
□=48000÷1500=32
答え 32 cm
② 水が入っている部分を面DBCEが上になるように置きかえると、
図4のように「底面が台形の四角柱」と考えることができます。
この立体の底面積は(6+20)×10÷2=130(㎠)、高さは20㎝なので、水の量は
130×20=2600
答え 2600 ㎤
ポイントは
- 初めの図では側面になっている面を底面だと考える
です!
「底面=下になっている面」とは限りません。
どの面でも、その面を下にすると底面になります。
視点を変えて「別の面を底面と考える」という発想を持っておきましょう!
3. 容器に角柱をいれると…?
最後にこちらの問題にチャレンジしてみましょう!
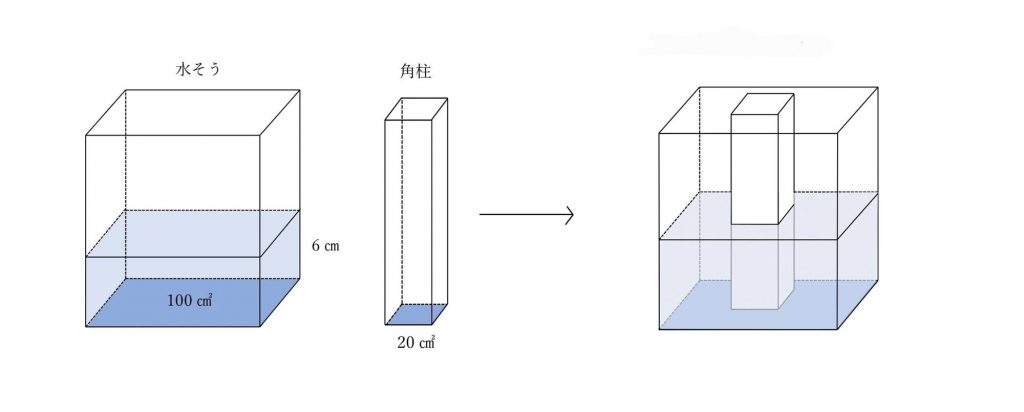
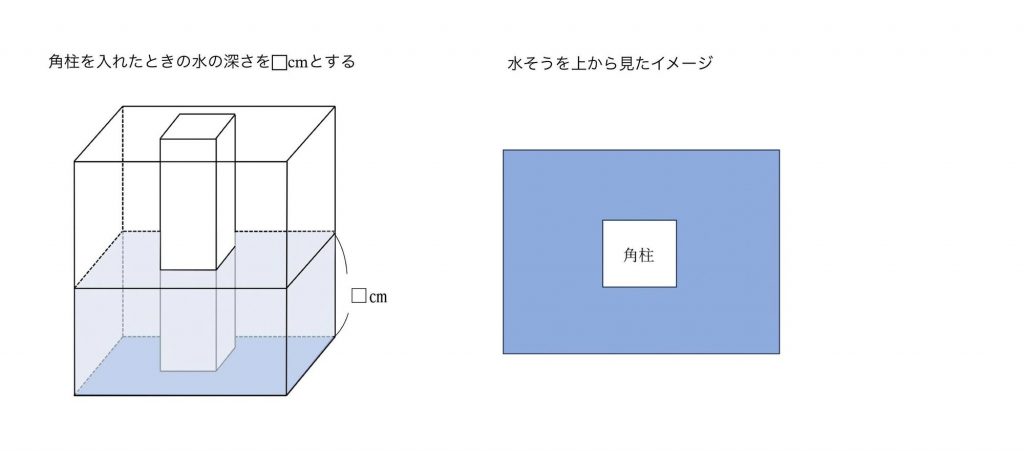
底面積が100㎠の水そうに、6cmの深さまで水が入っています。
底面積が20㎠の角柱を水そうの底につくまで入れると、下の図のようになりました。
このときの水の深さは何㎝ですか。
それでは、解答です。
水そうに入っている水の量は
100×6=600(㎤)
また、角柱を入れたあとに水そうを上から見ると、下の図のようになるので
水が入っている部分の底面積は
100-20=80(㎠)
角柱を入れる前後で水の量は変わらないので、深さを□cmとすると次の式が立てられます。
80×□=600
□=600÷80=7.5
答え 7.5 cm
いかがでしたか?
難しそうに見えますが、水量=底面積×高さという基本の考え方を使って解くことができました。
まとめ
「水量の変化」が苦手なお子さまは以下のポイントをチェックしましょう。
-
基本は「底面積×高さ」です。迷ったときはここに立ち返りましょう!
-
下になっている面=底面とは限りません。「側面を下にする」という視点を持ちましょう!
- 角柱を立てる問題では底面積の変化に注目してみましょう。底面積がどう変わるかが分かれば、あとは底面積×高さで問題を解くことができます。
以上です。
「水量の変化」の問題が得意になりますように!
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます