複雑な図形の面積の求め方5選！ 分割・移動・等積変形などのパターンを覚えよう
中学受験の算数では、図形の面積を求める問題が頻繁に出ます。しかも、問題となるのは、典型的な多角形や円ではなく、これらを組み合わせた図形であることが多いです。しかし、一見すると複雑な図形の面積も、ちょっとした工夫で簡単に求められることが少なくありません。今回は、中学受験生なら絶対に知っておかなければならない面積の求め方を整理して紹介します。
複雑な図形の面積の求め方は？
複雑な図形の面積を求めたい場合、基本的な図形をもとに考えるのがコツです。基本的な図形とは長方形・正方形・平行四辺形・ひし形・台形・三角形・円・おうぎ形です。これらの図形の面積を求める公式は以下の通りです。
- 長方形の面積＝縦×横
- 正方形の面積＝一辺×一辺
- 平行四辺形の面積＝底辺×高さ
- ひし形の面積＝対角線×対角線÷2
- 台形の面積＝（上底＋下底）×高さ÷2
- 三角形の面積＝底辺×高さ÷2
- 円の面積＝半径×半径×円周率
- おうぎ形の面積＝半径×半径×円周率×\(\frac{中心角}{360°}\)
以上の公式が使える基本的な図形を見つけたり、作ったりするため、必要に応じて複雑な図形を変形します。変形のパターンは限られているので、しっかり覚えて使いこなしましょう。
複雑な図形の面積の求め方5選
複雑な図形の面積を求める場合に役立つ変形のパターンを5つ紹介します。
1. 分割する
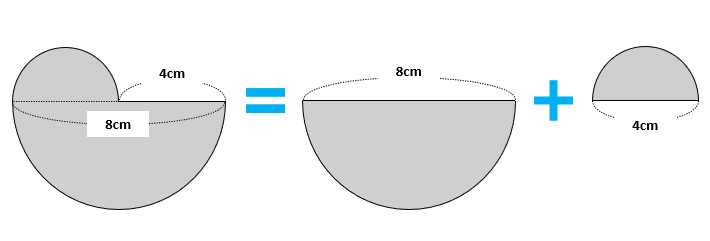
小学校の算数でも学ぶ考え方が、複雑な図形を基本的な図形に分割する方法です。下の図の一番左の図形は、直径が8cmの半円と、直径が4cmの半円に分割できます。したがって、一番左の図形の面積は4×4×3.14÷2＋2×2×3.14÷2＝（16＋4）×3.14÷2＝10×3.14＝31.4（cm\(^2\)）です。
2. 不要部分を引く
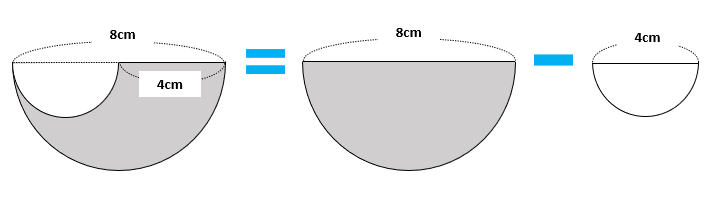
大きな図形から不要部分を引く面積の求め方も小学校の算数で学びます。下の図の一番左の図形は、直径が8cmの半円から、直径が4cmの半円を引けば、面積を求められます。したがって、一番左の図形の面積は4×4×3.14÷2－2×2×3.14÷2＝（16－4）×3.14÷2＝6×3.14＝18.84（cm\(^2\)）です。
3. 移動する
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます