【算数】いもづる算は「答えがたくさんある鶴亀算」―― 解き方のポイントを紹介

わが家の息子は、算数が超苦手でした。

その要因を探ってみると、解法そのものは理解できていても、いざ問題を読んだときにどの解法を使えば良いかわからなくなる……という状態だったんですね。

算数は試行錯誤を伴う問題も多いですが、基本問題に関しては問題を読んだ瞬間に解法がわかるものも少なくありません。

特に「文章題」はその代表格です。

今回は文章題のなかでも、答えがひとつに定まらない問題として知られる「いもづる算」の解き方を解説します。

いもづる算は鶴亀算のひとつの形

算数の世界では「鶴亀算」が有名ですが、一般に、算数で出題される鶴亀算は答えがひとつに決まります。

一方で、答えがひとつに決まらない（複数の答えがある）鶴亀算があります。

それが「いもづる算」と言われる問題です。

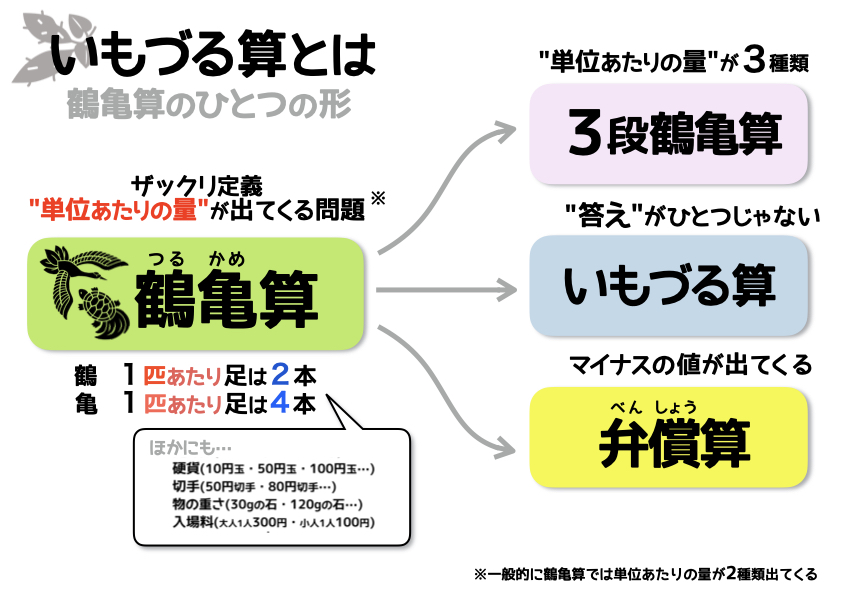
鶴亀算とは

鶴亀算をザックリと説明すると、“単位あたりの量”が出てくる算数の問題のこと。

では、単位あたりの量とは何でしょうか？

たとえば「動物の足の数」などですね。

この場合の単位あたりの量とは、“1匹”という単位あたりの数がきまっている量を指します。

単位あたりの量にはいろいろな種類があるので、お子さんと一緒に確認しましょう。

いもづる算の簡単な見分け方

問題文を読んで、どのようにして「いもづる算」であることを見分ければ良いのでしょうか？

ポイントは、問題文で明らかにされる3つの条件をチェックすることです。

この3つの条件がすべて問題文に書かれていれば、鶴亀算の解法を使って解けます。

そして、3つのうちどれか1つが欠けていたら「いもづる算」と判断できます。

条件は問題文にダイレクトに書かれていることもあれば、ちょっと遠回しに書かれていることもあります。

まずは、問題文に書かれている条件を落ち着いて拾っていきましょう。

問題文を見比べてみよう

鶴亀算の解法で解ける問題（答えがひとつに定まる問題）と、いもづる算の解法を使わないと解けない問題（答えがひとつに定まらない問題）を比べてみましょう。

上の図のように、問題文のなかに印をつけながらチェックしていくと、その問題が条件をどこまで出してくれているかわかります。

こうして実際に見比べてみると、鶴亀算といもづる算の違いをより深く理解できますね。

いもづる算を解く3つのステップ

それでは、いもづる算の具体的な解き方を解説します。

いもづる算は、シンプルな「3つのステップ」で解くことができます。

表を書くことで法則性がわかり、まさに「いもづる式」に次々と答えが出てきます。これが「いもづる算」と呼ばれる由来と言われています。

STEP1: 式を立てる

最初は「式を立てる」ステップです。

まずは、問題文を読みながら式を立てます（親御さんにとっては、中学で学ぶ「方程式」をイメージするとわかりやすいでしょう）。

この問題の場合、チョコレートの個数を○個、おせんべいの個数を□個として式を立てています。

STEP2: 式を簡単にする

次は「式を簡単にする」ステップです。

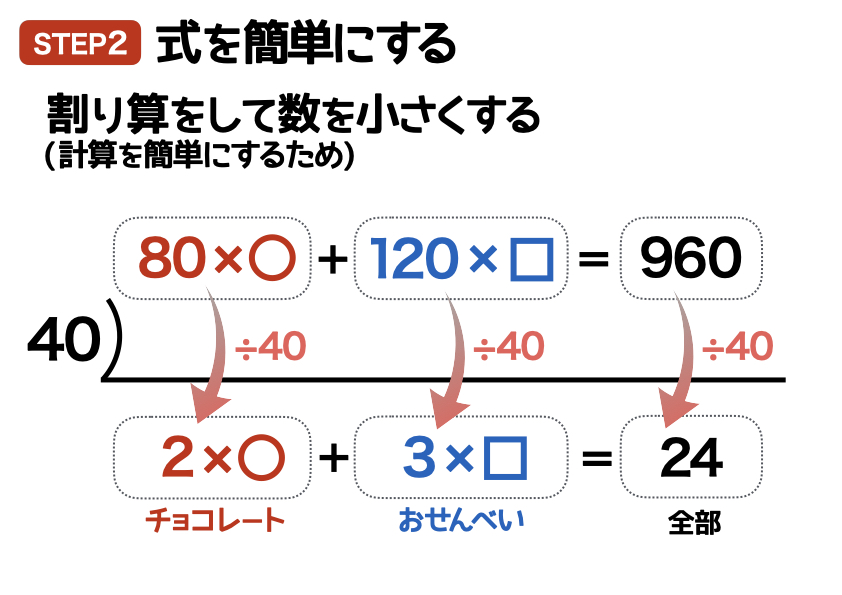
式を簡単にするとは、式にあるすべての項を同じ数で割って、全体的に数字を小さくすること。

この問題の場合は、式全体を40で割っています。

ベストなのは「すべての項の最大公約数」で割ることですが、そこまでこだわる必要はありません。式を簡単にするのは計算を簡単にするためであって、すべての項の最大公約数で割らなくても問題は解けます。

この問題に関しては、登場する数字が80と120と960で、最大公約数が40なので、式全体を40で割ることで最も簡単な式にしています。

STEP3: 表を書く

最後は、でき上がった式をもとに「表を書く」ステップです。

いもづる算は答えがたくさんあるので、全パターンを書き出すつもりで表をまとめましょう（実際には途中まで書くと法則がわかるので、最後まで書く必要はありません）。

チョコレートの個数が0個のとき、1個のとき、2個のとき ―― という感じで、式に登場する値を整理していきます。

こうして途中まで表を書くと、法則性が見えてきます。

法則性が見えてきたら、がんばって表を埋めなくても、チョコレートとおせんべいの個数が「いもづる式」に次々とわかってきますよ。

表を埋めるポイント

表の埋め方について、もうちょっと詳しく見ていきましょう。

ポイントは4つです。

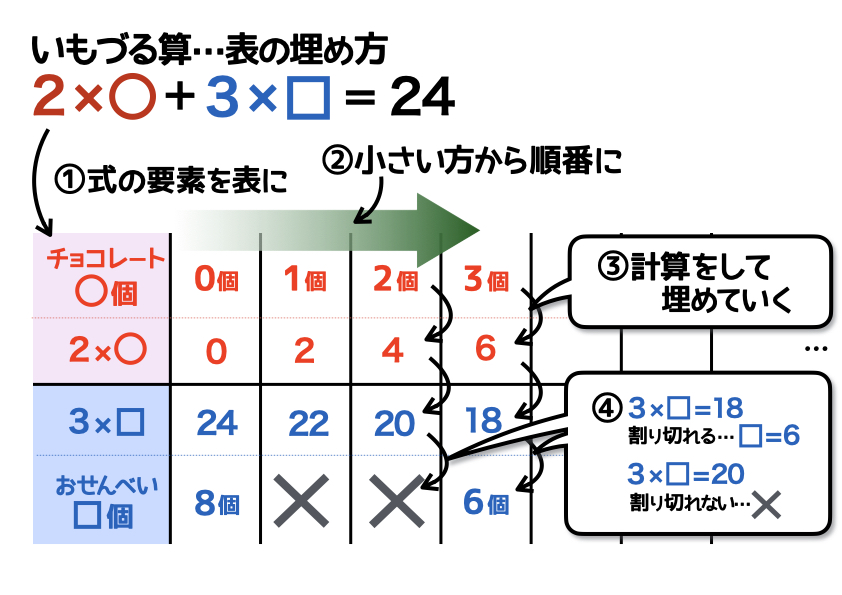
1、表には「式の要素」を書く

表には、式に登場する要素をまとめます。

先ほどの問題の場合は、以下の要素をまとめておくと良いでしょう。

2、小さいほうから順番に埋める

表は小さいほうから順番に埋めていきます。

これは「場合の数」などでも重要な“鉄則”ですが、漏れを防ぐために、必ず小さいほうから順番に表を埋めましょう。

先ほどの問題では、チョコレートの個数を小さいほうから順番に埋めています。

3、計算をして埋めていく

チョコレートの個数○がわかれば、当然「2×○」がわかります。そして「2×○」がわかれば、「3×□」もわかります。

このように計算をして、残りの空欄を埋めていきましょう。

4、割り切れるかに注意する

おせんべいの個数□は、整数でなければいけません（お店では0.5個だけ買うようなことはできませんからね……）。

なので、□が小数や分数になってしまうようなパターン、つまり□を求める式が割り切れない場合はこの問題の条件に合わない、ということになります。

中学入試の出題パターン

中学入試において、いもづる算は主に3つのパターンで出題されています。

［1］シンプルな文章題

中学入試でいもづる算が出題されるほとんどのパターンが、シンプルな文章題です。

この記事で紹介した解法をベースにして練習を重ねていけば、しっかりと得点できますよ。

［2］小問で答えを導かせる問題

少しマイナーですが、小問の指示に従って解いていくと最終的な答えにたどりつくという出題パターンもあります。

この形式のコツは、小問の指示に落ち着いて従うことです。問題そのものが難しく、大問をヒントなしで解こうとするとかなり難しいですが、小問自体は難易度が比較的低めになっています。

ちなみに大問そのものには解法は複数ありますが、その数ある解法のなかで、出題者が受験生に解かせたい解法がそれぞれ小問として出題されています。

まずは落ち着いて、問題の流れに乗りましょう！

［3］ほかの特殊算との融合問題

ほかの特殊算との融合問題が出題されることもあります。

こうした問題は難易度がかなり高いですが、さまざまな文章題の練習をひたすらやることで解けるようになります。

ちなみに特殊算は無数にありますが、私が息子と算数に取り組むなかでメジャーな特殊算をまとめてみたところ、次の24種に分類できました。

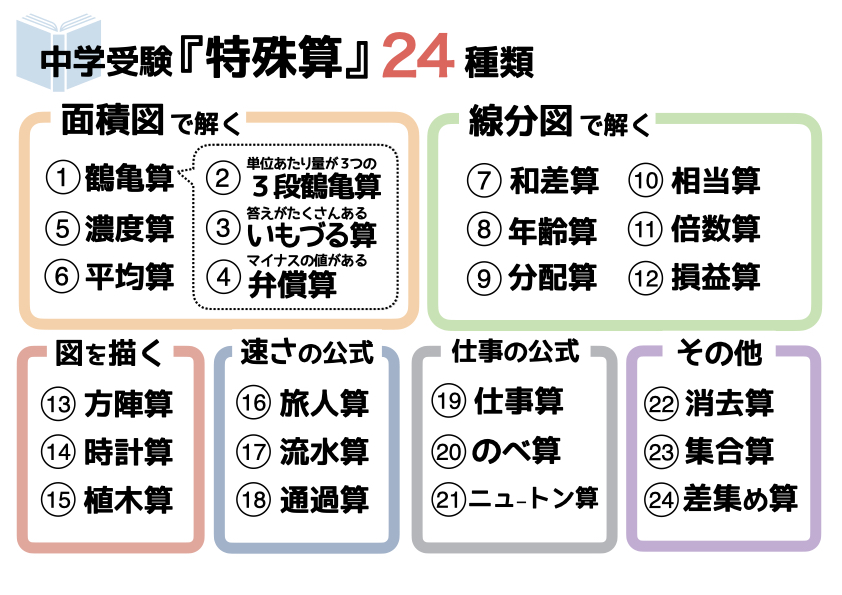
特殊算の全体像は、以下の記事でもまとめています。

中学受験：特殊算は何種類ある？算数の文章題の見分け方

まとめ

特殊算と呼ばれる文章題のうち、やや難易度の高い「いもづる算」について解説しました。

解法そのものを理解していても、いざ本番で文章題を読んだときにどの解法を使えば良いか見分けがつかない……ということは、子供が文章題に苦手意識を感じてしまうひとつの要因です。

まずは基本問題からでOKなので、どの解法を使えば良いかについて、文章題を読んだ時点である程度想像できるようにしておきたいですね。

文章題から何がわかるかによって、解法を判断できるようにしていきましょう！

※記事の内容は執筆時点のものです