植木算第2弾!エレベーターで〇階まで行く・宿題を終わらせるのにかかる時間は?|中学受験算数きほんの「き」!#3
こんにちは!中学受験算数のオンライン個別指導講師 さちです。
「計算くらぶ」にて中学受験算数の計算添削も行っています。
前回の記事では
- 座席の数とひじかけ数の関係
- ろうそくをたてて、その間にいちごをおく
など、ものをならべて考える植木算を紹介しましたが、実はものをならべない植木算もあるんです!
そこで、今回の記事ではものをならべない植木算についてご紹介します!
大切なのは状況を具体的にイメージする想像力です。
算数が苦手な方もクイズ感覚で気軽に取り組んでみてください♪
エレベーターで1階から8階まで行くのにかかる時間は?
それではさっそくスタートです!
<問題1>
あるエレベーターは1階から4階まで行くのに6秒かかります。
このエレベーターが1階から8階まで行くのに何秒かかりますか。

ぜひお子さんと一緒に考えてみてください。
さて、答えは出ましたか?
4階まで行くのに6秒かかるなら、
8階まで行くならその2倍で12秒!
と考える人が多いのですが、残念ながら不正解です。
あれ?なんで?と思ったら、ぜひ図を書いてもう一度考えてみてください。
それでは、解説していきますね。
下にあるのが、問題文の状況を図にしたものです。
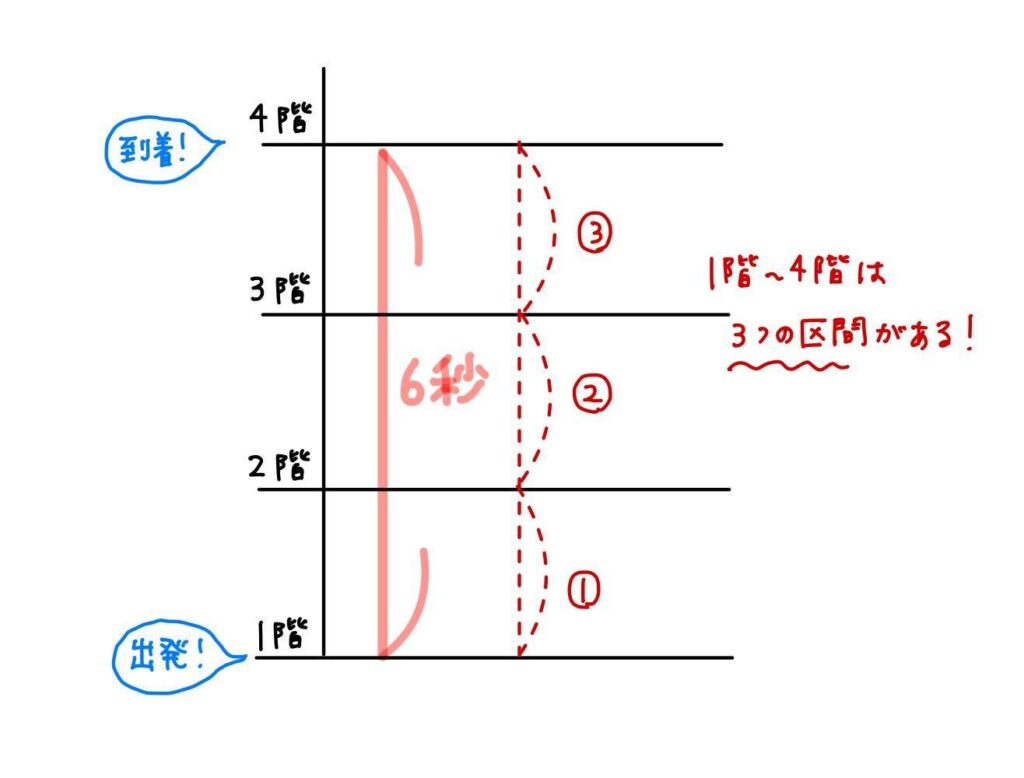
1階から4階まで行くときは
- 1階~2階
- 2階~3階
- 3階~4階
の3つの区間を通ります。
つまり、1つの区間を進むのにかかる時間は
6÷3=2秒ですね。
また、1階から8階までは7つの区間を通ります。
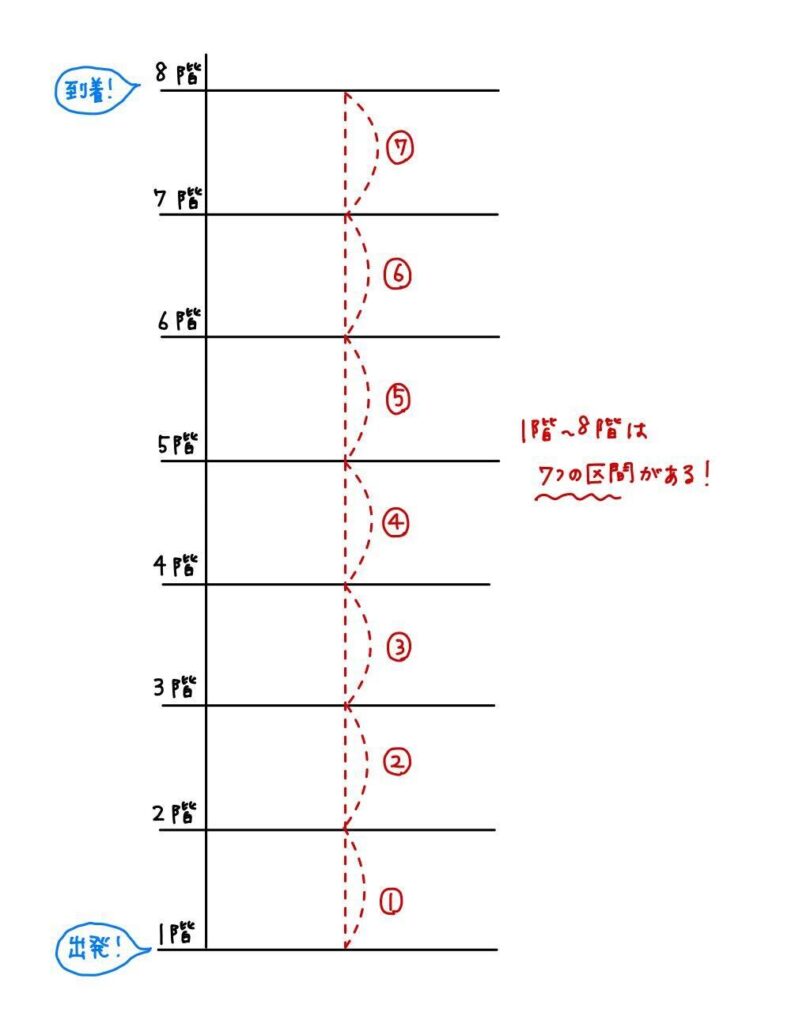
以上より、8階まで行くには
2×7=14秒かかります。
答え. 14秒
- 4階まで行くときは3つの区間を通る
- 8階まで行くときは7つの区間を通る
というように、ある階まで行くのに通る区間の数が、その階数より1つ少ないのがポイントです。
単純に見えてなかなか奥が深い問題でしたね。
算数の宿題にどれくらい時間がかかる?
2つ目の問題です。
こちらもぜひ親子でチャレンジしてみてください!
<問題2>
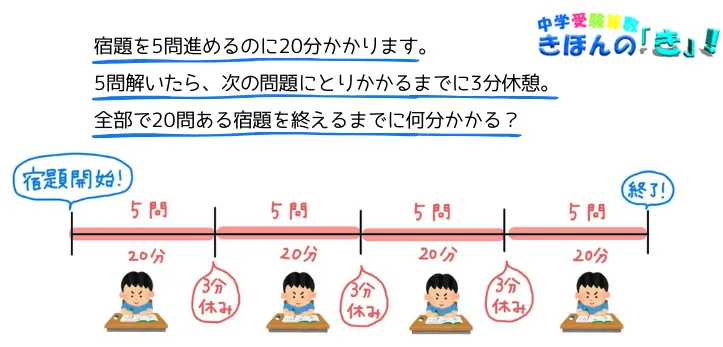
全部で20問ある算数の宿題を5問ずつ進めることにしました。
5問解くのに20分かかります。また、5問解いたら、次の問題にとりかかるまでに3分休みます。
宿題を終えるまでに何分かかりますか。
まずは20問の宿題を5問ずつに分けてみましょう。
20÷5=4
なので、5問×4セットあることがわかりますね。
ここからは図を書いて考えてみましょう。
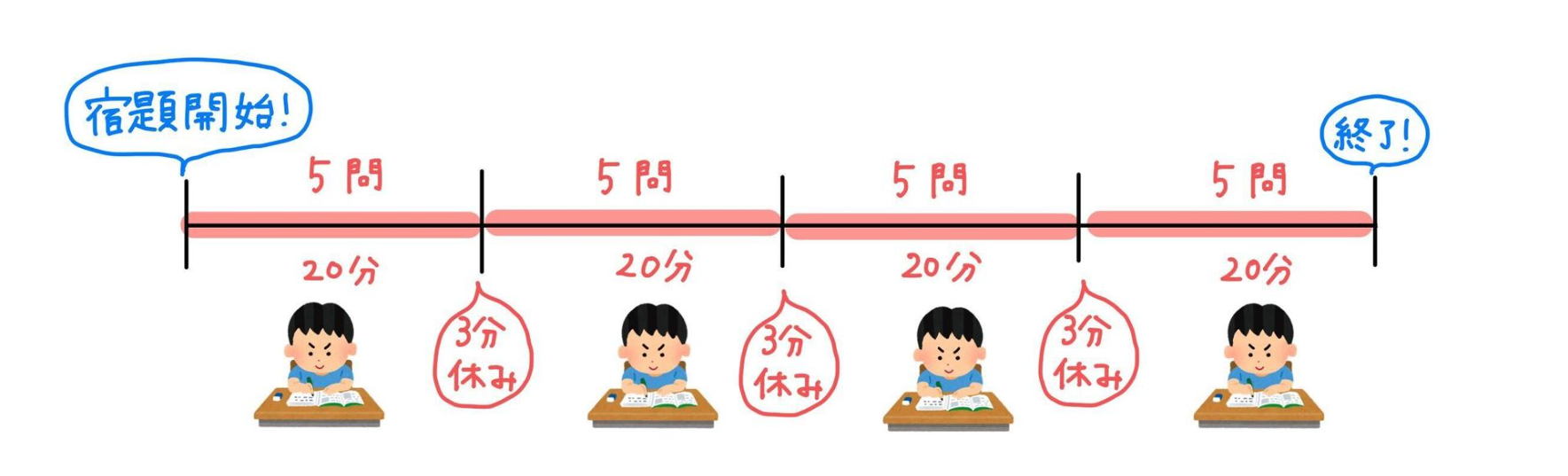
1セットにつき20分かかり、4セット終えるまでに3回休憩するので
20×4+3×3=89
89分かかります。
答え. 89分
(約1時間半かかる宿題…なかなか大変そうですね)
受験算数で定番の「テープをつなげる問題」に挑戦しよう!
最後の問題です。
中学受験算数で定番のテープをつなげる問題に挑戦してみましょう!
<問題3>
1本の長さが12㎝のテープをつなげます。
のりしろを2cmにして10枚つなげると、全体の長さは何cmになりますか。
まずは、テープを2本つなげた時の長さについて考えてみましょう。
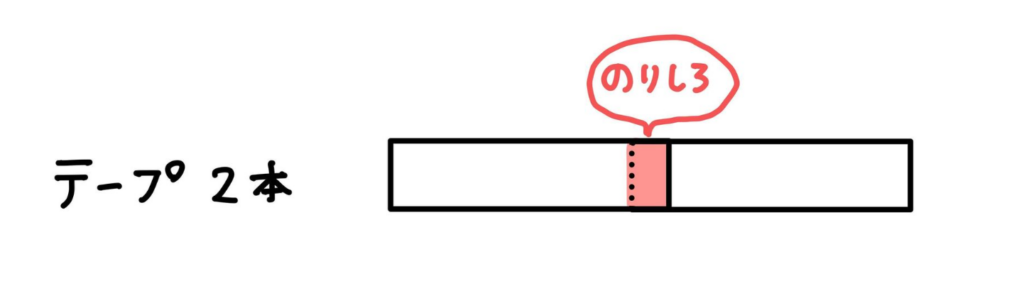
テープを2本つなげると12×2=24cmですが、
のりしろが1か所あるので、そのぶん短くなります。
というわけで、テープを2本つなげた時の長さは
12×2-2×1=24-2=22cm
です。
また、テープを3本つなげた時はのりしろは2か所、4本つなげた時ののりしろは3か所です。
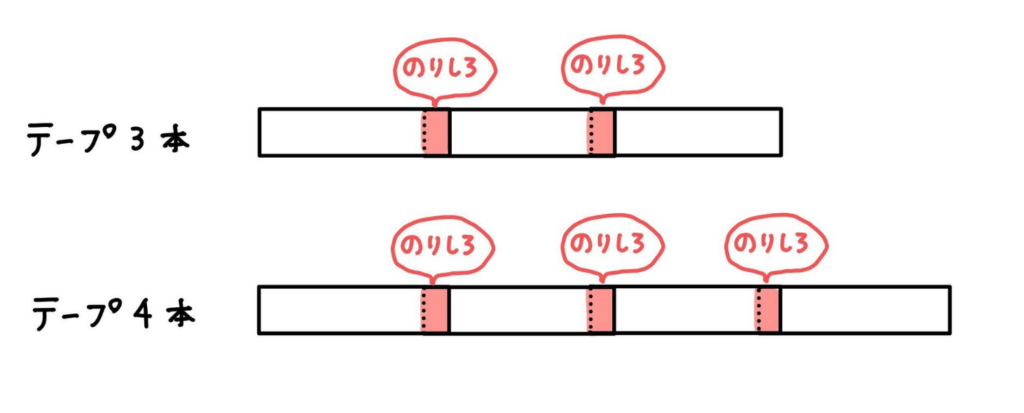
のりしろの数=テープの本数-1
ということが分かりますね。
では、10本つなげた時について考えてみましょう。
このとき、のりしろの数は10-1=9か所です。
10本分のテープの長さからのりしろの長さをひくと…
12×10-2×9=120-18=102
全体の長さは102㎝と分かりました。
答え. 102cm
まとめ
ものをならべない植木算を3問紹介しましたが、いかがだったでしょうか。
- 階数とそこまで行くまでの区間
- 休憩の回数
- のりしろの数
など、問題文に書かれていないことを自分で求める必要があるのが植木算の難しく、おもしろいところです。
- 問題文の状況を具体的にイメージする
- 図を書きながら考える
という算数に必要な力を鍛えられる単元なので、子どもたちがじっくり考えながら取り組めるよう見守ってあげてください。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

