三角形の外角を上手に利用するには？内角との関係を理解して角の大きさを求める

中学受験算数では、三角形の外角を上手に利用して角の大きさを求める問題がよく出ます。そんな外角に関する知識や問題を基本から応用まで解説します。

三角形の内角と外角の関係

多角形において、1つの辺と隣の辺の延長がつくる角が外角です。一方、隣り合う2つの辺がつくる角が内角です。

三角形の内角と外角の関係

三角形の内角と外角の関係では、「三角形の外角は、それと隣り合わない2つの内角の和に等しい」が成り立ちます。下の図では、角ウの隣の外角である角エは、角ウ以外の内角の和に等しいので「角ア＋角イ＝角エ」です。

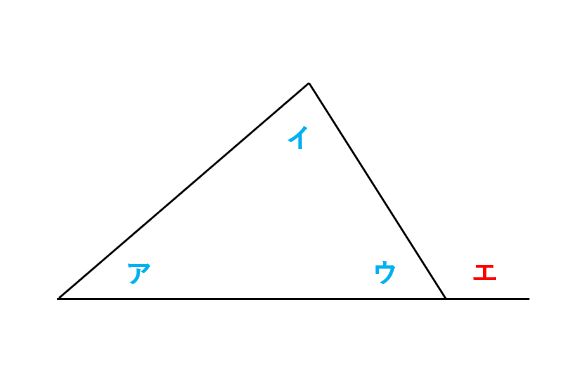
「角エ＝角ア＋角イ」が成り立つ理由を考えてみましょう。三角形の内角の和は180°なので「角ア＋角イ＋角ウ＝180°」となり、「角ア＋角イ＝180°－角ウ」です。また、「角ウ＋角エ＝180°」なので「角エ＝180°－角ウ」です。したがって、「角ア＋角イ＝角エ＝180°－角ウ」が成り立ちます。

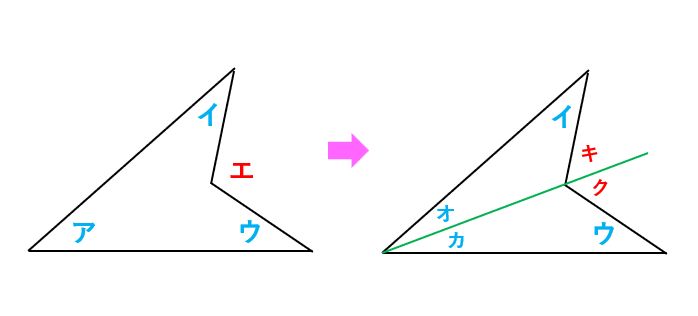
また、図形の角度の大きさを求める問題では、下の左図の「角ア＋角イ＋角ウ＝角エ」を使うこともよくあります。

下の右図のように補助線（緑の線）を引くと、「角イ＋角オ＝角キ」「角ウ＋角カ＝角ク」より「角イ＋角ウ＋角オ＋角カ＝角キ＋角ク」が成り立ち、「角オ＋角カ＝角ア」「角キ＋角ク＝角エ」なので「角ア＋角イ＋角ウ＝角エ」が成り立つことを説明できます。

三角形の外角の和は360°

三角形の外角の和は360°です。これが正しいことを下の図を使って説明してみましょう。

「外角の和＝角エ＋角オ＋角カ」です。また、「角ア＋角エ＝角イ＋角オ＝角ウ＋角カ＝180°」より「内角の和＋外角の和＝角ア＋角イ＋角ウ＋角エ＋角オ＋角カ＝180°×3＝540°」です。さらに、三角形では「内角の和＝角ア＋角イ＋角ウ＝180°」より「内角の和＋外角の和＝180°＋角エ＋角オ＋角カ＝540°」となり、「外角の和＝角エ＋角オ＋角カ＝540°－180°＝360°」が正しいことがわかりました。

外角の和が360°になるのは三角形だけではありません。すべての多角形の外角の和は360°です。これが正しいことも、三角形の場合と同じように説明できます。

三角形の内角の和が180度になるのはなぜ？ 角度の基本を多角形にも応用しよう

ほとんどの小学生は「三角形の内角の和は180度」を知っています。しかし、このことが成り立つ理由をきちんと説明できる小学生...

三角形の外角を利用して解く問題

角の大きさを求める問題は、三角形の外角を上手に利用することで解けることがあります。そんな問題の中から、代表的な問題の解き方を解説します。

基本問題の解き方

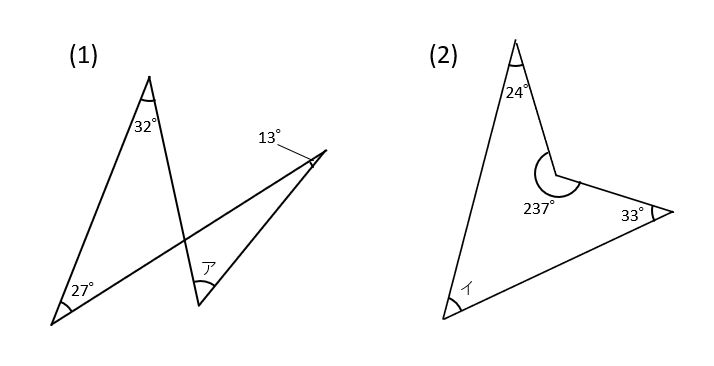
(1)では、下の図のように、左側の三角形の内角の和（32°＋27°）から外角（59°）を求めます。この外角は右側の三角形の外角にもなっているので、内角の和（角ア＋13°）も59°とわかります。したがって、角ア＝59°－13°＝46°が答えです。

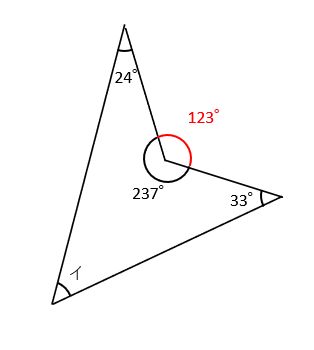
(2)では、下の図のように360°－237°＝123°を求めると、角イ＋24°＋33°＝123°です。したがって、角イ＝123°－24°－33°＝66°が答えです。

応用問題の解き方

【問題2】では、左の三角形から順に、内角の和を使って外角の大きさを求めていきます。

まず、下の図で三角形ABCはAB＝BCの二等辺三角形なので角BCA＝角BAC＝アで、角CBD＝角BAC＋角BCA＝ア×2です。また、三角形CBDはBC＝CDの二等辺三角形なので、角CBD＝角CDB＝ア×2です。

次に、下の図で三角形ACDに注目すると、角DAC＝ア、角ADC＝ア×2で、角DCE＝角DAC＋角ADC＝ア×3です。また、三角形DCEはCD＝DEの二等辺三角形なので、角DEC＝角DCE＝ア×3です。

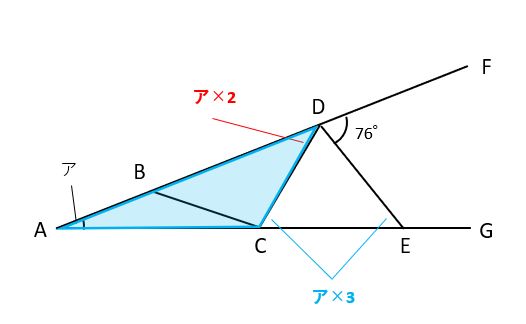
最後に、下の図で三角形ADEに注目すると、角DAE＝ア、角DEA＝ア×3で、角EDF＝角DAE＋角AED＝ア×4です。ア×4＝76°よりア＝76°÷4＝19°が答えです。

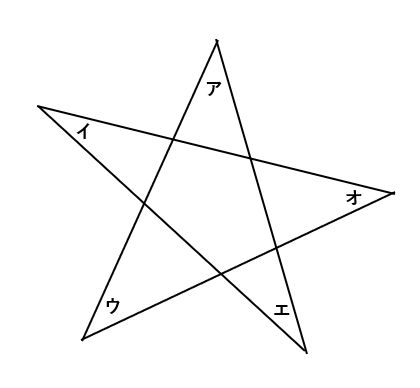
【問題3】は、星形の図形の角の和を求める有名な問題です。答えが180°になることを知っている受験生もいるでしょう。しかし、答えを丸暗記して終わりにするのではなく、「どうして180°になるのか？」を考えることが大切です。

まず、下の図で赤い図形に注目すると、角の大きさがア＋ウ＋エになる角がわかります。

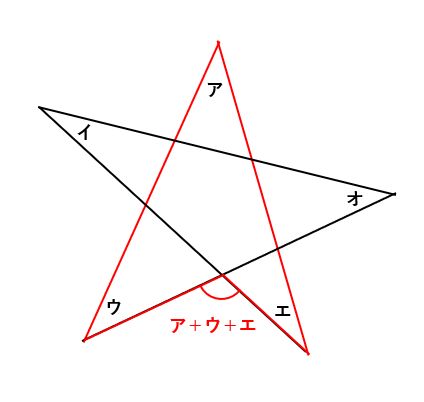
次に、下の図で青い図形に注目すると、角の大きさがイ＋オになる角がわかります。

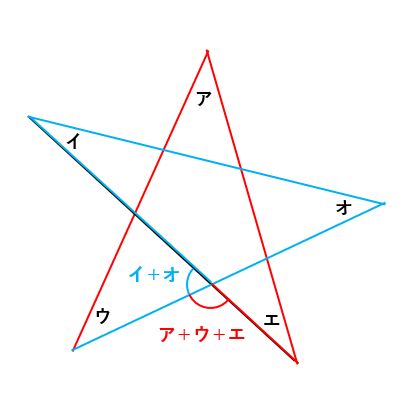
以上より、ア＋イ＋ウ＋エ＋オ＝180°が答えです。星形の図形に限らず、複雑な図形の角の大きさを求める場合、図形を分割して内角と外角の関係を上手に使いましょう。

角度の求め方をわかりやすく解説！ 平行線や多角形の角の特徴や公式を理解する

中学受験算数では、角度を求める問題がよく出ます。平行線と角度の性質に注目したり、多角形の内角や外角の和の公式を利用し...

三角形の外角の知識は中学数学でも使う

三角形の外角の知識は中学数学でも使うので、中学受験算数の勉強で習得しておくと、中学進学後に有利になります。それぞれの問題の解き方を覚えるだけでなく、「どうしてそうなるのか？」を理解することで、算数の力が伸びるはずです。

※記事の内容は執筆時点のものです