
「速度の公式」をマスターする勉強法
「速度」は「比例」の感覚に加えて、時間の「単位換算」を同時に求められ、苦手と感じる子供が多い分野です。逆の言い方をすれば「比例」と「時間の単位換算」ができるようになれば、ある程度「速度」の問題は解けるようになります。
Contents
「比例」を徹底的に復習しよう
「速度」をマスターしたいと思ったら、まずは「比例」の復習をしっかりするのが大切です。
「速度」問題の用語の意味を理解しよう
「速度」の問題を解く際には用語の理解が欠かせません。例えば「時速30km」というのは、「1時間あたり30km進む速さ」ということです。試しに次の問題を考えましょう。
【問題】
120kmの距離を6時間で走る速さは時速何kmですか。
もちろん暗算で時速20kmと求めることができそうですが、表にすると下のようになります。
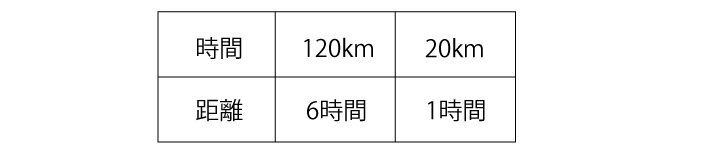
「比例」のときに学んだ表と酷似していますね。
「速度」は「比例」と同じ考え方をする単元なのです。
「比例」「割合」をまず復習しよう
「速度」が苦手な人はまず「比例」の単元を復習するとよいでしょう。
後述しますが、速度の学習には、時間の単位換算も必要になるので、「比例」よりも複雑で難しい単元です。
とくに「比例」で表をつくる感覚が身についていないと、速度の学習がただの公式の暗記になってしまう可能性があります。
「単位換算」をマスターしよう
「速度」では単位換算が求められます。この換算がうまくできないと「速度」の問題を解くのは難しく、苦手意識が強くなってしまうかもしれません。では、「速度」で必要となる単位換算をみていきましょう。
「時間」「長さ」の単位換算を覚える
●覚えるべき「時間」の単位換算
1時間=60分、1分=60秒、(1時間=60分=3600秒)
●覚えるべき「長さ」の単位換算
1km=1000m、1m=100cm
「速度」の単元で覚えるべき単位換算はこの程度。膨大な量の単位換算を覚えるわけではないとわかれば、少し安心できるかもしれません。「大したことないじゃん!」と思えればこっちのものです。
また、「単位の意味」を知っていると少しは楽に覚えられるかもしれません。
たとえば「k(キロ)」という単位。
k(キロ)は「×1000」を意味します。つまり1kmとは1×1000m、すなわち1000mということです。
これは長さの単位だけにとどまりません。1kg=1000g、1kL=1000Lですよね。「×1000」という「単位の意味」が共通の概念であるとわかると理解が深まり、1kg や1kLの換算を 1つ1つ丸暗記していくより効率よく覚えることができそうです。
「速度」の単位を換算する
ここまで理解できれば、「速度」の単位換算もできるはずです。次の問題を考えてみましょう。
【問題】
□にあてはまる数を求めなさい。
(1)秒速12m=分速□m
(2)秒速15m=分速□m=時速□km
(3)時速36km=秒速□m
(1)の「秒速12m」は1秒で12m進むということです。
分速□mとは1分で進む距離、すなわち60秒で進む距離です。
1秒で進む距離が12mなので、60秒では12×60=720m進みますね。
答えは「分速720m」となります。
(2)も同様に進められればOKです。
分速は15×60=900となるので、分速900m。
時速は900×60=54000mとなります。kmで解答するように指示されているので、54000m=54kmと変換して、答えは「時速54km」とわかります。
(3)は(1)の逆ですね。時速36km=時速36000mです。
分速にするために60でわって、36000÷60=600、つまり分速600m
秒速にするために60でわって、600÷60=10、答えは「秒速10m」となります。
「速度」は難しくない!
以上の内容がわかっていれば、速度は難しくありません!
つまずいてしまったら、「比例」「単位換算」に戻って考えるようにすれば大丈夫です。
速度の公式「は・じ・き」公式から脱却しよう
「速さ・時間・距離」の関係を公式にした「は・じ・き」公式が有名ですが、公式を使って求めるのはおすすめできません。丸暗記してしまうと理解が深まらず、応用に強くなれません。
比例の感覚を応用して、公式なしで速度の問題を解けるように訓練すべきです。
【問題】
(1)時速3.6kmで歩く人がいます。3240mの道のりを歩くには何分かるでしょうか。
(2)秒速15mで走る電車があります。135km進むには何時間何分かかるでしょうか。
(3)6.75kmの道のりを1時間15分で歩きました。速さは秒速何mでしょうか。
(1)時速3.6kmは60分で3600mと同じことなので、1分あたりだと3600÷60=60となる。すなわち分速60mになります。表にすると次のようになります。
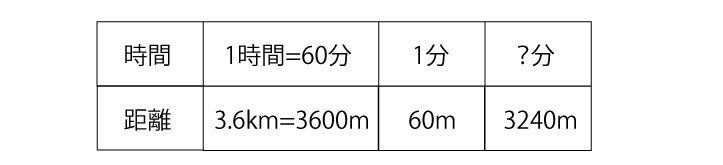
こうなれば3240÷60=54分で、答えは「54分」とすぐわかります。
まさに「速さ」は比例の感覚を使って解く割合の計算そのものです。
(2)求めるのは「135km」を「何時間何分」で進むかです。
求めるは「km」と「時間」なので、秒速15mを時速○○kmに変換します。「1時間=3600秒」なので、1時間だと「15m×3600秒=54000m=54km」進む、すなわち「時速54km」となります。こちらも表にしてみましょう。

求めるのは「135÷54=2 \(\frac{1}{2}\)時間」となるので、答えは「2時間30分」となります。
(3)求めるのは「秒速」「m」なので、「1時間15分=75分=4500秒」、「6.75km=6750m」と単位を揃えます。この問いを表にすると以下のようになりますね。

秒速とは1秒あたりに進む距離なので、「6750÷4500=1.5」となります。したがって、答えは「秒速1.5m」です。
「だいたい感覚」で間違いに気づこう
採点をしているとよくある誤答で、「人の歩く速さが時速60km」「隣町までの距離が3000km」といった解答です。どこが変かわかりますか?
100mを10秒で走ればオリンピック選手も夢ではありませんが、この場合でも時速36kmです。ということは人の歩く速さが時速60kmというのは明らかにおかしいですね。
隣町までの距離3000kmというのも、日本の全長が約3800kmということを考えると明らかにおかしい。
つまりこれらの解答は「常識的にあり得ない」解答なのです。(計算ミスって恐ろしい……)人の歩く速さ、隣町までの距離、といった設定からみたときに「あれ? これは速すぎるかな? 遠すぎるかな?」と気づけるかどうかは、歩く速さや実際の距離について「だいたいの感覚」を持っているかにかかってくるのです。
この感覚があると少なくとも「あり得ない解答」が回避できるはず。
「だいだいの感覚」を身につける方法は、日常生活にある「速さ」について、普段から考える習慣をつけておくことです。
たとえば、車に乗っていたら「今、時速何kmだろう?」、駅まで徒歩5分というけど「徒歩の速さは分速何m?」というように、身近なところで常識的な速さを考えてみましょう。常識の範囲を知っておけば「だいだいの感覚」が身につき、計算間違いにも気付けそうですね。
「速度」攻略のカギは「比例」と「単位換算」
「速度が苦手」という生徒は多いですが、原因は人それぞれです。「比例」がわかっていないのか、「単位換算」ができないのか。原因を明らかにして丁寧に取り組めば必ずできるようになる単元です。基礎に戻って、「速度」を得意分野にしてくださいね。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

