
【台形の面積公式】暗記よりも理解が大事! 応用が利く図形問題の考え方
台形って少し特殊な図形ですよね。面積公式も{(上底)+(下底)}×(高さ)÷2と少し複雑です。台形がちょっと苦手と思う人は意外と多いようです。でも本質が理解できれば、応用がぐっと広がるところでもあるのです。
Contents [hide]
三角形は台形!?
まずは図形の考え方から! 公式の本質を理解するときにカギとなるのは三角形と台形の2つの図形の深い関連です。
台形の面積公式に注目。「上底」をどんどん小さくしていくと……!?
「三角形は台形です」と言われたらどう思いますか?「ちがう図形です」と思いますよね。台形は四角形です。テストで三角形のことを「台形」と答えたら不正解になってしまうでしょう。
では、三角形と台形にどのような深い関連があるのか。まず実験してみましょう。たとえば下の図は台形ですよね。でも図のように上底を短くしてみると……。どんどん三角形に近づいていくのです!
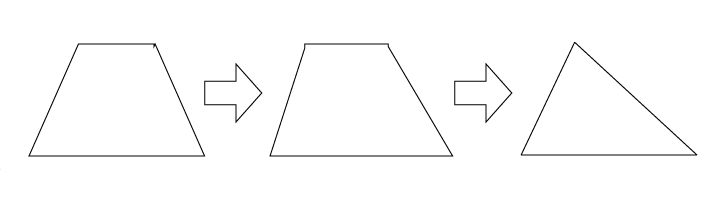
つまり三角形は「上底の長さが0の台形」と言えるのです。
台形の面積公式
{(上底)+(下底)}×(高さ)÷2 でも、
(上底)=0 とすると、
(下底)×(高さ)÷2 となり、
たしかに三角形の面積公式と同じになりますね。
長方形、正方形、平行四辺形もすべて台形と考えられる!
同じように考えていくと、(上底)と(下底)の長さが等しい台形は平行四辺形となりますし、平行四辺形のなかで、4つの角が90度になるものが長方形、さらにすべての辺の長さが等しくなったものが正方形と言えますね。この関係をまとめたものが下の図になります。
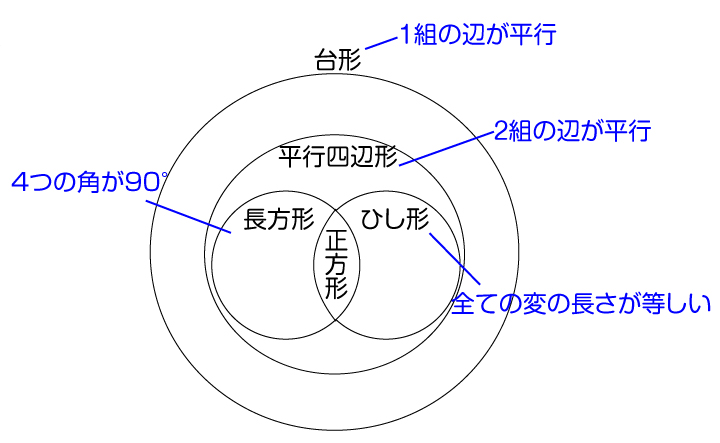
(上底)と(下底)が平行である図形はすべて台形と考えることができ、台形の面積公式{(上底)+(下底)}×(高さ)÷2ですべての面積を求めることができるのです。
面積比の問題がこんなに簡単に!
様々な図形が「台形」であることを確認しました。実はこれがいろいろな問題に応用できるのです!
平行線と面積比の問題
たとえば下の問題、どのように考えるでしょうか。
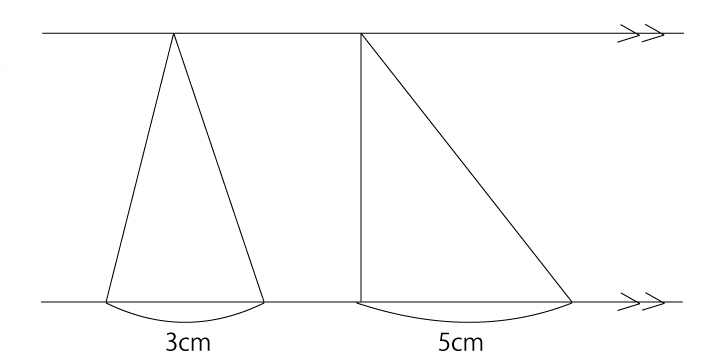
高さの等しい三角形の面積比は『底辺の長さの比』
なので、面積比は3:5ですね。
この考え方を台形に応用してみましょう。
台形の面積公式
{(上底)+(下底)}×(高さ)÷2 から、
高さの等しい台形の面積比は『(上底)+(下底)の大きさの比』
になることがわかります。
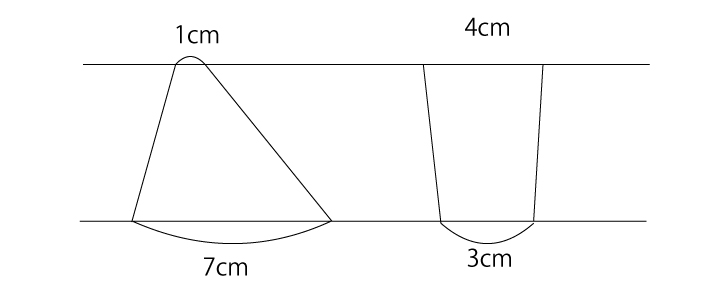
上の2つの図形の面積比は、(1+7):(4+3)=8:7になることがわかりますね。
高さが等しい三角形、長方形、台形の面積比
ここで「三角形は台形である」を思い出してみましょう。三角形や長方形、正方形に台形の面積公式が適用できたことを考えると、同じように(上底)+(下底)の大きさの比だけで、面積比を出すことができてしまうのです!
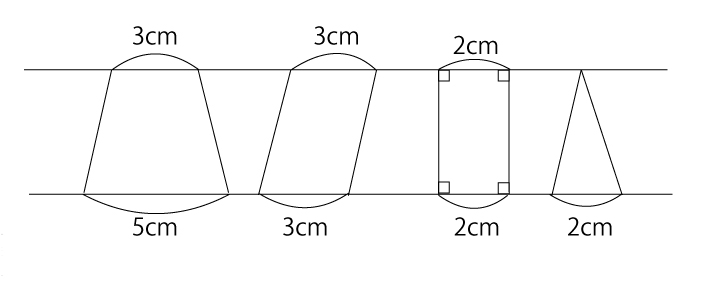
上の4つの図形は左から、台形、平行四辺形、長方形、三角形と名称は
異なりますが、面積比は、
(3+5):(3+3):(2+2):2=8:6:4:2=4:3:2:1
のように簡単に計算できるのです。
実際の入試問題にも多数出題
ここまでの内容が理解できると、難関中学で出題されるような難問にもどんどん応用できるようになります。
点が動く問題
<問題>
下の図のような台形ABCDがあります。動点PはAからDに向かって、QはCからBに向かって、それぞれ毎秒1cm、毎秒2cmで同時に出発します。四角形ABQPの面積が台形ABCDの半分になるのは、何秒後でしょうか。
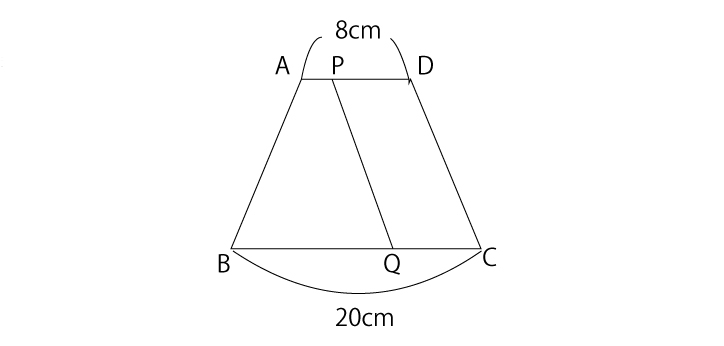
四角形ABQPは最初は三角形ですし、その後は台形になりそうですが、平行四辺形になるときもありそうです。でも、みなさんにはもう関係ありませんね。大切なのは(上底)+(下底)の大きさだけです。
まず全体の台形ABCDは上底=8cm、下底=20cmなので、8+20=28cmです。つまり、四角形ABQPの上底+下底=14cmになるときを求めればよいのです。
最初は上底=0cm、下底=20cmなので、上底+下底=20cmですね。
1秒ごとにPが1cm上底を長くして、Qが下底を2cm短くします。
つまり1秒で上底+下底は1cmずつ小さくなります。
以上のように考えると、最初に上底+下底=20cmだったのが、14cmになるのは「6cm短くなったとき」すなわち「6秒後」と求めることができますね。
台形の面積公式は「本質」の理解がカギ! 得意になれば応用は無限大
たくさん習う面積公式ですが、図形の関係性を深く理解していると応用が利く場面がたくさんあります。特に台形のように一見面倒に見えるものこそ、ほかの図形に応用できるヒントが隠されているものです。台形の面積公式を理解して、どんどん応用に使ってみてください。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

