電熱線の抵抗と電流や発熱量の関係を整理しよう

電熱線は長さ、太さ、抵抗、電流、電圧、発熱量といった要素間の関係を決して覚えようとせず、常識として理解するよう努めてください。

電圧が増えれば電流も増えるし、抵抗が大きくなれば電流は減って当たり前だという感覚で、オームの法則（電流＝電圧 / 抵抗）を理解するのと同じです。

常識という土台の上に「電熱線の発熱量は、電流×電流×抵抗に比例する」という知識を上乗せすれば、電熱線は万全となるでしょう。

電熱線の長さと抵抗の関係～豆電球を直列につないだ場合と同じ

電気回路とは、導線につながれた抵抗に対して、電池が電圧を加えるものです。豆電球も電熱線も、抵抗であることに変わりはありません。どちらも無理やり電流が流れて熱が発生し、多かれ少なかれ光ります。

異なる点は、発生する熱と光のうち主に光を利用する道具が豆電球であるのに対して、電熱線は熱を利用する道具だということです。

抵抗である電熱線が長くなることは、豆電球（抵抗）を直列につなげるのと同じ状態と言えます。つまり長い電熱線ほど抵抗は大きく、同じ電圧であれば電流は小さくなります。

電熱線の長さと抵抗～電熱線の長さが1の場合

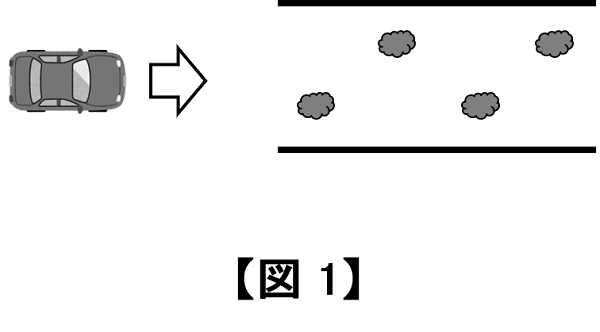
【図1】は、車を電気の粒、車のエンジンを電圧、車の流れを電流、障害を抵抗、障害のある道を電熱線と置き換えながら眺めてください。

これまで順調に走っていた車が、障害のある道に進入します。【図 1】の状態を、「電流（車の流れ）＝電圧（エンジン：1）÷抵抗（障害：1 ）＝ 1」とみなして比較してみましょう。

電熱線の長さと抵抗～電熱線が長くなった場合

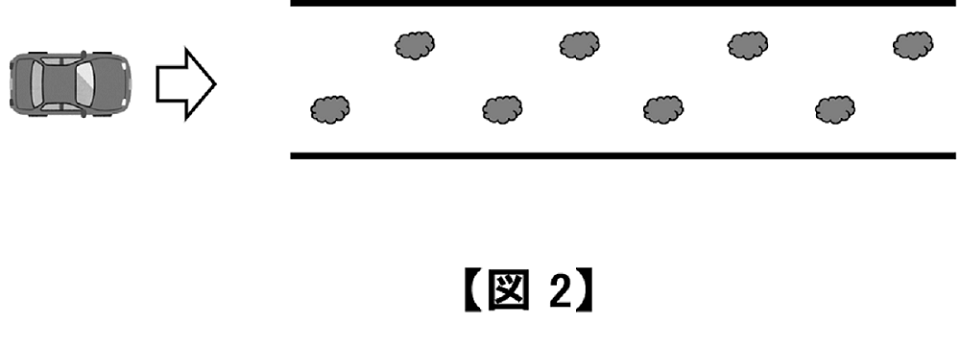
障害のある道が長くなれば、車は通りにくくなり流れも悪くなります。【図 2】では、「電流（車の流れ）＝電圧（エンジン：1）÷抵抗（障害：2）＝\(\frac{1}{2}\)」となり、電流は小さくなります。

豆電球の直列つなぎも、【図 2】と全く同じ絵を使って説明することができます。つまり「電熱線が長くなる」ことと「豆電球を直列につなぐ」ことは物理的に同じで、抵抗が大きくなり電流は小さくなります。

以上が「電熱線の長さ」と「電熱線の抵抗」と「電流の大きさ」との関係です。注意していただきたいのですが、まだ発熱量に触れていません。【図 1】と【図 2】で、どちらの発熱量が多いのかは後述します。

電熱線の太さと抵抗の関係～豆電球を並列につないだ場合と同じ

子供にとって「太い電熱線ほど電流は流れやすい」と直感的に考えることは容易だと思いますが、それを「並列つなぎの豆電球」と結びつけるのは至難の技と言えるかもしれません。

いったん基本に戻って、「電熱線の太さ」と「並列つなぎの豆電球」と「電流」との関係を整理してみましょう。

電熱線の太さと抵抗～電熱線が太くなった場合

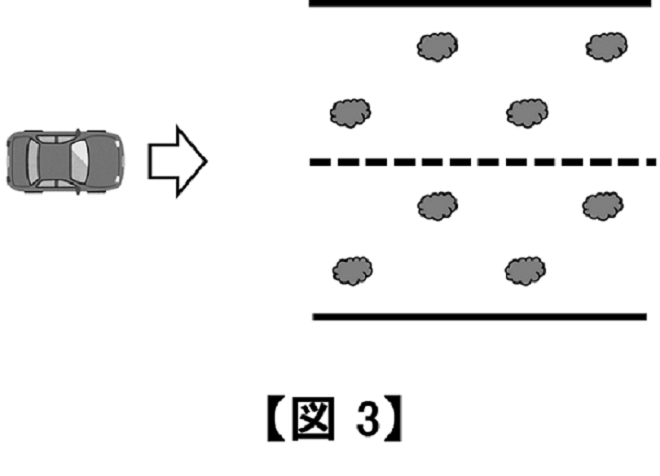
【図3】は【図 1】と比べて、車は通りやすいのでしょうか、通りにくいのでしょうか。初めは「通りやすい」と答えていた子供も、「上側の道を通っても、下側の道を通っても、車にとって通りやすさは変わらないのでは？」と投げかければ徐々に意見が割れてきます。

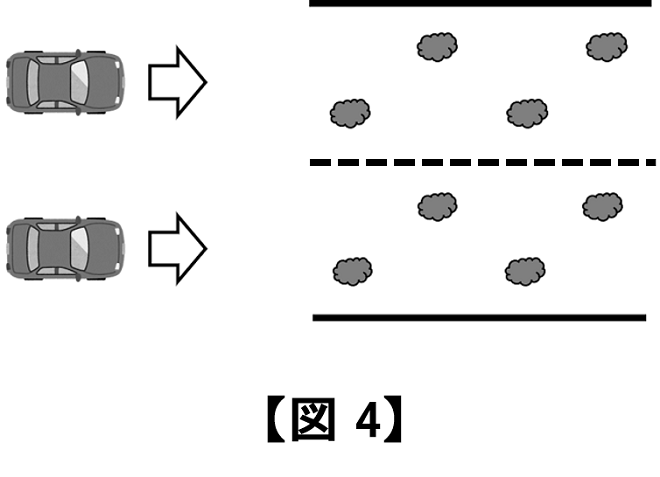
答えは、「1台の車にとって通りやすさは変わらないが、全体では同じ時間内に2台の車が通り抜けられる。」というものです。

電熱線を太くするのは、車の通り道を増やすようなものです。豆電球を並列につなぐと電流の通り道が増えて、それぞれの豆電球に同じ電流が流れるのと同じです。

以上をまとめると、「電熱線の太さが2倍になると、電流も2倍になる」または「電熱線の太さが2倍になると、抵抗は\(\frac{1}{2}\)になる」と言えます。つまり「電熱線が太くなる」ことと「豆電球を並列につなぐ」ことは物理的に同じで、全体の抵抗は減り電流が増えます。

「電熱線の長さや太さ」「抵抗」と「豆電球の直列・並列つなぎ」との類似性までは、常識的な感覚で理解したほうが間違いは減るはずです。

電熱線の電流と発熱量の関係～電流×電流×抵抗に比例する

電熱線に流れる電流が大きくなれば発熱量も増えることは、容易に想像することができます。ところが「電流」と「電熱線の発熱量」との関係を深く問われると、よほど注意深く考えなければ間違えてしまいます。

例えば【図 1】で車のエンジンパワーを2倍にすれば、同じ時間内に2台の車が通り抜けられるはずです。【図 4】も2台の車が通り抜けていますから、通り抜ける車の数は同じということになります。

電圧を2倍にしても抵抗を「2分の1」にしても、ともに電流は2倍となりますが、発熱量は異なります。このレベルでミスなく問題に向き合うためには、発熱量が「電流×電流×抵抗」に比例するという知識を備えておくと良いでしょう。

電熱線の電流と発熱量～抵抗は同じ、電圧が2倍の場合

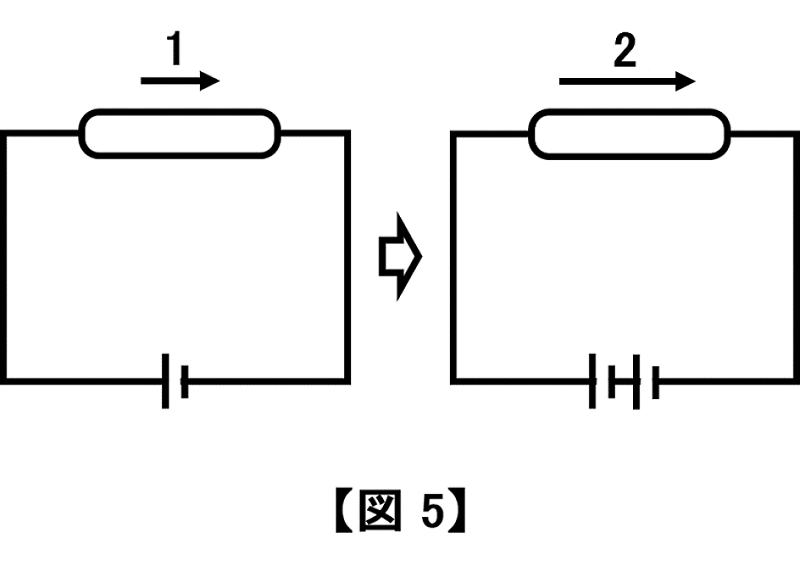
【図 5】は、抵抗を変えずに電圧を2倍にすることによって、電流を2倍にしています。このとき左に対する電熱線（右）の発熱量は、「電流×電流×抵抗」＝「2×2×1」＝4倍となります。

電熱線の電流と発熱量～電圧は同じ、抵抗が\(\frac{1}{2}\)の場合

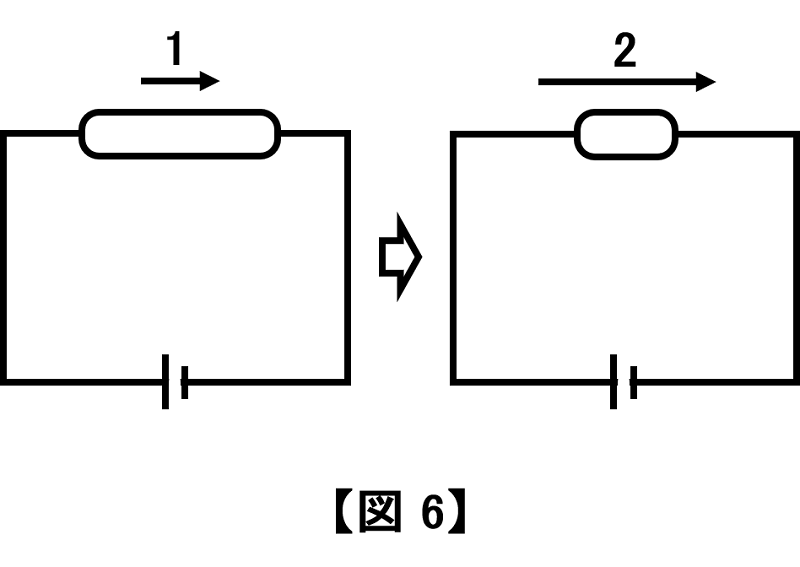
【図 6】は、電圧を変えずに抵抗を\(\frac{1}{2}\)にすることによって、電流を2倍にしています。このとき左に対する電熱線（右）の発熱量は、「電流×電流×抵抗」＝「2×2×\(\frac{1}{2}\)」＝2倍となります。

【図 5】【図 6】ともに電流は2倍となっていますが、電熱線の発熱量は増え方が異なる点に注意してください。

なお【図 1】（電流×電流×抵抗＝1×1×1＝1）と【図 2】（電流×電流×抵抗＝「\(\frac{1}{2}\)」×「\(\frac{1}{2}\)」×2＝\(\frac{1}{2}\)）を比較すると、電流の大きい【図 1】のほうが発熱量は多いです。

【図 1】と【図 4】（電流×電流×抵抗＝2×2×「\(\frac{1}{2}\)」＝2）を比較すると、電流の大きい【図 4】のほうが発熱量は多いです。

電熱線の発熱量が「大きい」のか「小さい」のかを問われている場合は常識で考えればいいのですが、具体的な電熱線の発熱量を問われたら「電流×電流×抵抗」に比例することを必ず思い出してください。

まとめ

◎ 「電熱線が長くなる」ことと「豆電球を直列につなぐ」ことは同じで、電流は小さくなり電熱線の発熱量も小さくなります。

◎ 「電熱線が太くなる」ことと「豆電球を並列につなぐ」ことは同じで、電流は大きくなり電熱線の発熱量も大きくなります。

◎ 電熱線の発熱量を具体的に求める必要がある場合は、電熱線の発熱量が「電流×電流×抵抗」に比例するという知識を用いましょう。

※記事の内容は執筆時点のものです