線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る

線対称と点対称は、小学校入試にも出題されるほど算数ではメジャーな分野ですね。小学6年生が受験する中学校入試ではどのように扱われるのでしょうか？

中学受験は線対称と点対称を作図できるだけでは攻略できません。多くの入試問題では、線対称や点対称の性質を条件として使わないと解けないような出題のされ方をします。

この手の問題は、そのポイントに気づけるか気づけないかで差が発生することが多く、合否を分ける重要な問題となる可能性もあるので、しっかりおさえておきたいところですね。

まずは線対称と点対称の性質をおさえるところから始める

それではどのように対策をすればよいでしょうか？ 冒頭でご紹介した通り、線対称や点対称の図形を作図できだけでは不十分です。入試問題に対応できる力をつけるためには、線対称と点対称の「性質」をおさえる必要があります。ただし恐れることはありません。実は性質自体は難しいものではなく、とてもシンプルでわかりやすいものです。

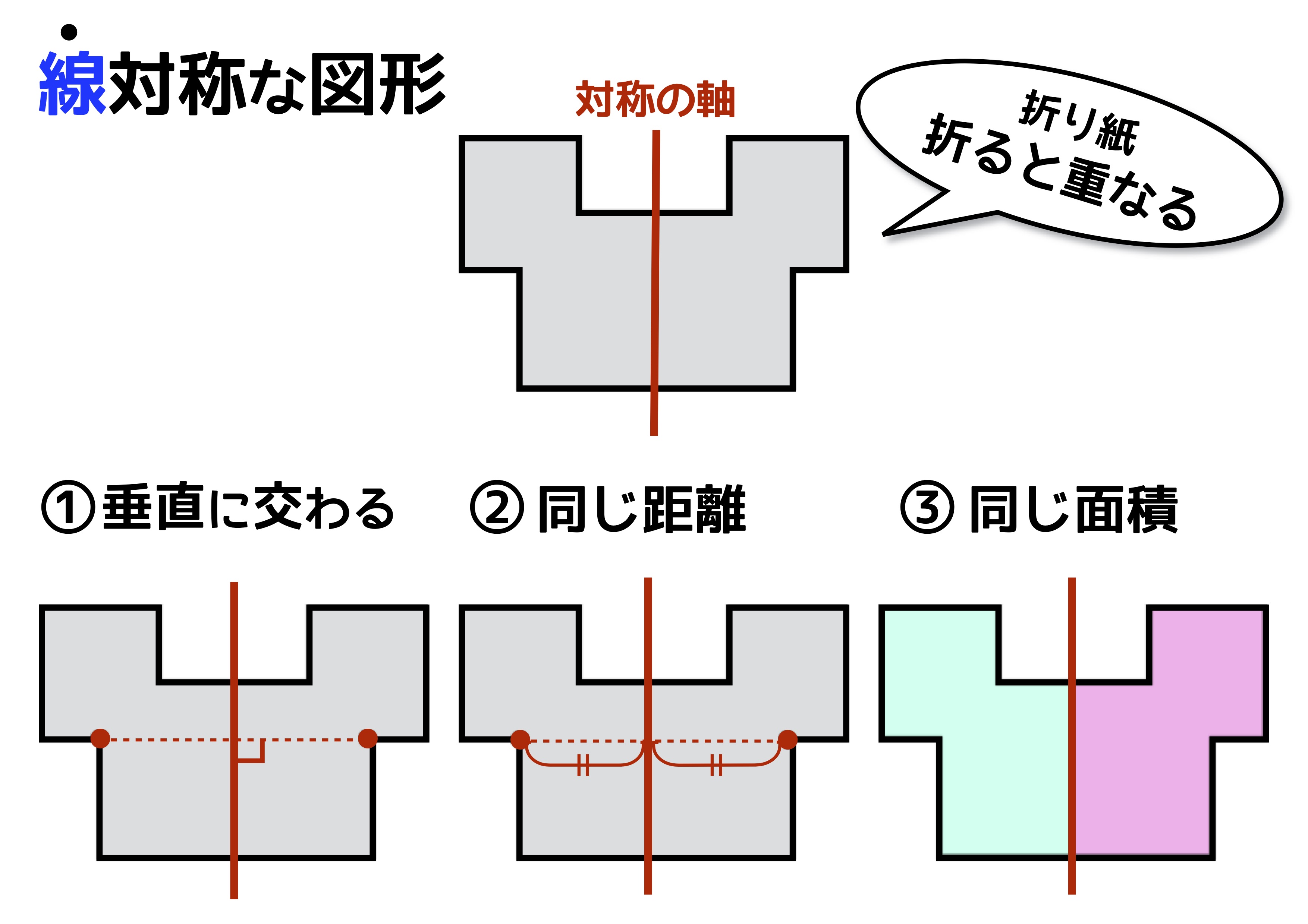
「線対称」のおさえるべき性質

まずは、線対称から。線対称は「折り紙のように折るとぴったり重なる図形」ですね。ここでいう折り目のことを「対称の軸」といいます。

さて本題の性質です。3つの性質をおさえましょう。

ひとつ目は、対応する点を結ぶと対称の軸と垂直に交わるという性質。ふたつ目は、交わる点から対応する点までは同じ長さであるという性質。みっつ目は、対称の軸の両側にある対応する図形の面積は等しいという性質です。

身構えるほど難しくありませんね！

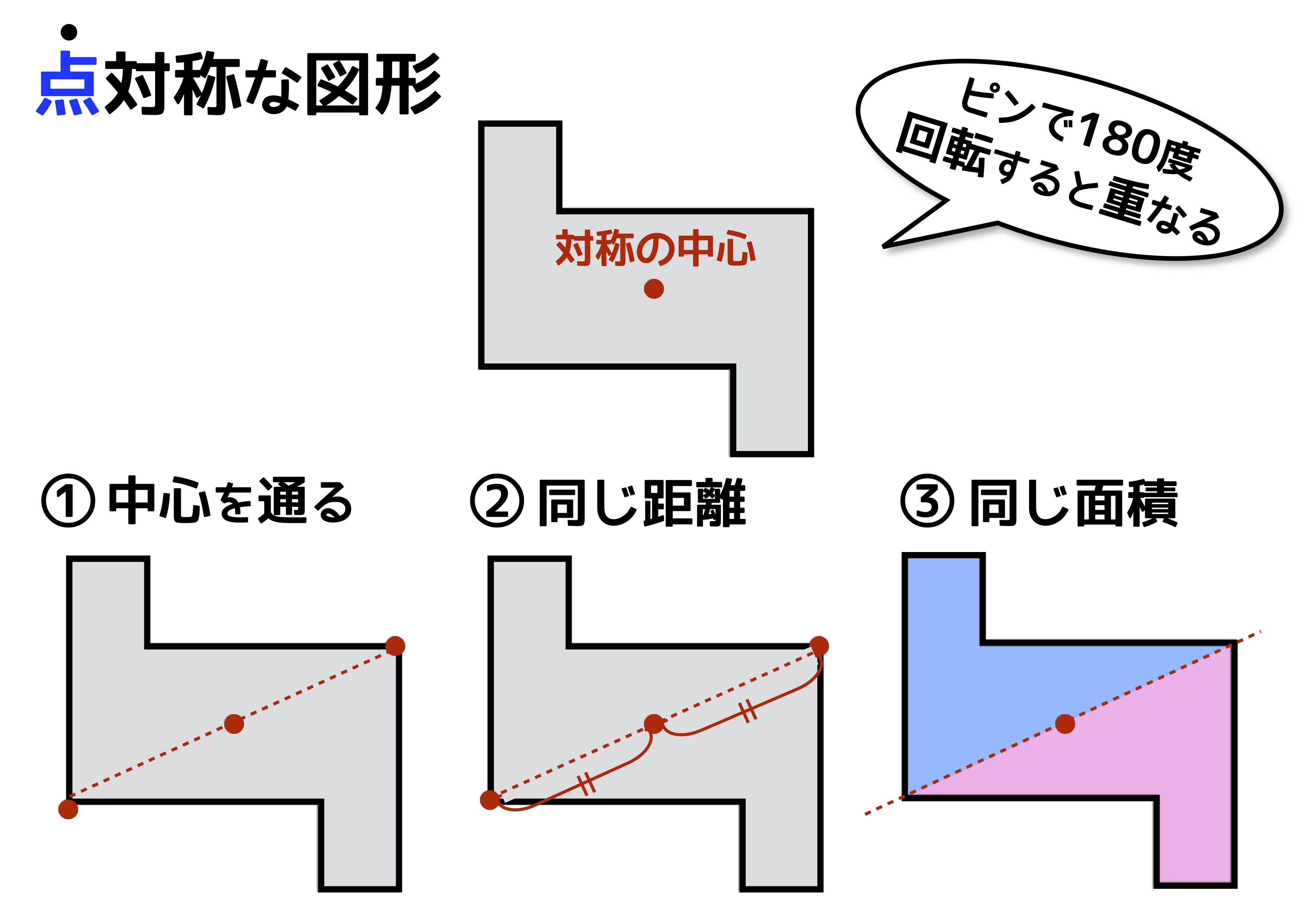
「点対称」のおさえるべき性質

続いて、点対称です。点対称は「ピンをとめて180度回転させると重なる図形」ですね。ここでいうピンのことを「対称の中心」といいます。性質も線対称と同じく3つあります。

ひとつ目は、対応する点を結ぶと必ず対称の中心を通るという性質。ふたつ目は、対称の中心から対応する点までは同じ長さであるという性質。みっつ目は、対称の中心を通る直線の両側にある対応する図形の面積は等しいという性質です。こちらも難しいことはないですね！

線対称と点対象 中学入試の出題パターン

いよいよ線対称と点対称の性質を使って問題を解くためのパターンをいくつかご紹介します。線対称と点対称、それぞれの3つの性質を頭のどこかに置いて取り組んでいきましょう。

今回は過去に実際に入試問題で出題された問題の中から4つのパターンをご紹介します。問題文に線対称や点対称という言葉が出てこないパターンもあるので、問題と格闘しながら線対称や点対称の性質を使うことに気づくことが大切ですね。

パターン1：線対称と点対称を知識として問う問題

まずはなんのヒネリもありませんが、平面図形の問題で線対称や点対称が出てくるパターンです。

「点Bは直線Lを対称の軸として点Aと線対称の位置にあります」という具合です。

問題文が自ら宣言してくれているので素直にとらえれば良いですね。問題文が宣言するということは、必ず条件として使うはず、使わなければ解けないはず！と考えましょう。

そうであれば、問題用紙の図形には、対応する点と点を直線で結んで軸と垂直に交わらせたり、同じ長さになるところをマークしたり、線対称や点対称の性質をドンドン書き込むクセをつけることが大切です。

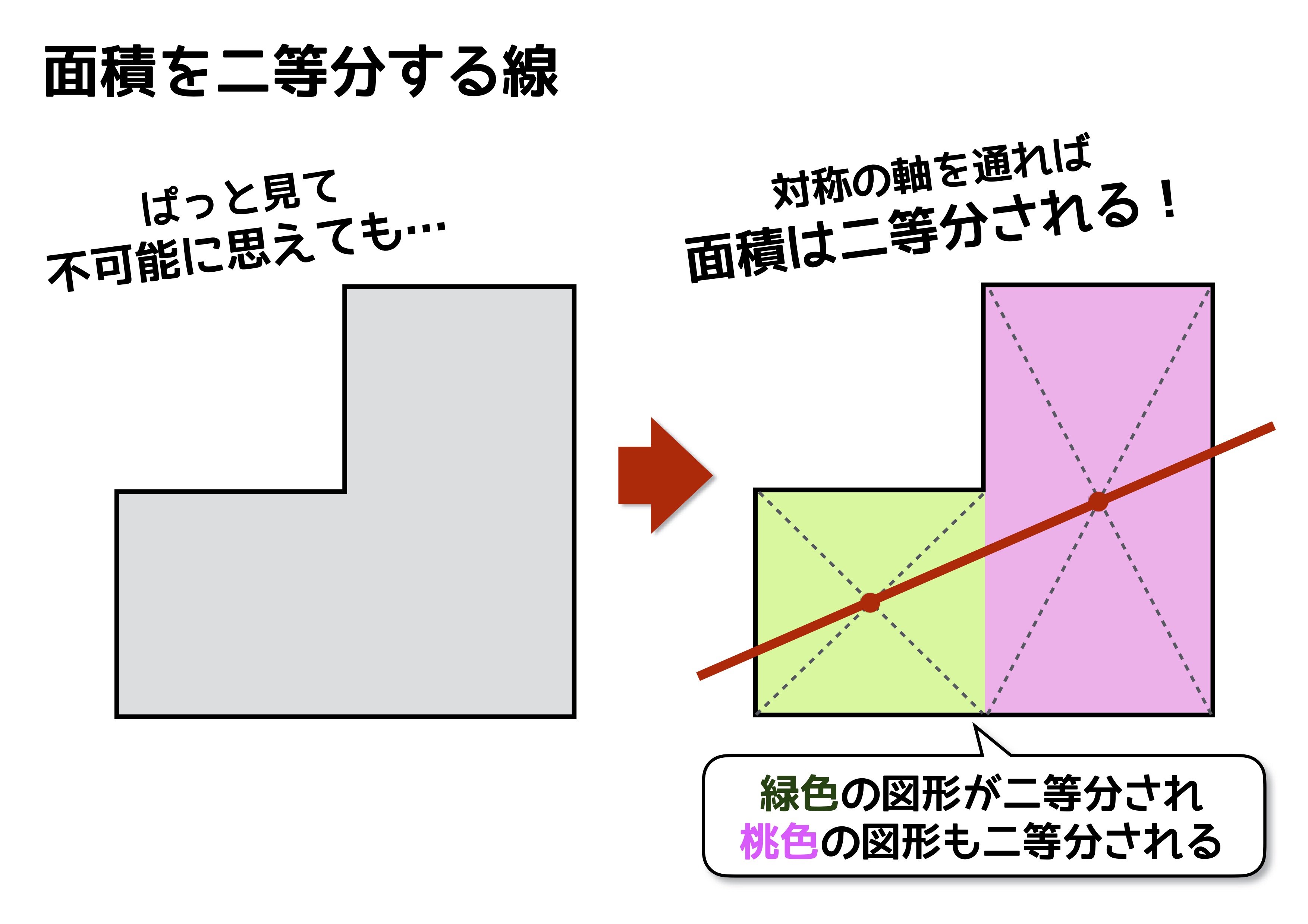
パターン2：面積を二等分する問題

次のパターンは、線対称と点対称の性質のうち、対応する図形の面積が等しくなるという性質を使った問題です。

たとえば、複雑そうに見える図形の面積を二等分する直線を作図しなさいという問題です。この手の問題は点対称の中心を見つけて、その点めがけて直線を引くという解法が有効です。点対称の中心を通りさえすれば、両側にある面積は等しくなることを利用します。

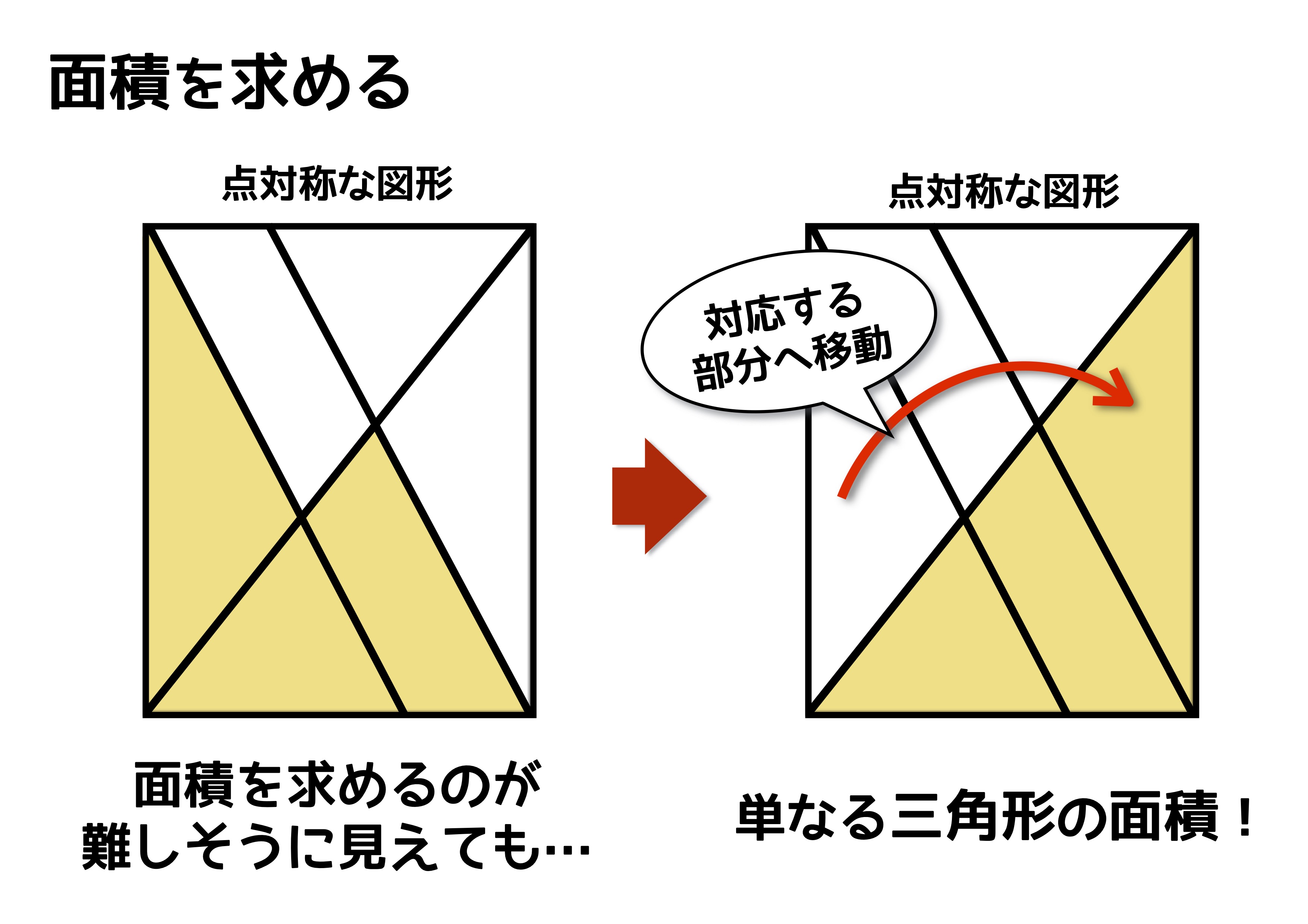
もうひとつの例題は、線対称や点対称の図形がコッソリ隠れている図形の面積を求める問題です。ぱっと見ると複雑すぎて面積を求めるのが不可能な問題のように見えるのが特徴です。しかし、対称な図形を見つけることができさえすれば一気に解けます。パズルのように等しい面積を移動してみるとシンプルな図形に変わり、簡単に計算できてしまうのです。

パターン3：鏡の反射を扱う問題

線対称の分野で王道の問題と言えば鏡の反射の問題です！ 理科の分野でも出題されることがあります。鏡の反射の問題は2つの視点で線対称をとらえてみましょう。

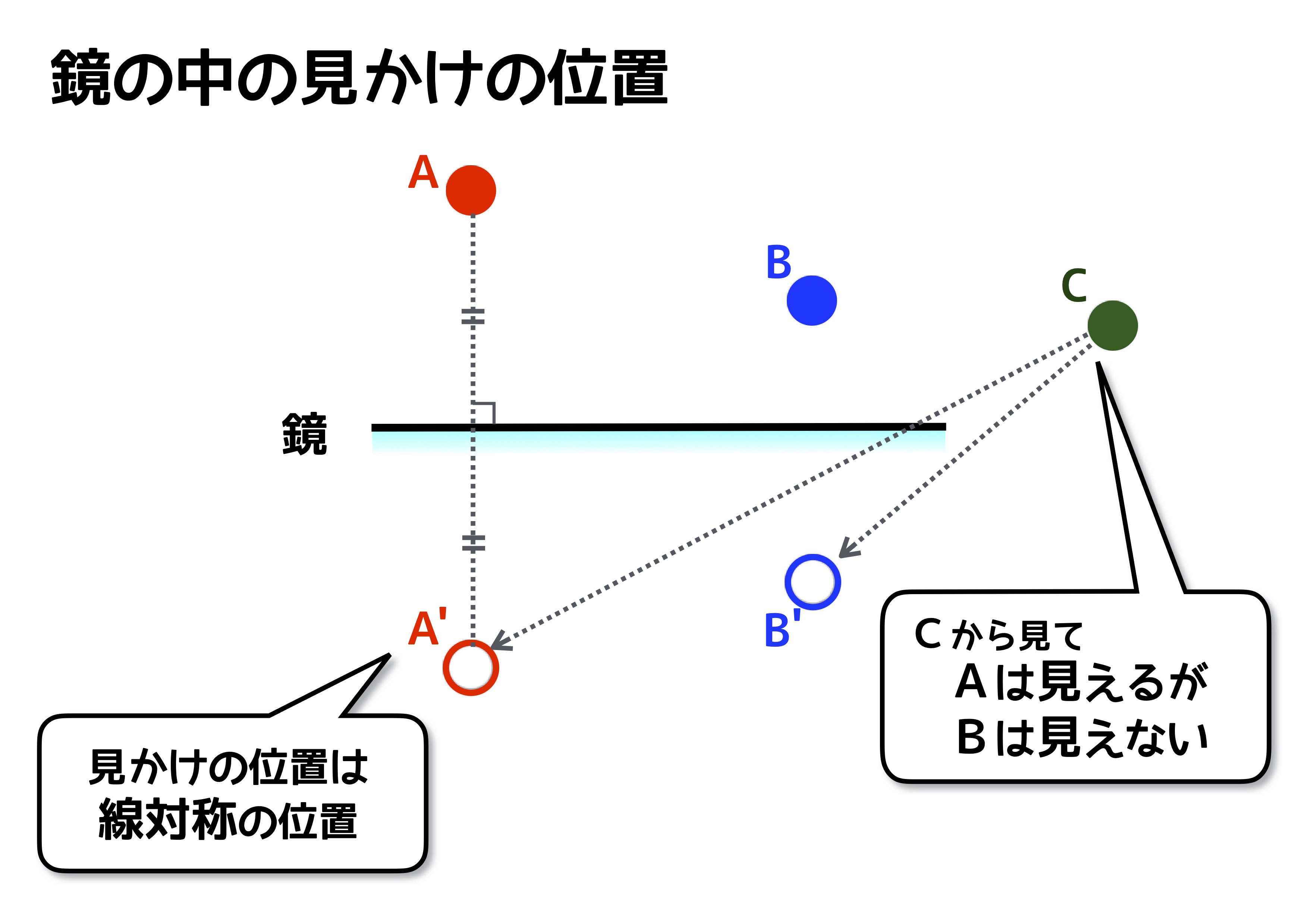
ひとつ目の観点は、見かけの位置です。鏡の前にあるものの見かけの位置は、鏡面を対称の軸として線対称の位置に見えるというものです。

鏡の前に複数の点があり、ある点から見えない点はどれか？と問われたり見かけの位置を作図しなさい。という形で出題されています。鏡面を対称の軸として線対称の作図ができれば簡単に解くことができます。

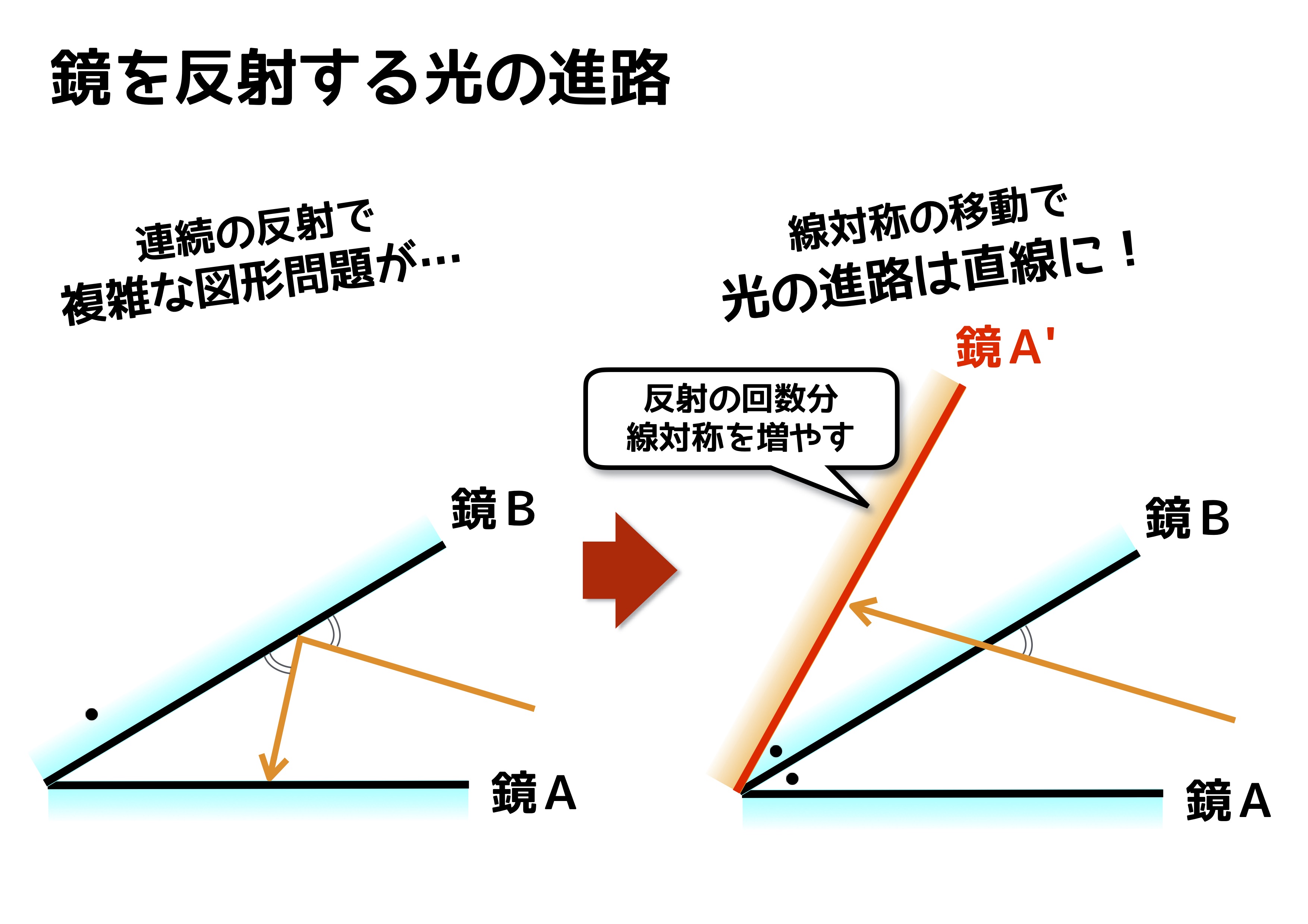
もうひとつの観点は、光が反射しながら進む進路はどうなるかというものです。光がある点から発せられ、何回か鏡に反射しながら進んでいく問題です。N回目に反射する点はどこかを問われたり、N回目に反射するまでに進んだ距離はいくらか？という形で出題されています。こちらも同様に、反射をそのままとらえると複雑なので、鏡面を対称の軸として線対称の作図をすれば光の進む道はシンプルな直線になることを利用します。

パターン4：最短距離を求める問題

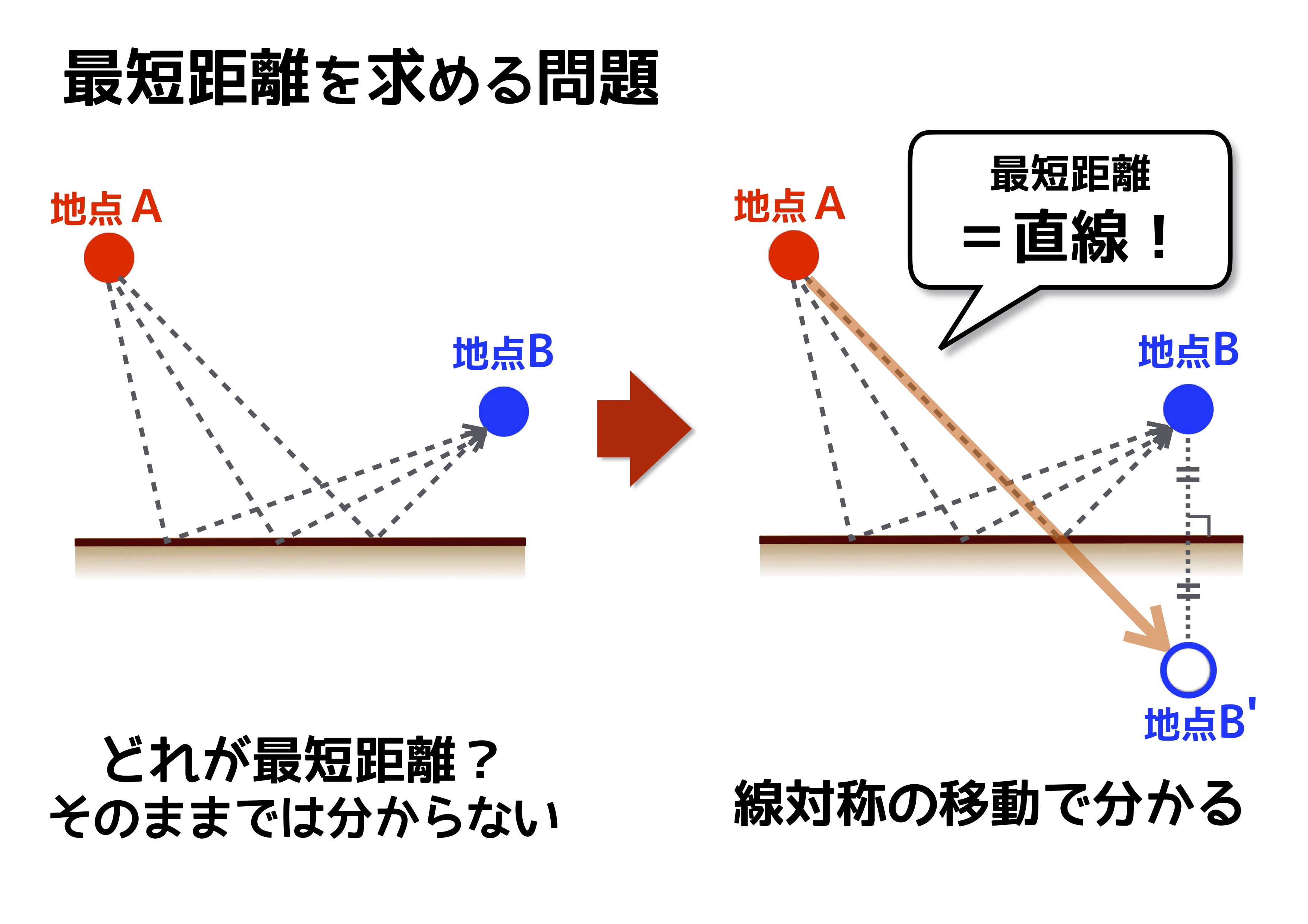
最後は最短距離を求める問題です。シンプルな例だと、ある地点から壁にタッチして、別の地点に到達しようとするときに最短距離となるために壁タッチをすべき位置はどこか？という問題ですね。

最短距離といえば直線！しかし直線を引きたくても壁にタッチしなくてはいけないのでそのままでは、直線を引くことはできません。そこで線対称を使います。

壁を対称の軸として目的の地点を線対称の位置に移動してあげれば、直線を引くことができるようになりますね。直線を引いた時に対称の軸と交わるところが、最短距離となるための壁タッチの位置となります。こちらも線対称を使う事に気づき、作図することができればとてもシンプルな問題に様変わりしますね！

まとめ

線対称と点対称は中学入試ではどのように扱われているかをご紹介しました。線対称や点対称の作図ができるだけでは中学受験対策としては不十分です。受験では線対称と点対称の性質を利用できるかが問われるためですね。そのためには、線対称と点対称が持つそれぞれ3つずつの性質をおさえたうえで、実際の受験問題で線対称や点対称を使うことに気づく練習するのが有効と言えます。

※記事の内容は執筆時点のものです