分数のわり算の仕組みを理解しよう！ 逆数をかけるのはどうして？ の謎に挑む

分数のわり算といえば、ほとんどの小学生は「逆数をかける」と答えます。しかし、「逆数をかけるのはどうして？」と聞かれると、首をかしげる小学生が多いようです。

また、「計算はできるけど、どうしてそうなるのかわからない」とモヤモヤしている小学生もいると思います。今回は、分数のわり算について、「どうして？」を詳しく解説します。

「分数÷整数」は、整数を分母にかけよう！

小学校の授業では、分数のわり算は「分数÷整数」から学びます。\(\frac{1}{3}\)÷2＝\(\frac{1}{6}\)
の ようなわり算です。このタイプのわり算は、最初のうちは、「整数を分母にかけましょう」と教わります。整数を分母にかける理由について、図を使って考えてみましょう。

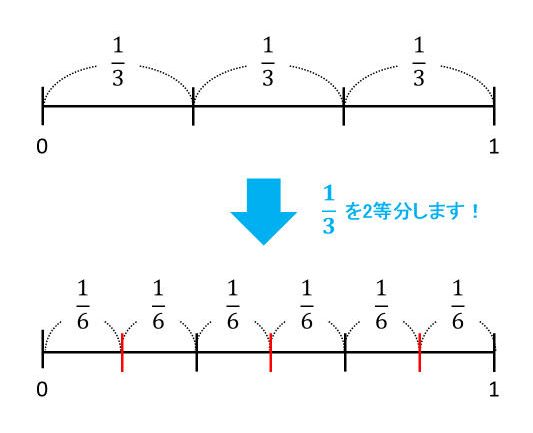
まずは\(\frac{1}{3}\)÷2＝\(\frac{1}{6}\)からです。\(\frac{1}{3}\)は、数直線上で、1を3等分したうちの1つ分で表せます。

この\(\frac{1}{3}\)を2等分していくと、1を6つに分けたことになります。たしかに、2を分母の3にかけた結果と同じです。

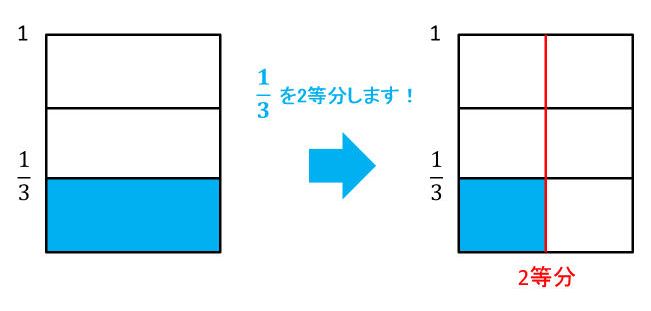
数直線ではなく、面積図を使って考えてもいいでしょう。全体を1と考えると、縦に3等分したところが\(\frac{1}{3}\)です。これをさらに横に2等分すると、次の図から\(\frac{1}{6}\)だとわかります。

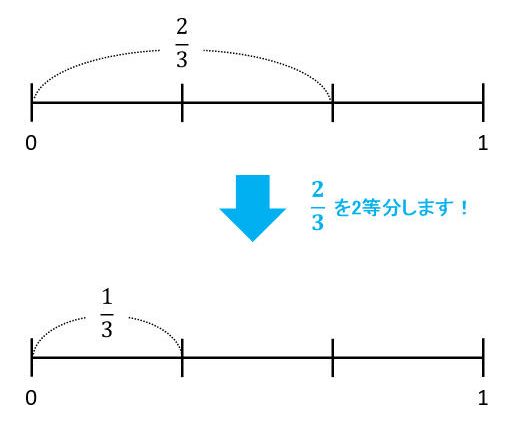
次に、約分が必要な\(\frac{2}{3}\)÷2＝\(\frac{1}{3}\)も見てみましょう。\(\frac{2}{3}\)は、数直線上で、1を3等分したうちの2つ分で表せます。この\(\frac{2}{3}\)を2等分すると\(\frac{1}{3}\)になることは、数直線を見れば明らかです。

数直線や面積図で考えれば、「分数÷整数」の計算方法を理解できます。しかし、これだけでは、「分数÷分数」を計算できません。そこで、逆数をかける計算方法が登場します。

「分数×分数」は、逆数を使ってかけ算に直そう！

「分数÷分数」の計算は、÷の後ろを逆数にすることでかけ算に直せます。たとえば、\(\frac{5}{7}\)÷\(\frac{2}{3}\)=\(\frac{5}{7}\)×\(\frac{3}{2}\)=\(\frac{15}{14}\)です。この計算方法を、「分数÷整数」のように数直線や面積図を使うのではなく、これまで学んできたかけ算やわり算の知識を使って説明してみましょう。

割られる数と割る数に同じ数をかける考え方

余りの出ないわり算は、割られる数と割る数に同じ数をかけて計算した結果ともとの計算結果は等しくなります。