倍数算はどうやって解くの？ 線分図や比例式を使って比の応用問題を攻略しよう

比の応用問題に「倍数算」があります。倍数算とは、2つの数が増えたり減ったりするとき、変化前の数や変化後の数などを求めるタイプの問題のことです。

なぜ「倍数」なのかというと、変化前の数と変化後の数を最小公倍数でそろえるからです。この説明だけだとわかりにくいので、いくつかの問題を例にして、倍数算の解法について解説します。

増減が同じになる問題を解いてみよう

この問題は、姉があげたおはじきの個数と、妹がもらったおはじきの個数が同じです。このように増減が同じになる問題では、数字だけの表で表されることがあります。しかし、それだけだとイメージしにくいので、先に線分図を使った解法を紹介しましょう。

倍数算を線分図で表してみよう

問題文を線分図で表すと次の通りです。

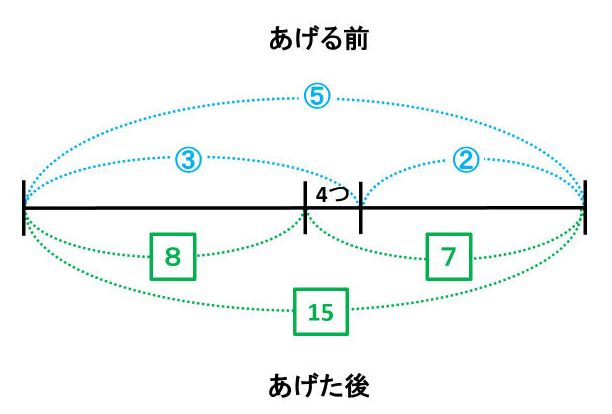
線分の上の丸で囲まれた数字が、姉が妹におはじきをあげる前のおはじきの比です。

一方、線分の下の四角で囲まれた数字が、あげた後のおはじきの比です。

この線分図からわかるのは、丸で囲まれた比の5と、四角で囲まれた比の15が、同じ個数を表しているということです。

そこで、次のように、5と15を最小公倍数の15にそろえます。

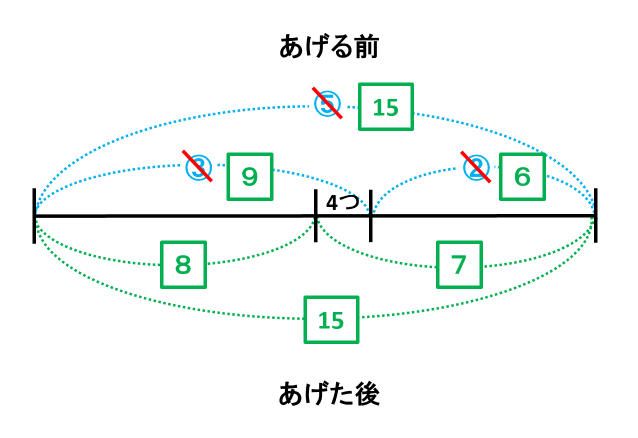
すべての比が四角でそろったところで、比の1（9－8）に当たる個数が4つだわかります。したがって、今、妹がもっているおはじきは比の7なので、4×7＝28（個）です。