
天秤算で食塩水の濃度問題を攻略! 食塩水の重さと濃度の関係を逆比で考えよう
中学受験算数では、割合の一分野として食塩水の濃度(濃さ)を扱います。
そもそも「濃度(濃さ)」とは、食塩水の重さを100%としたとき、溶けている食塩の重さが何%に当たるかを表しています。たとえば、300gの食塩水に60gの食塩が溶けていれば、\frac{60}{300}×100=20(%)です。
このように単純な濃度計算は簡単です。しかし、異なる濃度の食塩水を混ぜ合わせたり、食塩水から水を蒸発させたりとなると、苦手とする受験生が一気に増えます。そんな受験生の役に立つのが天秤算です。今回は、天秤算が成り立つ理由から実際の使い方までを解説します。
Contents [hide]
- 天秤算の正体は、面積図を使った解法!
- 天秤算を使って、さまざまな食塩水の問題を解いてみよう!
- 水を加える問題
- 水を蒸発させる問題
- 食塩水の一部をこぼして水を加える問題
- 天秤算は、慣れるととても便利な道具になる!
天秤算の正体は、面積図を使った解法!
次の混ぜ合わせの問題を考えてみましょう。
3%の食塩水40gと9%の食塩水200gを混ぜ合わせると、何%の食塩水になりますか。
天秤算を理解するためには、まずは面積図を使った解法を理解する必要があります。
濃度の問題では、縦を濃度、横を食塩水の重さ、面積を食塩の重さとする長方形を描きます。面積図を使って解く場合、具体的に食塩の重さを求める必要はありません。そのため、縦の濃度は%のままで大丈夫です。
実際に問題を面積図で表すと次の通りです。
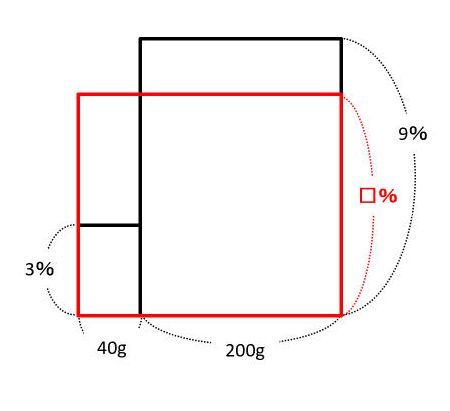
上の図では、2つの長方形のでこぼこをならした赤い長方形の縦が、求める濃度になります。この面積図では、次のように長方形Aと長方形Bに注目します。
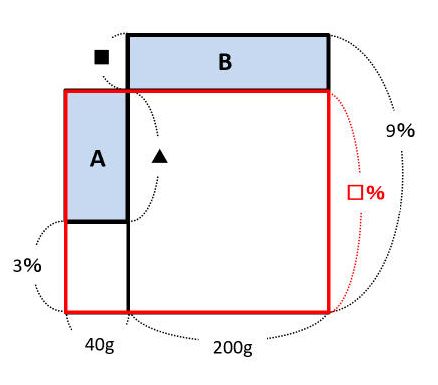
2つの長方形のでこぼこをならしたのですから、長方形Bが長方形Aの位置に移動したと考えられます。したがって、(長方形Aの面積)=(長方形Bの面積)です。
これを式に表すと▲×40=■×200なので、比の形に直すと▲:■=200:40=5:1です。
また、▲+■=9-3=6より、▲=6×\frac{5}{5+1}=5です。
求める濃度(□%)は、3+5=8(%)です。
以上の計算を、てこの原理の問題と同じように考えるのが天秤算です。この天秤算では、長方形Aと長方形Bを次のような天秤で表します。
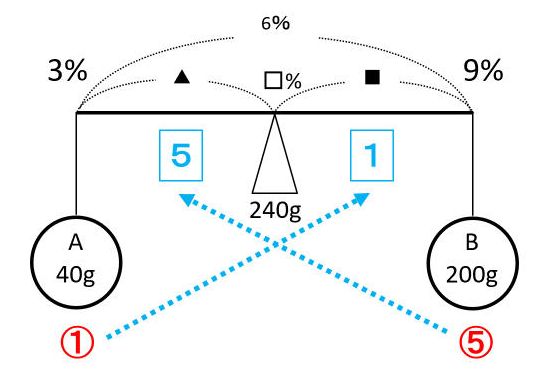
てこの問題では、おもりの重さと支点までの腕の長さは逆比の関係になります。
同じように、天秤算でも、食塩水の重さと濃度は逆比の関係になります。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

