
マッチ棒の問題をどう解くか? 図形と規則性の関係に注目すれば難しくない
マッチ棒の問題というと、マッチ棒を何本か動かして元の図形の形を変えるマッチ棒パズルが有名です。しかし、中学受験で出るマッチ棒の問題はほとんどが規則性に関する問題で、パズルのような発想を必要としません。苦手な受験生のために典型問題の解き方を解説します。
Contents [hide]
- マッチ棒の問題は等差数列?
- マッチ棒の問題の応用は難しい?
- N番目の図形と縦や横の本数を数える問題
- N番目の本数が等差数列の和になる問題
- マッチ棒の問題は中学数学にも出る
マッチ棒の問題は等差数列?
マッチ棒をある「きまり」に従って並べる問題では、最初に等差数列の可能性を考えましょう。
マッチ棒で三角形を作っていく問題
【問1】下の図のようにマッチ棒を並べていきます。三角形を100個作るとき、マッチ棒を何本使いますか。
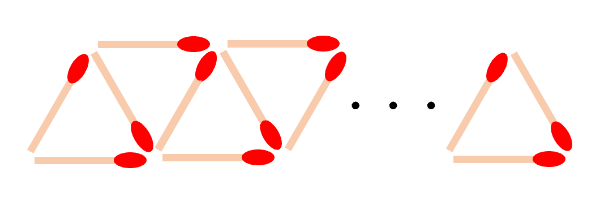
マッチ棒の問題では、実際にマッチ棒の本数を数えてみることが大切です。与えられた図から、三角形が1個、2個、3個、4個のときのマッチ棒の本数を次のように書き出してみました。
- 三角形が1個 … マッチ棒が3本
- 三角形が2個 … マッチ棒が5本
- 三角形が3個 … マッチ棒が7本
- 三角形が4個 … マッチ棒が9本
三角形が1個増えると、マッチ棒が2本増えることがわかります。これは、初めの数が3、加える数が2の等差数列です。
等差数列のN番目の数は次の公式で表せます。
N番目の数=初めの数+加える数×(N-1)
三角形を100個作るときのマッチ棒の本数を求めるのは、100番目の数を求めるのと同じなので、公式に当てはめて3+2×(100-1)=201(本)が答えです。
マッチ棒で正方形を作っていく問題
【問2】下の図のようにマッチ棒を並べていきます。マッチ棒を220本使うとき、正方形は何個作れますか。
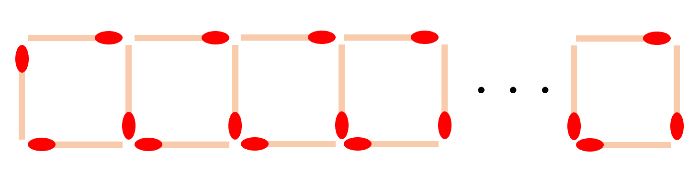
【問1】と同じように数えると、正方形が1個増えると、マッチ棒が3本増えることがわかります。初めの数が4、加える数が3の等差数列と考えて、正方形をN個作るときのマッチ棒の本数は4+3×(N-1)です。これが220本になればよいので、4+3×(N-1)=220として逆算でNを求めます。N=(220-4)÷3+1=73(個)が答えです。
マッチ棒の問題の応用は難しい?
図形が1個ずつ増えていくのではなく、より複雑な増え方をするマッチ棒の応用問題もあります。こういう問題を解くときの発想を学びましょう。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます


