
流水算の解き方をわかりやすく解説! ダイヤグラムや比を使って速さの応用問題を解く
多くの中学受験生が5年後半に学ぶ速さの応用に流水算があります。基本問題の解き方はパターンが決まっているものの、複雑な応用問題もよく出るので、苦手とする受験生も多いでしょう。そんな流水算の基礎を確認した上で、少し難しい問題を丁寧に解説します。
Contents [hide]
- 流水算の基本を理解する
- 流水算の応用問題を解く
- 船のエンジンが故障する問題
- エスカレーターの問題
- 流水算は受験生の盲点になりやすい
流水算の基本を理解する
流水算とは、川を進む船の速さなどを求める速さの問題です。流水算で使う言葉や線分図を理解することが大切です。
流水算で使う言葉
川の水は上流(川上)から下流(川下)に流れます。ダイヤグラム(グラフ)がある場合、上が上流で下が下流とは限らないので要注意です。問題文や直線の傾きからグラフの上流と下流を決めましょう。
また、川の流れがないところを船が進む速さを「静水時の速さ」といいます。一方、下流から上流に進む速さは「上りの速さ」で、上流から下流に進む速さは「下りの速さ」です。これらの速さには次の関係があります。
- 上りの速さ=静水時の速さ-川の流れの速さ
- 下りの速さ=静水時の速さ+川の流れの速さ
流水算で使う線分図
流水算で使う線分図は他の速さの問題と異なります。次の問題で線分図の意味と使い方を理解しましょう。
【問題1】一定の速さで流れる川を船が進むとき、上りの速さは時速22km、下りの速さは時速28kmでした。この船の静水時の速さと川の流れの速さを求めなさい。
流水算では、3本の線分図を描きます。下の図のように、それぞれの線分は上りの速さ・静水時の速さ・下りの速さを表します。線分が道のりを表すわけではないので要注意です。
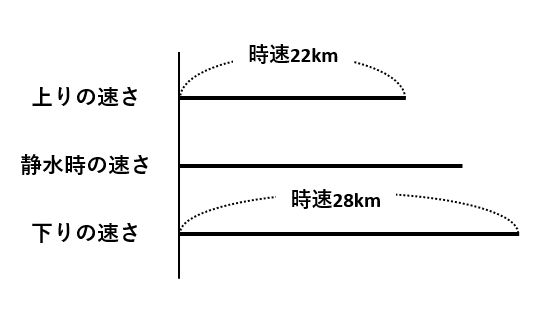
問題文に「一定の速さで流れる川」とあるので、「静水時の速さと上りの速さの差(ア)=下りの速さと静水時の速さの差(イ)=川の流れの速さ」です。
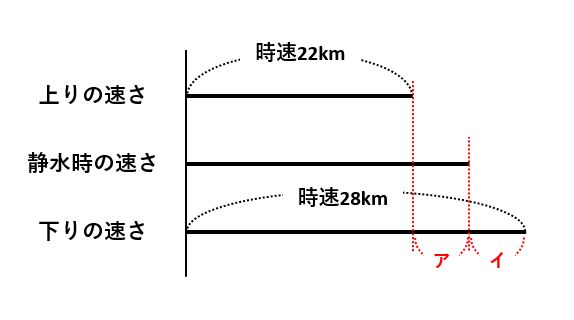
したがって、「川の流れの速さ=(下りの速さ-上りの速さ)÷2」が成り立ち、川の流れの速さは(28-22)÷2で時速3kmと求められました。
また、「静水時の速さ=上りの速さの差+川の流れの速さ」より、船の静水時の速さは時速25kmです。
流水算の応用問題を解く
流水算には、船のエンジンが故障する問題や、エスカレーターの問題もあります。これらの応用問題ではダイヤグラムや比が役立ちます。
船のエンジンが故障する問題
【問題2】川下のA地点を出発した船が、72km離れた川上のB地点に到着するのに、いつもなら3時間かかります。ある日、この船が8時30分にA地点を出発しましたが、途中でエンジンが停止して川に流されました。10分後にエンジンの修理が終わって再びB地点へ向かい、11時43分にB地点に到着しました。このとき、川の流れの速さと船の静水時の速さはそれぞれ時速何kmですか。ただし、どちらの速さも一定であるとします。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます


