
ニュートン算ってどんなもの? ニュートン算をわかりやすく解説
中学受験に向け算数で学習するもののひとつに「ニュートン算」があります。受験をしないと耳慣れない言葉ですが、受験生は全員解けるようになるべき単元です。そこで、今回はニュートン算の解法とつまずきやすいポイントについて解説します。
Contents [hide]
ニュートンとは? 中学受験ではどのような扱い?
ニュートン算とは、「特定の場所に一定の数量が入り、同時に一定の数量が出て行くという条件のもと、特定の場所がある数量になる時間を問う」という問題です。抽象的な説明ではよくわからないので、例をみてみましょう。
■ニュートン算の例1
映画館のチケットを買う列に、今50人の客が並んでいます。1分間で、列にはあらたな客が5人並び、窓口では10人にチケットを売ります。列がなくなるのは何分後でしょうか。
■ニュートン算の例2
ある水そうに水が20L入っています。水道のじゃ口から毎分12Lの水を水そうに注ぎ入れながら、1台のポンプで毎分14Lの水をくみ出すと、何分後に水そうは空になりますか。
ニュートン算は「仕事算」や「速さ」の応用問題であり、学習塾では主に小学6年生で習います。頻出とまではいきませんが、出題された場合、解法がわからないと解くのに手間取ってしまいます。そのため、基本的な解き方はしっかりとおさえておく必要があります。
ニュートン算の基本的な解き方解説
■例題
ある水そうに水が450L入っています。水道のじゃ口から毎分24Lの水を注ぎ入れながら、1台のポンプで毎分39Lの水をくみ出すと、何分後に水そうは空になりますか。
まずは、状況を図に描いてみます。線分図のように決まった形があるわけではないので、お子さんがイメージしやすいものであれば、どのような図でも構いません。
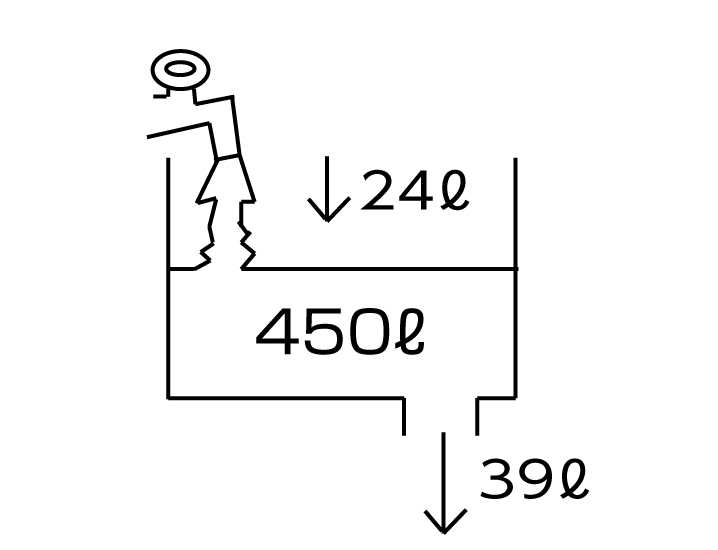
【図1】
図を見ると、1分間に減る水の量は
39−24=15(L)
になります。
全部で450Lの水が空になるには
450÷15=30分
かかります。
答え.30分
ニュートン算で子供がつまずきやすいポイントとその対策
子供がつまずきやすいポイントは、以下の3つです。
[1]「ひき算する」発想がない
[2]問題文が変わると解けなくなる
[3]ニュートン算の応用問題に対処できない
それぞれの対策を見ていきましょう。
[1]「ひき算する」発想がない
ニュートン算では、1分間に一定の数量が出たり、入ったりします。その結果として「水そうに水が溜まる」、あるいは「水そうから水が抜ける」わけです。
こういった状況自体は、お子さんも比較的理解がしやすいと思います。はじめはわからなくても、図を描けば「そういうことか」と納得できます。
しかし、問題はその先です。「変化の量」が「出ていく量」と「入ってくる量」の差(=ひき算)で求められるということがわからないことがあるのです。もし、ここでつまずいてしまったときは、以下のような簡単な図でお子さんに説明してあげましょう。
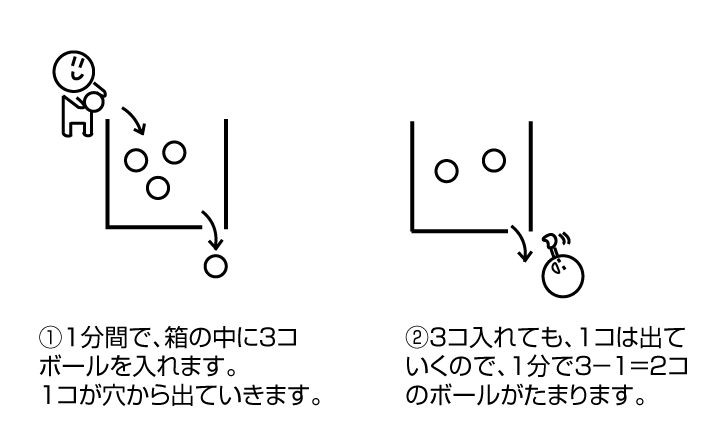
【図2】
このような簡単な図で原理がわかるようになれば、水量や人数でも計算できるようになります。
[2]問題文が変わると解けなくなる
ニュートン算でよく出題されるのは、冒頭で例に挙げた水そうの問題と、列に並ぶ問題です。最低でも、この2種類の問題は解いてみましょう。「ある数が入って、出ていく問題 → ニュートン算」というイメージができるようになれば、場面が変わっても対処可能です。
[3]ニュートン算の応用問題に対処できない
ニュートン算の応用問題では、入る数や出ていく数が複数になり、状況がイメージしづらくなります。ここで重要になってくるのが「わかりやすい図」です。図で状況を整理できれば、計算方法はいつもと同じです。簡単な問題を解くときも、必ず図を描くクセをつけておきましょう。
ニュートン算は今まで習ってきた単元の応用問題です。塾では小学6年生で習うこともあり、解けないと「受験に間に合うかな?」と思ってしまいがちな分野でもあります。しかし、焦りは禁物です。基礎からしっかり復習しましょう。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

