分数を小数に直すには？ 分数の計算でよく使う「基本知識」で簡単に理解しよう

中学受験の算数で避けて通れないのが、「分数から小数への変換」、そして「小数から分数への変換」です。分数や小数の計算は苦手な子が多いですが、分数の計算でよく使う「基本知識」を押さえると、簡単に理解することができます。中学生や高校生になっても頻繁に使う基本知識なので、小学生のうちからしっかり理解しておきましょう。

「分数から小数」「小数から分数」は、同じ考え方で計算できる

分数から小数への変換、小数から分数への変換……、2種類の計算のやり方があるように思いますよね。しかし、分数における「基本知識」を知っていると、両方の変換を同じ考え方で計算できます。その計算方法の紹介のまえに、まずは一般的な参考書に書かれている計算方法を紹介します。

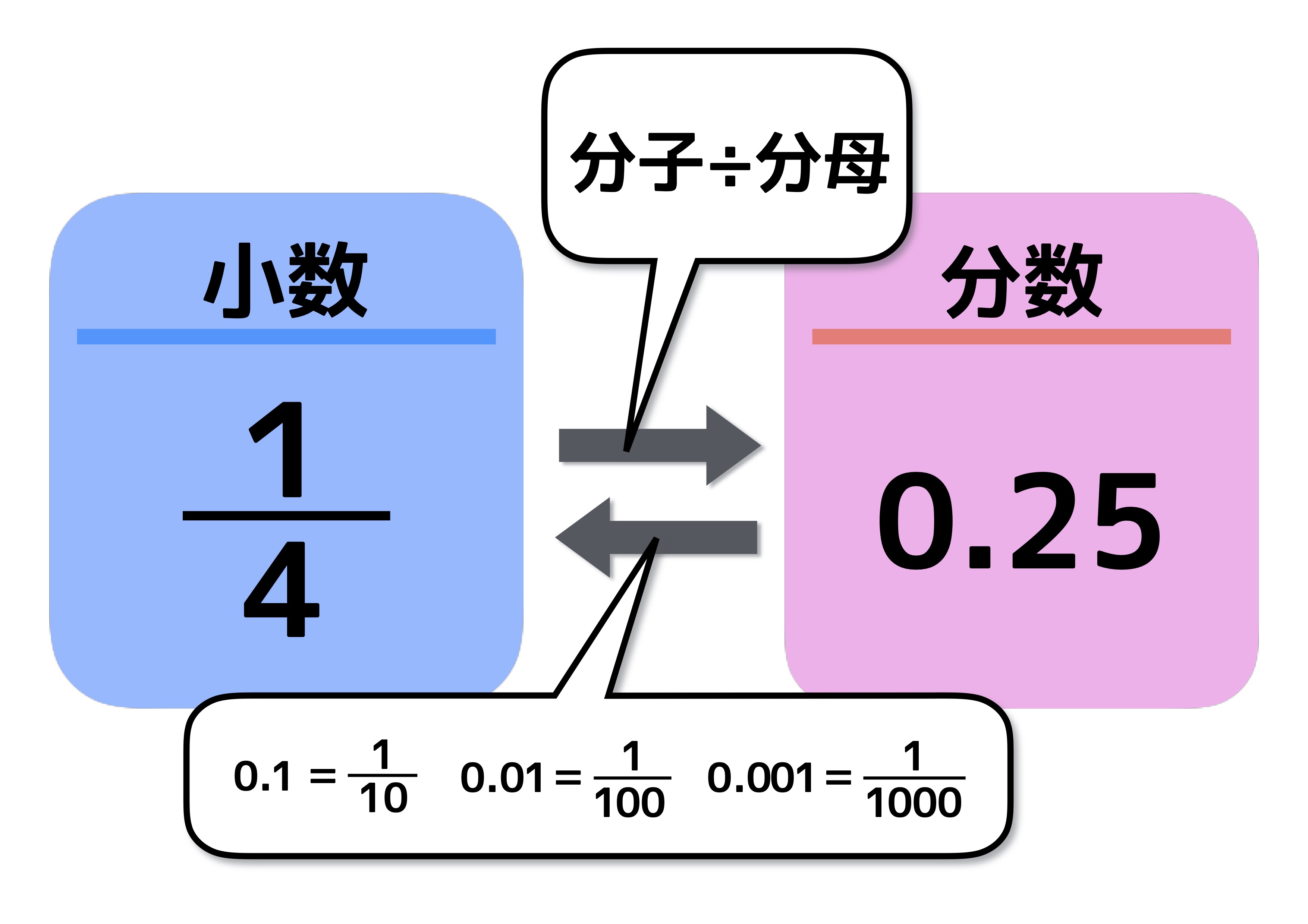
一般的な参考書による解説

分数から小数に変換する方法は、一般的には「分子÷分母」を計算する方法が解説されています。シンプルでわかりやすいため、この覚え方でも問題ありません。

一方で、小数から分数に変換する方法は、「0.1＝\(\frac{1}{10}\)」であることや、「0.01＝\(\frac{1}{100}\)」であることを利用した解説が多いようです。しかしながら、この考え方だと、子供がケタ数のミスをしてしまうことがあります。

それでは、小数と分数の変換をよりスッキリ理解するために必要な、「分数の基本知識」について紹介します。

「分数の基本知識」とは？

その基本知識とは、分数の分子と分数に同じ数を掛けたり、同じ数で割ったりすること。そして、この方法をおこなっても、分数の値が変わらないことです。ちなみに、中学生以降の数学でもよく使う基本的な方法です。

上の例では、\(\frac{2}{5}\)の分子と分母に同じ2を掛けて\(\frac{4}{10}\)にしています。\(\frac{2}{5}\)も\(\frac{4}{10}\)も同じ値ですね。同様に\(\frac{2}{6}\)は、分子と分母を同じ2で割って\(\frac{1}{3}\)にしています。\(\frac{2}{6}\)も\(\frac{1}{3}\)も同じ値です。

分数を小数に変換…分母と分子を同じ数で割る

まずは、「分数を小数に変換するケース」を考えてみます。結論からいうと、分数の分母と分子を同じ数で割ると小数に変換することができます。では、どんな数で割ると小数に変換できるのでしょうか？

【例題1】\(\frac{1}{5}\)を小数に直す

\(\frac{1}{5}\)を小数に直してみましょう。分数を小数にする場合は、分母の数字で分子と分母を割ります。\(\frac{1}{5}\)の場合は、分母の「5」で割ります。分母の数字で割るのは、分母を1にするためです。

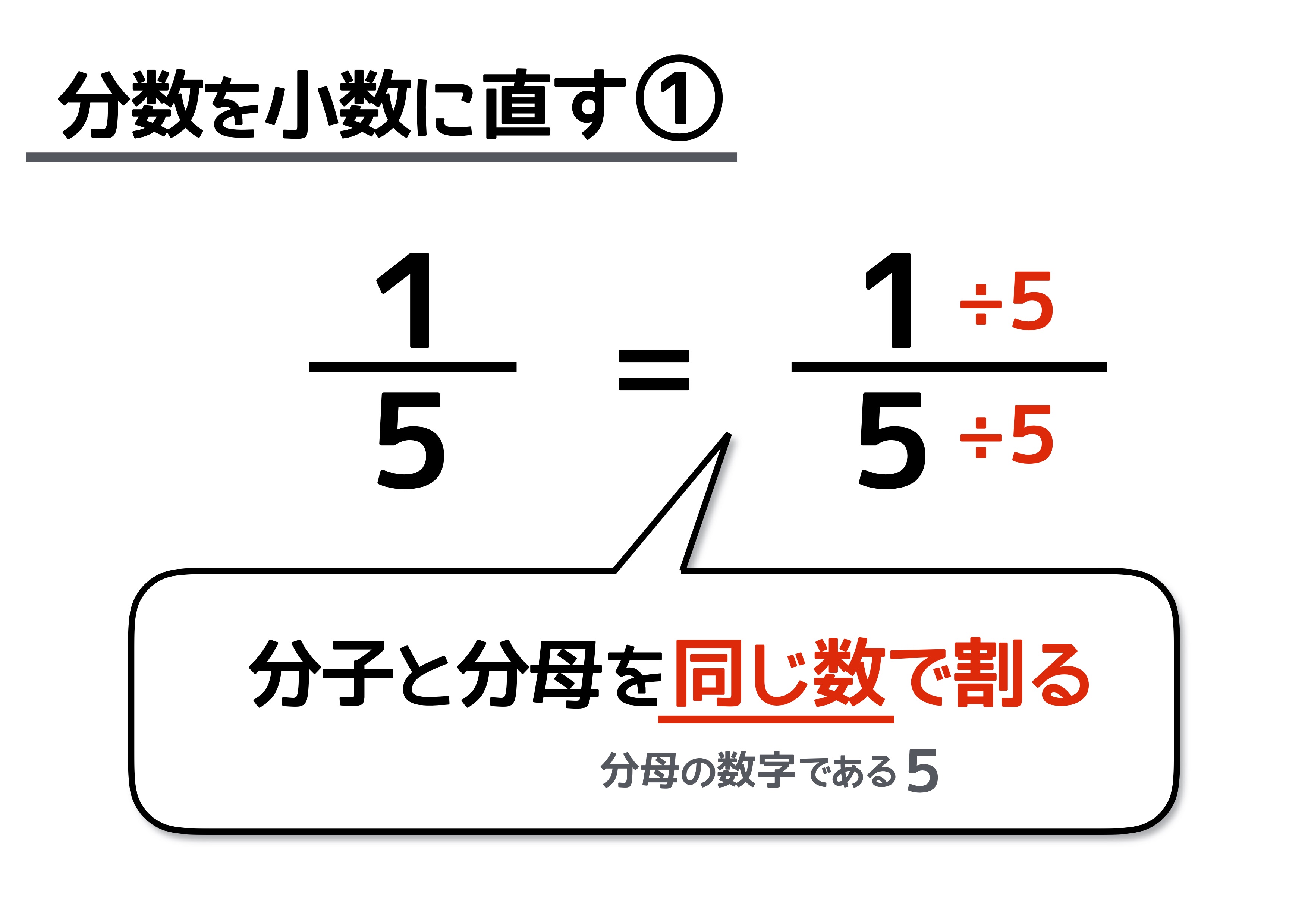
分母は「5÷5」で1になります。分子は「1÷5」なので、筆算すると、分子は0.2になります。計算の結果、分母が1の分数になりますね。つまり\(\frac{1}{5}\)は、小数に直すと0.2になります。

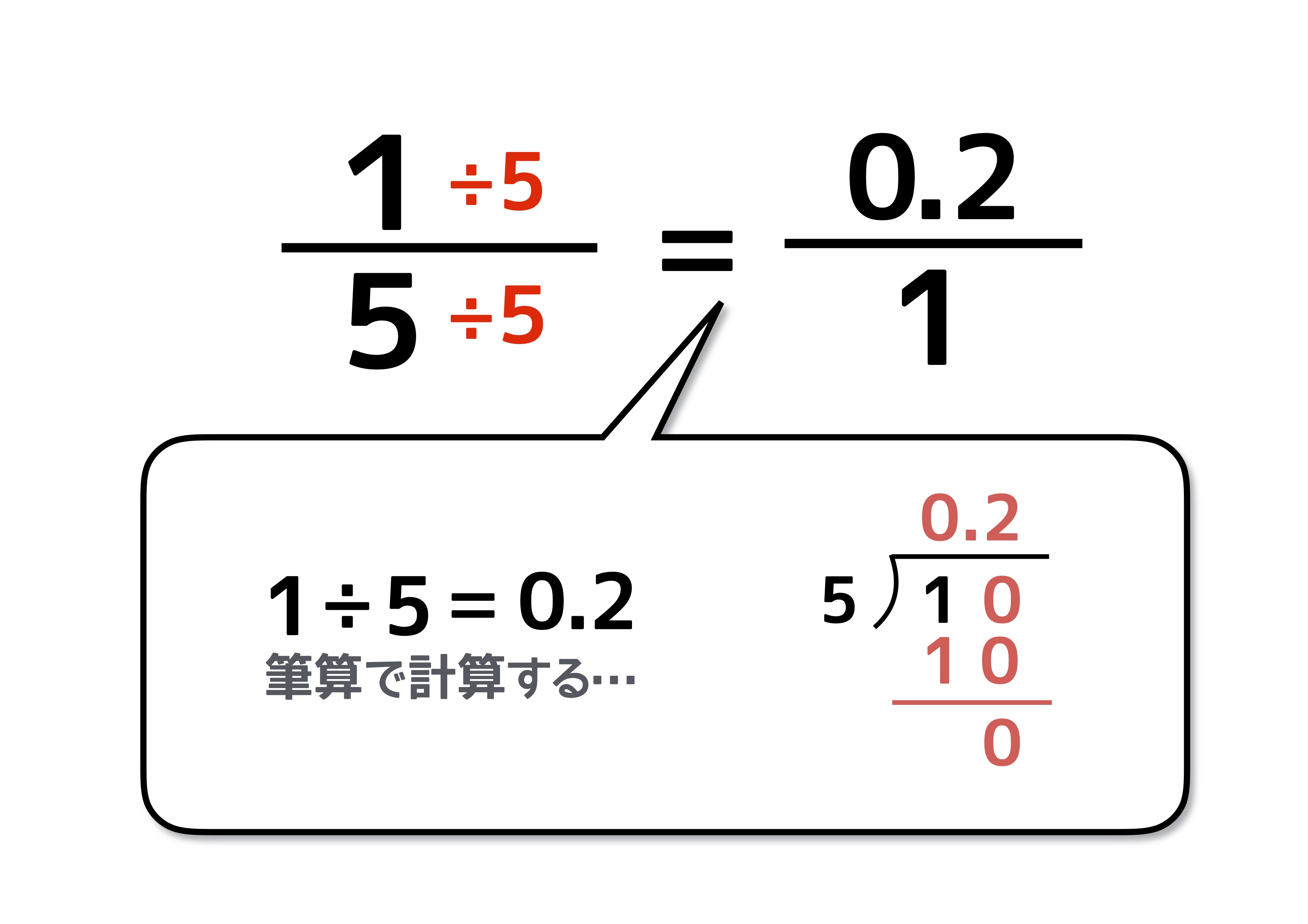
【例題2】\(\frac{3}{8}\)を小数に直す

では、\(\frac{3}{8}\)も小数に直してみましょう。まずは、分母の数字で分子と分母を割ります。分母を1にするために、分母の数字（この例では「8」）で分子と分母を割るんでしたね。すると、分母が1になります。

分子は、「3÷8」を筆算して0.375となります。この例の場合、割り算の結果が小数第3位まで続くので、計算ミスに気をつけましょう。

割り切れない場合もある

ちなみに、全ての分数を小数に直すことができるわけではありません。分母は1にできても、分子の割り算が割り切れない場合があります。この場合、分数を小数で表すことはできませんが、四捨五入して、おおよその数にすることはできます。

小数を分数に変換…分母と分子に同じ数を掛ける

つぎは、「小数を分数に変換する方法」を解説します。今度は、分母と分子に同じ数を掛けると分数に変換することができます。ところが、分子と分母に同じ数を掛けたくても、小数には分子も分母もありません。どうすればよいのでしょうか？

【例題1】0.4を分数に直す

0.4という小数を、分数に直してみましょう。まず0.4を分数で表すため、分母の部分に1を付け加えます。すると、「\(\frac{0.4}{1}\)」となります。これで分数になったように見えますね。そして、分数の分子と分母は整数である必要があるので、分母と分子に10を掛けます。

分子の「0.4×10」を計算すると、小数点が1ケタ移動するので4になります。分母は「1×10」を計算して10です。結果として、小数の0.4を\(\frac{4}{10}\)という分数の形に変換することができました。

【例題2】0.134を分数に直す

小数を分数にする例を、もう1題やってみましょう。0.134を分数に直してみます。まず、0.134には分子も分母もありませんので、分母に1を置いて「\(\frac{0.134}{1}\)」という分数の形にします。

つぎに、分子と分母に同じ数字を掛けます。0.134は小数第3位までの小数のため、10を掛けただけでは整数になりませんね。小数第3位までの小数を整数にするには、1000を掛ける必要があります。

分子の「0.134×1000」を計算すると、小数点が3ケタ移動し134に、分母は「1×1000」を計算して1000になりますね。結果として、小数の0.134を\(\frac{134}{1000}\)という分数の形に変換できました。

ケタ数の計算ミスが不安なときは？

例題1の0.4を分数にするときは、分子と分母に10を掛けるだけなので、暗算でも計算できますが、例題2の0.134は、分子と分母に1000を掛けるので計算ミスが少し心配ですよね。

掛ける数字のケタ数のミスが心配なときは、10を何回かに分けて掛けても大丈夫です。整数になるまで、何回も10を掛けるイメージですね。

まとめ

中学受験の算数で避けて通れない「分数と小数の変換」は、今回紹介したポイントを押さえると、スムーズに理解できます。改めて、以下をおさらいしましょう。

中学生や高校生で習う数学でも、この考え方はよく使われます。小学生のうちから、「分数と小数の変換」を身につけておくと良いですね。

※記事の内容は執筆時点のものです