つるかめ算はどのような問題で使えるの？ 速さ・売買損益・仕事算にも応用できる
中学受験算数の特殊算で初期に習うのがつるかめ算です。このつるかめ算はその後もさまざまな場面で登場します。
しかし、「この問題はつるかめ算だ」と気づかずに手が止まってしまうことも少なくありません。そうならないように、今回はつるかめ算の応用問題をわかりやすく解説します。
つるかめ算の基礎を復習
まずは、つるかめ算の基本問題を解いてみましょう。
【問題1】つるとかめが合わせて30匹います。足の数は合わせて84本です。つるとかめはそれぞれ何匹いますか。
つるかめ算は「つる」か「かめ」のどちらかしかいないと仮定するのがポイントです。【問題1】ではつるしかいないと仮定すると、足の数は2×30＝60本になります。一方、かめしかいないと仮定すると、足の数は4×30＝120本になります。
ここでは、かめしかいないと仮定して考えていきましょう。かめ1匹をつる1匹と交換すると、足の数は4－2＝2本減ります。同じように、かめ2匹をつる2匹と交換すると、足の数は2×2＝4本減ります。このように、かめをつるに交換していくのを表にすると次の通りです。
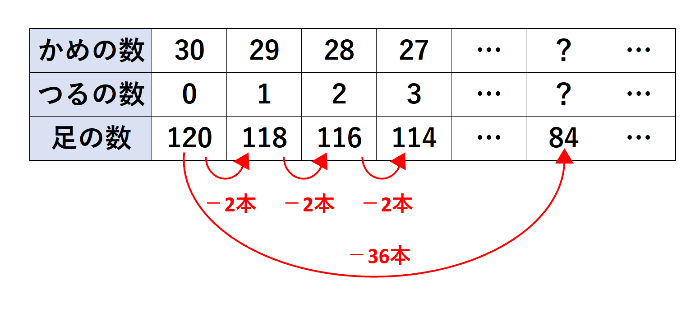
交換したときに減る足の数が120－84＝36本なので、36÷2＝18匹のかめをつるに交換したことがわかります。したがって、つるは18匹、かめは12匹です。
以上の考え方を面積図で表すこともできます。下の図のように、縦がつる1匹の足の数とかめ1匹の足の数になる長方形をそれぞれ描き、横をつるとかめの数の合計とします。
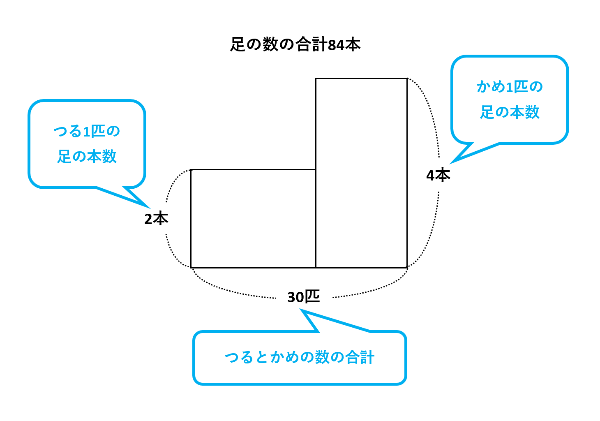
かめしかいないと仮定すると、下の図の赤い長方形を描けます。このとき、面積が36本になっている長方形は、かめをつるに交換したときに減る足の数です。したがって、つる□匹は36÷2＝18匹と求められました。
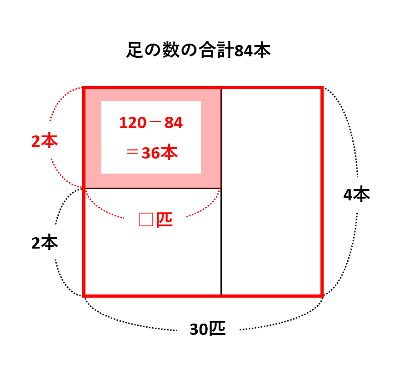
つるかめ算の応用問題を解説
つるかめ算は他の特殊算などでも使えることがあります。代表的なつるかめ算の応用問題を解説します。
速さのつるかめ算
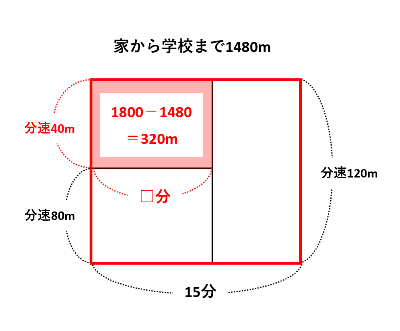
【例題2】太郎君の家から学校までは1480mです。太郎君は家を出てから分速80mで歩きましたが、途中から分速120mで走って、15分で学校に着きました。太郎君が歩いていたのは何分間ですか。
【問題2】のように、全体の道のりと時間が出ていて、途中で速さが変わる問題は「速さのつるかめ算」と呼ばれます。普通のつるかめ算と同じように考えて解いてみましょう。
面積図を描きます。下の図のように、縦が歩く速さと走る速さになる長方形をそれぞれ描き、横を時間とします。
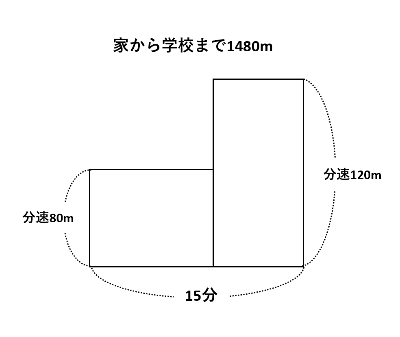
分速120mでずっと走っていたと仮定すると、下の図の赤い長方形を描けます。このとき、面積が320mになっている長方形に注目して、歩いていた時間□分は320÷40＝8分です。
売買損益のつるかめ算
【問題3】1個あたり80円で仕入れた商品150個に、5割の利益を見込んで定価をつけて売りました。次の日、定価の2割引で売ったところすべて売れて、利益の合計は5280円になりました。定価で売れた商品は何個ですか。
【問題3】のように、売上や利益の合計と売れた個数が出ていて、途中で売り値を変える売買損益の問題はつるかめ算の考え方を使えます。
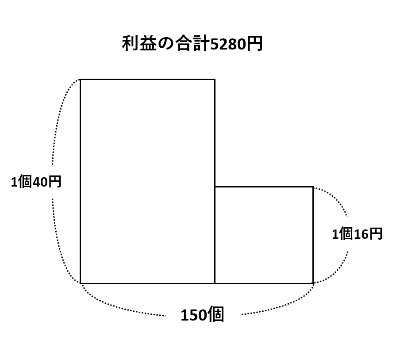
面積図を描きます。下の図のように、縦が商品1個を定価で売ったときの利益（80×0.5＝40円）と、定価80+40＝120円から2値引きして売ったときの利益（120×0.8－80＝16円）になる長方形をそれぞれ描き、横を個数とします。【問題3】は利益の合計が与えられていて、2割引で売っても損は出ていないので、売上で考える必要はありません。
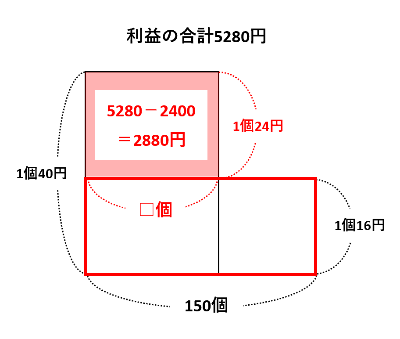
150個すべてを定価の2割引で売ったと仮定すると、下の図の赤い長方形を描けます。このとき、面積が2880円になっている長方形に注目して、定価で売った個数□個は2880÷24＝120個です。
仕事算とつるかめ算
【問題4】Aさんが1人ですると10日、AさんとBさんが2人ですると6日かかる仕事があります。この仕事をAさんが1人でした後、Bさんに代わったところ、12日かかりました。Aさんが仕事をしたのは何日ですか。
中学受験ナビについて
中学受験ナビは
保護者のための中学受験情報サイトです
会員登録すると・・・
- 中学受験のノウハウ
- お子さまに合った学校選び
- 保護者の関わり方・考え方
- 教科ごとの学習ポイント
などすべての会員コンテンツが読み放題！
毎月情報
掲載！！
通常
880円/月（税込）
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます