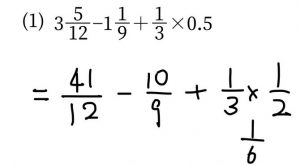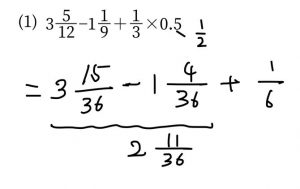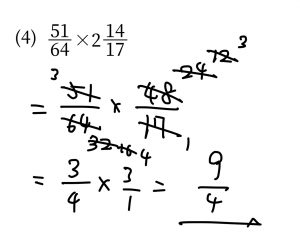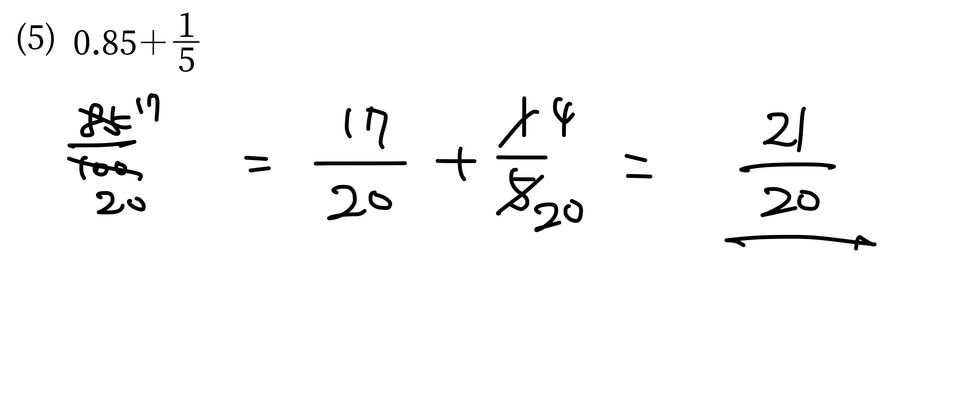計算の基礎力の「のびしろ」を見つける｜中学受験算数の基礎力を伸ばす#6

こんにちは。ドリさんです。

今回は「計算の基礎力」についてお伝えいたします。
計算力は中学受験算数で最も大事な力です。
しかし、計算力が大事だとはわかっていても、どう鍛えて良いかわからないお子様・ご家庭が多いと思います。

この記事では、「計算力」が十分についていないお子様がどう計算力をつければ良いのか、以下の順番でお伝えします。

計算の答案からのばすべきところを見つける

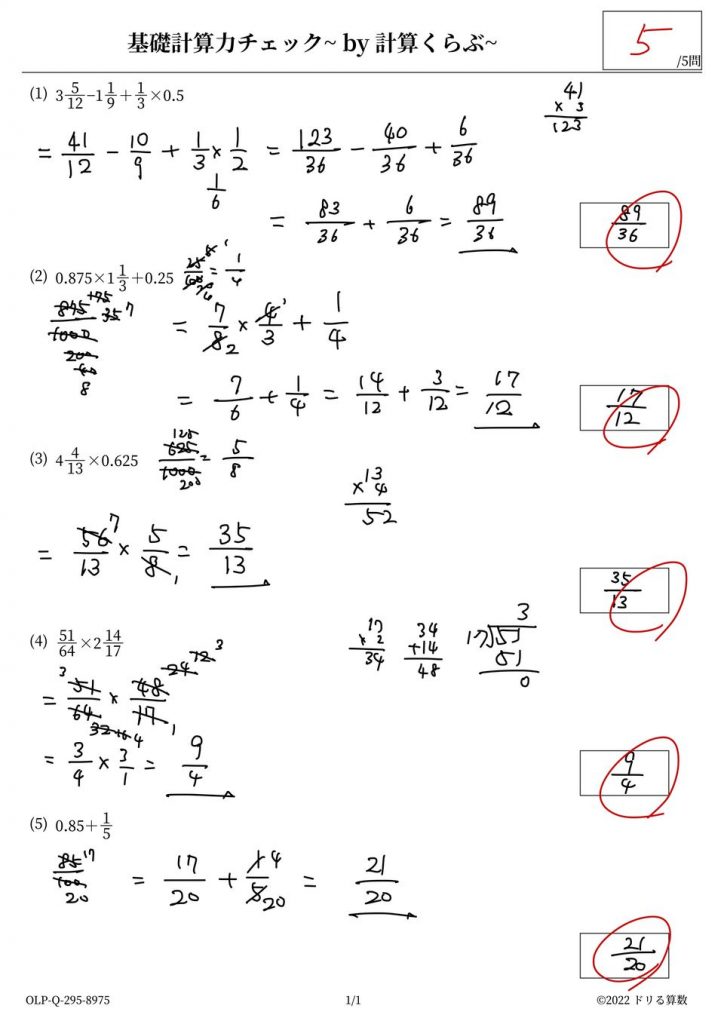
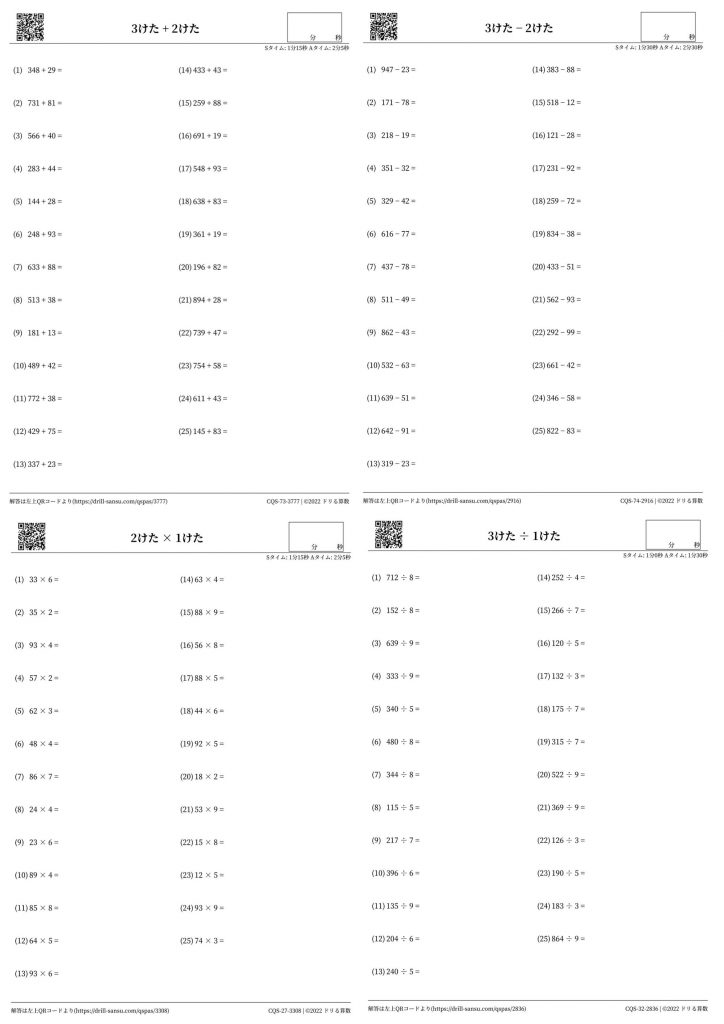
まずは、こちらの計算問題をご覧ください。
※「ドリる算数」に登録すると「プリント学習」 →「 無料プリント」から印刷できます。

こちらの5問をお子様にやってみてもらってください。
できれば、時間を測ってやってみましょう。

さて、いかがでしたでしょうか。

6分以上かかった方は、まだまだのびしろがあります。
4分以内でできた方は、良いですね。基本的な計算力はあります。
理想は2分30秒以内です。

では、計算が苦手なお子様が、この問題を2分30秒以内で解くにはどのように練習していけば良いのでしょうか。
それは、苦手な計算(のびしろ)を見つけ、苦手なところをひとつひとつできるようにしていくことです。

次の計算の答案例をご覧ください。

どうでしょうか。一見、全問正解で、丁寧に解いているように感じるかもしれません。

しかし、「計算くらぶ」で日々、計算問題の答案を添削している私から見ると、改善箇所(のびしろ)がたくさんあります。お分かりでしょうか。

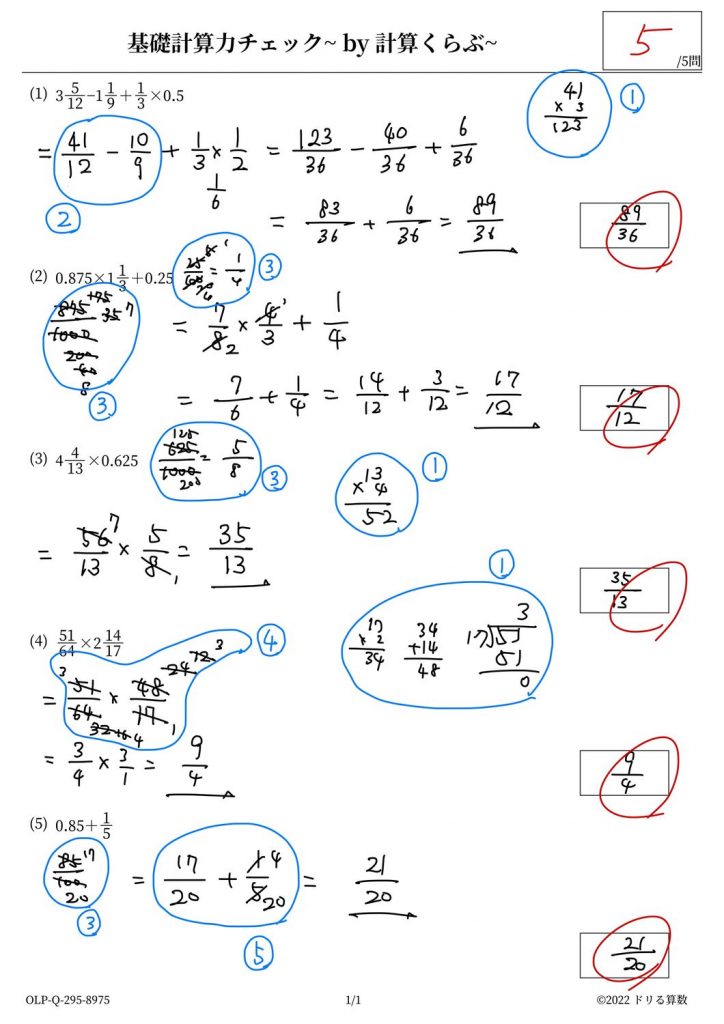
添削したものが以下のようになります。

どうでしょうか。

①〜⑤の番号のそれぞれの改善点を順にお伝えいたします。

 ①簡単な計算は暗算でしよう

まず、「簡単な計算」は暗算で行いましょう。
「丁寧に筆算をした方がミスが減るから筆算をしたい」というお子様もいるのですが、それは間違いです。
書く量が増えると、書き間違いや読み間違いが増えたり、計算スペースを圧迫するからです。
暗算力をつけて、筆算は必要最低限のみで済むようにしましょう。

「簡単な計算」の例
以下の計算を、時間を測ってお子様にやってみてもらってください。

いかがでしたでしょうか。
答えは、

でした。
10秒以内でできなければ、のびしろがあるとお考えください。
暗算でできるような練習が大事になります。「3けた+2けた」,「3けた−2けた」，「2けた×1けた」，「3けた÷1けた」などの計算問題をスピードを意識して練習してください。

 ② 帯分数のたし算・ひき算は、仮分数にしない

次は、帯分数のたし算・引き算の改善ポイントです。
答案例では、(1)の帯分数の計算を以下のように計算しておりましたが、これでは通分が大変です。時間がかかりますし、ミスも誘発します。

なので、次のように、帯分数のまま計算しましょう。
計算が速くなり、ミスも減ります。

 ③ 小数→分数の変換は瞬時にできるように

今度は、小数→分数の変換についてです。
中学受験の計算問題では、小数を分数に変換する作業は頻出です。
そして、よく出る小数は決まっているので、これらを瞬時に変換できるようにしましょう。

よく出る小数を挙げます。お子様に見てもらい、分数に変換できるか聞いてみましょう。

いかがでしたでしょうか。

と瞬時に変換できたでしょうか。

できない場合は、のびしろが大きいです。ぜひ、練習しましょう。

 ④ 約分は一発で

最初の計算で、(4)では約分をこのように解いておりまし

これは、
64と48を
最初に2で割って、32と24
さらに2で割って、16と12
最後に4で割って、4と3

としています。

ここものびしろです。
64と48は、16で割れる！と判断して、一発で割れるようにしましょう。
48と64などの数の最大公約数をパッと言えるように練習することで鍛えることができます。

 ⑤ 小数で計算する方が速いことがある

(5)の計算は、このように解いておりました。

小数と分数が混ざった計算は、とりあえず分数にして計算するお子様が多いですが、ここはのびしろです。

この問題は、

1/5 = 0.2 と、小数に直し、
0.85 + 0.2 = 1.05
と考える方が速いのです。

このように、分数と小数が混ざった計算では、小数に直すのか分数に直すのか判断して計算すると速く・正確に計算ができます。

小数と分数が混ざった計算問題で、とりあえず分数にしないほうがいい例としては、他にも以下の4問があります。
ぜひ、お子様に時間を測って解いてもらってみてください。

解答・解説です。

いかがでしたでしょうか。

理想は10秒で解けるスピードです。

スピードを意識して練習すればすぐにできるようになりますので、ぜひ練習してみてください。

まとめ

ここまで、計算が苦手なお子様に、計算の基礎力を身につけてもらう方法をお伝えしました。

• まずは、計算の答案を添削し、のばすべきところを見つけましょう。ご家庭で添削するのが難しい場合は、お通いの塾や「計算くらぶ」などの計算の添削サービスを利用しましょう。
• 簡単な計算は、暗算で行いましょう。「3けた+2けた」,「3けた−2けた」，「2けた×1けた」，「3けた÷1けた」などの計算問題をスピードを意識して暗算で解く練習をしましょう。
• 帯分数の足し算・引き算は、仮分数にせず、帯分数のまま計算しましょう。
• 小数→分数の変換は瞬時にできるように計算しましょう。
• 約分は、一発でできるように最大公約数をすぐに求められるような練習をしましょう。
• 小数と分数が混ざった計算は、分数で計算するのが速いのか、小数で計算するのが速いのかを判断して計算をするようにしましょう。

のびしろを見つけたら、ひとつひとつ改善し、その後に計算テキストなどで実践練習をしましょう。

また、上記の練習は全て、「ドリる算数」で無料でダウンロードできるようになっております。(2023年6月現在)
下のように、プリント右上に書いてあるSタイムをクリアすることを目標に頑張ってください。
他にも、鍛えるべきものは、「計算力の土台」にまとめておりますので、参考にしてください。

※記事の内容は執筆時点のものです