相似の基礎力｜中学受験算数の基礎力を伸ばす#7

こんにちは。ドリさんです。

突然ですが、お子様は「相似」は得意ですか？

図形問題の中で最重要と言っても過言ではない考え方です。

今回は、相似の中で最もミスをしやすいパターンに絞って、以下の2つをお伝えします。相似が苦手でなぜかいつも間違えてしまうのであれば、この記事でそれが解決するかもしれません。

① 相似の基本的な考え方とピラミッド型

② 相似の問題でミスしやすいのはピラミッド型

①相似の基本的な考え方

まずは、相似の基本的な考え方の図から示します。

以下の問題を考えてみてください。

下の図は、相似な2つの三角形です。□に当てはまる数を求めましょう。
(右の三角形は、左の三角形を同じ形のまま縮小したもの)

すぐに出ましたね。対応する辺の長さを比べて、6cmと2cmが3:1なので、12cmと□cmも同じ3:1の関係であることを利用します。

もしかしたら、12÷3=4と一瞬で求められた方もいるかも知れません。

では、次です。

下の図は、相似な2つの三角形です。□に当てはまる数を求めましょう。

こちらは、どうでしたか。解説です。

今度は、12cmを3で割って2をかける必要があり、少し手順が増えましたが解けましたか。

では、次です。

こちら解答です。

どうでしたか。もしかしたら、以下のように間違えたお子様もいるかも知れませんね。

このような誤答をしてしまうお子様は、相似の基本的なことを忘れてしまい数字に飛びついてしまっています。

そして、よく見るとこの問題は、最初に出題した問題の三角形を重ねた図形です。なので、解き方も全く同じになるのです。(以下の青い三角形と赤い三角形を比べると良いですね)

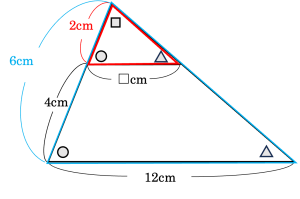
ここまで全問正解で余裕だったお子様は素晴らしいです！
ぜひ、後に載せる問題にチャレンジしてください。

誤答例と同じように間違えたお子様は、チャンスです!
この記事の後の問題を見て、完璧にしましょう。

②相似の問題でミスしやすいのはピラミッド型

相似の問題は、主にクロス型・ピラミッド型とよばれる2パターンあるのですが、ミスをしやすいのは圧倒的にピラミッド型です。なので、この記事ではピラミッド型のみ扱います。下の4パターンを解いてみてください。

それでは解説です。

いかがでしたでしょうか。

(1)~(3)がわからないお子様は、形の同じ三角形2つを色分けして見比べてみてください。ミスに気づくはずです。

また、(4)は特にミスしやすいです。なぜかというと、多くのお子様は、答えが整数になってほしいと無意識に願っているからです。答えが分数や小数になると無意識に間違えていると思い込んでしまいます。

この4問を完璧に解けた方は、相似が得意だと胸を張ってください。間違えてしまった人は、ドリる算数の相似(ピラミッド型)で、トレーニングしましょう。現在、無料でできます！（2023年7月時点）

まとめ

「相似の基礎力」に関しては、次の2つのポイントを説明しました。

① 相似の基本的な考え方とピラミッド型

② 相似の問題でミスしやすいのはピラミッド型

1つめは、相似の基本的な考え方を説明しました。相似ってそもそもなんだっけ?ということを説明しました。相似がわからなくなったら思い出しください。

2つめは、相似の問題でミスのしやすいのは、ピラミッド型だということでした。特にその中でもミスのしやすい4パターンをまとめましたので、相似の問題に引っかかった時に、ぜひ、ご確認ください。

以上です。

相似の問題が得意になりますように！

※記事の内容は執筆時点のものです