「場合の数」が苦手になりやすいのはなぜ? 順列や組合せの問題で正解できない理由5選
中学受験算数の「場合の数」は、多くの受験生が苦手とする単元です。特殊算や図形などが得意でも、場合の数の問題ではなかなか正解できない受験生も少なくありません。今回は、場合の数が苦手になりやすい理由と、それを解決するための方法を紹介します。
Contents [hide]
場合の数は高校数学の先取り
中学受験生が場合の数を苦手とする場合、その原因は勉強不足や能力不足ではありません。そもそも中学受験算数の場合の数は、高校数学の場合の数とほとんど同じです。高校生ですら苦手とすることが多い分野ですから、難しいのは当たり前といえます。中学受験生は、苦手だからといって悲観するのではなく、前向きに取り組むとよいでしょう。
場合の数が苦手になりやすい理由5選
場合の数が苦手になりやすい理由とその解決方法を、具体的な問題を通して解説します。
1. 問題文を正しく理解できない
【問題1】男子5人、女子4人の中から3人の選手を選ぶとき、少なくとも1人は女子である選び方は何通りありますか。
【問題1】の「少なくとも1人」は1人、2人、3人の場合があります。それぞれの場合の数を求めるよりも、すべての場合の数を求めた後に、女子が1人もいない場合の数=3人の選手が全員男子の場合の数を引くのが楽です。
- すべての場合の数は(9×8×7)÷(3×2×1)=84(通り)
- 3人の選手が全員男子の場合の数は(5×4×3)÷(3×2×1)=10(通り)
- 求める場合の数は84-10=74(通り)
「少なくとも1人」を「1人」と誤解してしまうように、問題文を正しく理解できないと不正解になります。
問題文を正しく理解するための対策としては、場合の数に特有の言い回しを覚えてしまうとよいでしょう。
2. 公式を使って解けるとは限らない
【問題2】1,1,2,3,4の数字が書かれた6枚のカードの中から2枚を取り出すとき、取り出し方は何通りありますか。
高校数学の組合せの公式Cを塾で教わった受験生も少なくないでしょう。しかし、異なるものの中から選ぶ場合に使えるCは、1のカードが2枚ある【問題2】では使えません。下の図のように樹形図を描いて7通りを求めるのが楽です。

【問題2】のように、公式を使っても解けない問題が多いのが場合の数です。意味を理解していない公式を使わず、樹形図などで地道に数え上げましょう。
公式Cについては、次の記事でくわしく解説しています。
3. 数え上げるときに抜け漏れや重複が出やすい
【問題3】黒い碁石3個、白い碁石2個を横1列に並べるとき、並べ方は何通りですか。
【問題3】では、すべての場合を書き出して数え上げる解き方が考えられます。このとき、一部の場合を書き忘れたり、同じ場合を書いたりすると、正しい答えを求められません。こうした抜け漏れや重複を防ぐには、自分なりにルールを決めて規則正しく書くことが大切です。
【問題3】では、下の図のように書き出して10通りを求めました。白い碁石を赤と青の矢印で示した通り、規則正しく移動させることがポイントです。

4. 似たような問題の違いがわかりにくい
【問題4】以下の硬貨を使って支払える金額はそれぞれ何通りですか。
(1) 100円玉1枚、50円玉1枚、10円玉3枚
(2) 100円玉1枚、50円玉3枚、10円玉1枚
【問題4】の(1)と(2)は似たような問題ですが解き方が違います。
(1)は10円玉5枚で50円にしたり、50円玉2枚で100円にしたりできません。そのため、それぞれの硬貨の枚数だけを考えれば問題ありません。
- 100円玉の使い方は0~1枚の2通り
- 50円玉の使い方は0~1枚の2通り
- 10円玉の使い方は0~3枚の4通り
- 0円の1通りを引いて、2×2×4-1=15(通り)
一方、(2)は50円玉2枚で100円になります。このような場合、大きい金額の硬貨を小さい金額に両替します。(2)では、100円玉1枚を50円玉2枚に両替して50円玉5枚と考えて、次のように計算します。
- 50円玉の使い方は0~5枚の6通り
- 10円玉の使い方は0~1枚の2通り
- 0円の1通りを引いて、6×2-1=11(通り)
【問題4】のような問題に引っかからないためにも、似たような問題の「どこが違うのか?」を比べて言語化する習慣を身に付けましょう。
5. 同じタイプの問題に気づきにくい
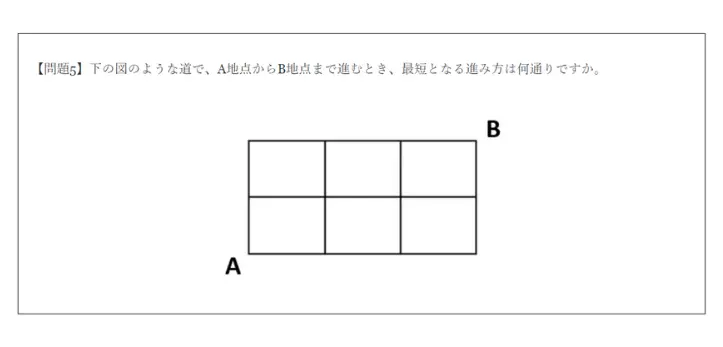
【問題5】下の図のような道で、A地点からB地点まで進むとき、最短となる進み方は何通りですか。

【問題5】は、「最短となる道順」なので、右→か上↑に進むことしかできません。そのため、下の図のように、十字路・丁字路・曲がり角に進み方の和を書き込んでいけば、10通りが答えだとわかります。

しかし、【問題5】は右→3個、上↑2個の並べ方を考えれば解ける問題でもあります。→→↑→↑や↑→→↑→などの並べ方がありますが、これは【問題3】と同じ考え方です。したがって、【問題3】と同じ図を描いても10通りを求められます。
全く異なる問題に見える【問題3】と【問題5】ですが、実は同じタイプの問題です。このような問題に出会ったら、「どうして同じように解けるのかな?」を考えて言語化することで、算数の力が大きく伸びるはずです。
場合の数の勉強で思考力を鍛える
場合の数は、計算することよりも考え方が大切なので、思考力を鍛えるのにぴったりな分野です。苦手意識から避けるのではなく、「どうしてそうなるのか?」を考え抜くことで、勉強して得たものが中高の数学にもつながります。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます




