帯分数の計算を効率よく！ピザでイメージしてみよう｜中学受験算数きほんの「き」！#6

こんにちは！中学受験算数のオンライン個別指導講師　さちです。

「計算くらぶ」にて中学受験算数の計算添削も行っています。

今回の記事のテーマは「帯分数の計算」です！

中学受験塾では4年生で学ぶ内容ですが、実は5，6年生でも分数の計算に穴がある子が多いです。

• 教わったやり方を覚えてその通りにやってるよ
• いつも正解できているから大丈夫！

という子でも、やり方を間違えて覚えていたり、非効率なやり方になっていることも多いです。

この記事では、図を用いて「帯分数の計算」の考え方を解説していきます。

分数の計算が苦手な方はもちろん、「自分は大丈夫」と思っている方もぜひ読んでみてください！

ピザ3/4枚とピザ3/4枚を合わせると何枚になる？（帯分数のたし算）

それではさっそく帯分数のたし算をやってみましょう！

問題.ピザ3/4とピザ3/4を合わせると何枚になるでしょうか？

図にしたのがこちらです↓

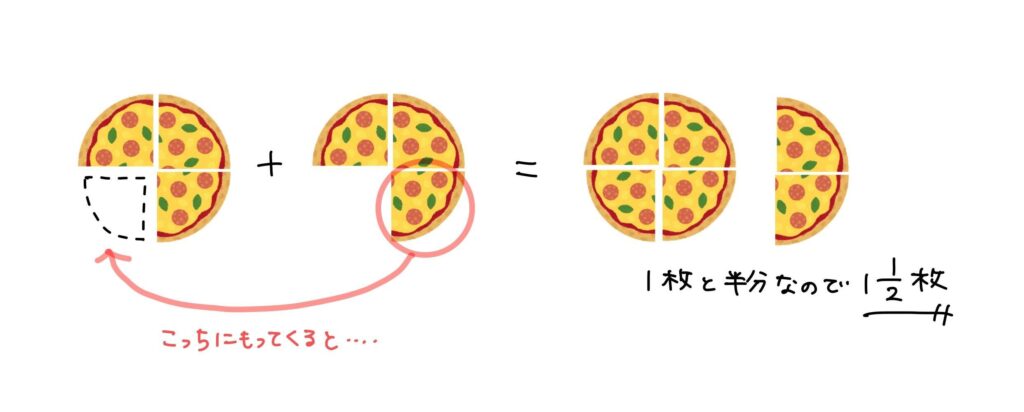
計算式で考えると以下のようになります。

計算式をすべて頭の中で考えるのはなかなか難しいですが、図をイメージすると暗算でもできそうですね。

帯分数のひき算

続いて、ひき算です！

問題.ピザが2枚ありました。そのうち1/4枚を食べると何枚になりますか？

図であらわすとこのようになります。

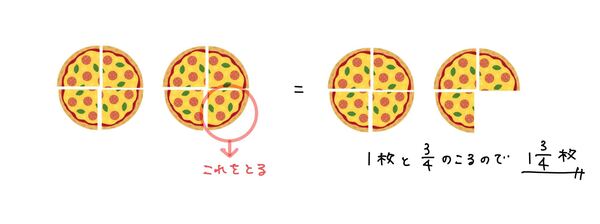
計算式で書くと以下のようになります。

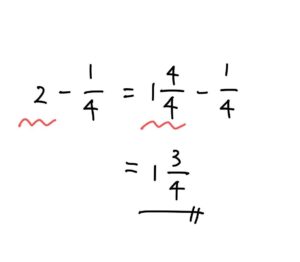
2を1と4/4にする部分が分かりづらいと感じる子も多いですが、上のように図を書くとイメージがしやすくなりますよ。

帯分数のかけ算

次は

をやってみましょう！

ほとんどの受験生は解き方を1通りしか知りません。

しかし、実はピザをイメージすると簡単に解ける別の解き方もあります。

解説を読む前にぜひ考えてみてください！

まずは多くの受験生が思いつく方法を紹介します。

帯分数のかけ算の基本である「帯分数を仮分数に直す」に忠実に計算すると、以下のようになります。

一方、図で考えると以下のようになります。

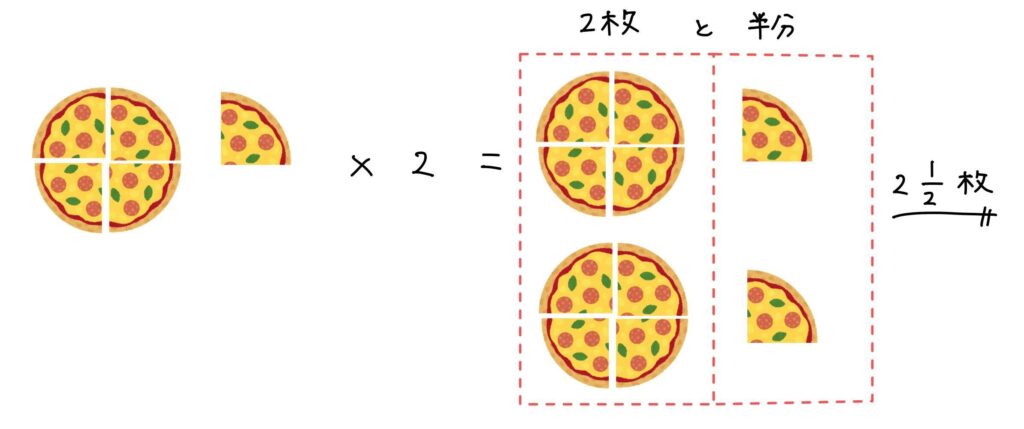
これだと暗算でもできますね。

基本に忠実な方法も大切ですが、こちらの考え方でもできるようにしておくと役に立ちますよ。

帯分数のわり算

最後はわり算です！

をやってみましょう！

こちらも、2通りの解き方で説明します。

そしてこちらもピザをイメージすると一瞬で解ける方法があるので、ぜひ考えてみてください！

それでは解説です。

帯分数のわり算の手順に忠実に計算すると、以下のようになります。

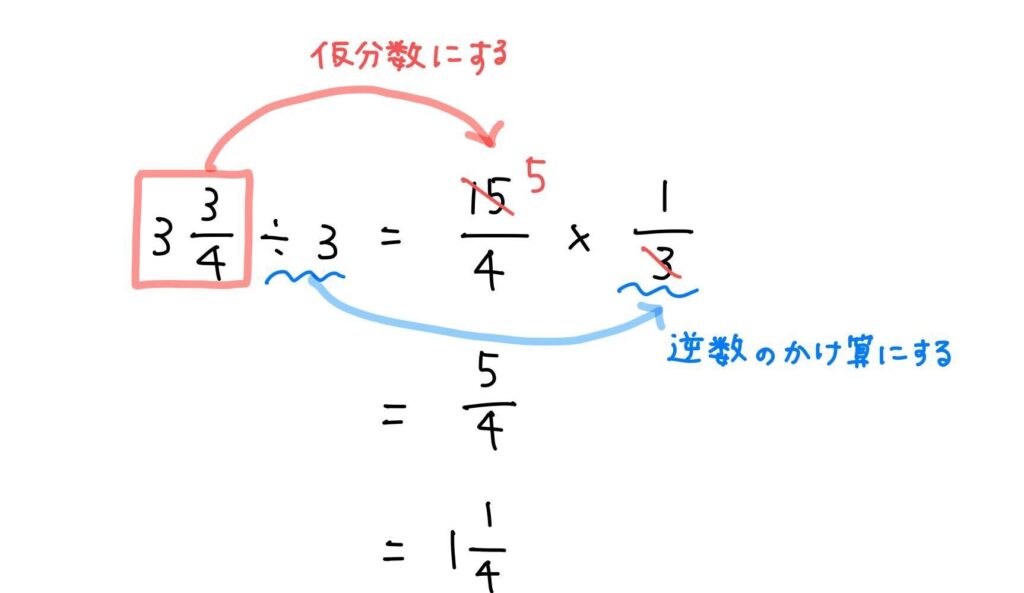
次に、図で表してみました。

分数のわり算のやり方を習っていなくてもできてしまいますね。

まとめ

この記事では「分数の計算をイメージしながらやる」方法を紹介しました。

図をイメージすることで、計算式を書かなくても自然と答えが思い浮かぶ場合があることを知っていただけたかと思います。

計算の手順を覚えることは大切ですし、必要です。

ただ、かえって時間や手間がかかり、計算ミスをにつながってしまうこともあります。

• 手順に従って計算する
• 図を思い浮かべて考える

という方法を状況に応じて使い分けられるといいですね。

※記事の内容は執筆時点のものです