てこの原理とは？ 計算方法や、問題を解くための「王道アプローチ」を紹介

中学受験理科の物理分野で登場する、てこの原理。難しそうなイメージのある単元ですが、「回転しようとする力（＝力のモーメント）」の計算を確実におこない、「つりあいの式」を正しく立てることで攻略できます。この記事では、てこの原理の基本となる「回転しようとする力」の計算方法を解説するだけでなく、実際に問題を解くために知っておきたい「王道アプローチ」、そして簡単な例題をもとに基礎知識も確認していくので、てこの原理に苦手意識を持っている子はぜひ読んでみてください。

「てこの原理」とは

そもそも「てこの原理」とは、物理の原理のひとつ。「小さな力で大きな力を生み出すことができる原理」のことを指します。ただし、これだけだと少しイメージしづらいかと思うので、まずは公園にあるシーソーをイメージしてみましょう。

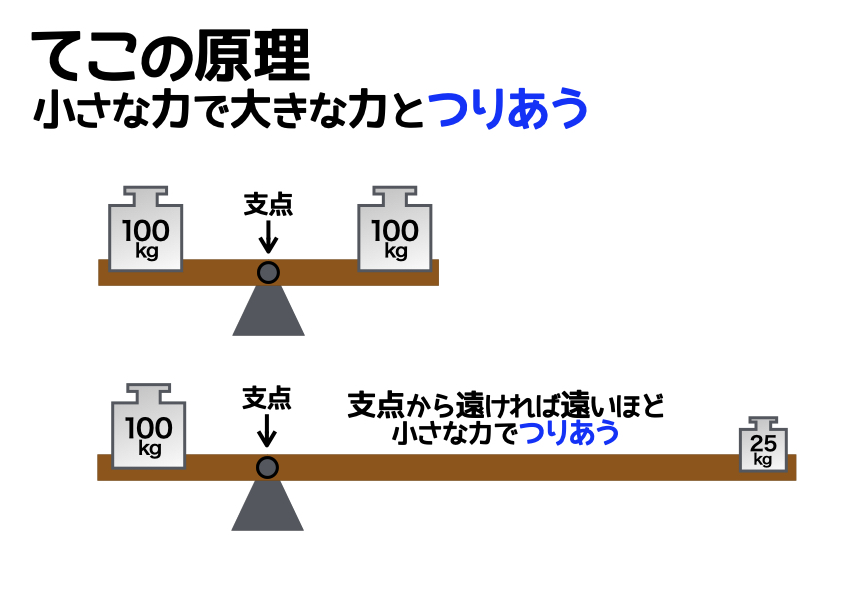片方に100kgのおもりが乗ったシーソーを思い浮かべてみてください。この場合、まずは支点を中心として左右が同じ長さのシーソーであれば、もう片方に100kgのおもりを乗せると「つりあった状態」になります。

一方で、おもりを乗せる位置を支点から遠く離れた場所にすると、25kgといった小さなおもりでも「つりあった状態」にすることができてしまいます。

では、どうして小さなおもりでもつりあうのでしょうか？ それはシーソーにおもりを乗せることによって起こる力、つまり「回転しようとする力」が支点を中心に発生することに関係しています。この力は「モーメント」と呼ばれ、簡単に計算できます。

「回転しようとする力」を計算しよう

「回転しようとする力（モーメント）」は、シンプルなかけ算で計算可能です。

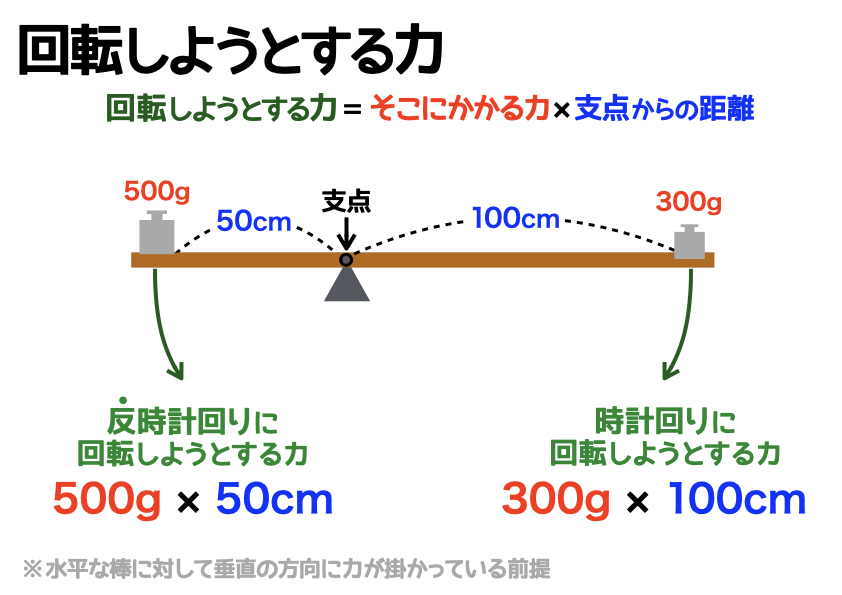まず、左に置かれた500gのおもりに注目してください。このおもりは支点から50cm離れた場所に乗っているので、「500g×50cm」と計算できます。右の300gのおもりも同様に、「300g×100cm」と計算します。

ここで大切なのが、回転しようとする力の“方向”を考えることです。上の図を見ると、500gのおもりは「反時計回り」に回転しようとする力、そして300gのおもりは「時計回り」に回転しようとする力がかかっていますね。そしてそれぞれを計算すると、反時計回りに回転しようとする力（500g×50cm）のほうが大きいことがわかります。

3種類の「てこ」

「てこの原理」の基本を、シーソーをイメージしながら紹介してきました。しかし実は、てこには大きく分けると3種類のパターンが存在します。

では、「誰かから100kgのモノを持ち上げてほしい！」というお願いをされた場合を想定して、それぞれのパターンを使った解決方法を見ていきましょう。

［1］シーソー型

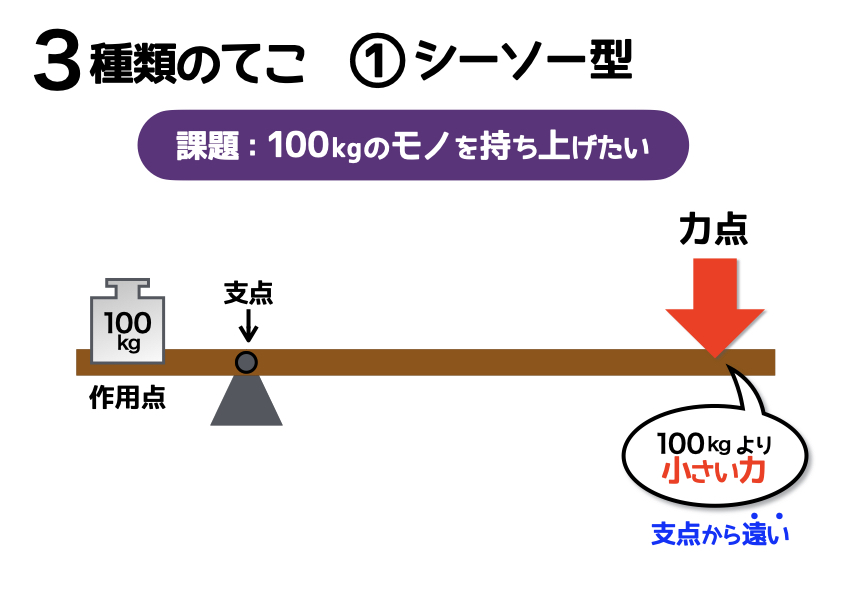ひとつ目は、ここまで紹介してきた「シーソー型」です。シーソー型の場合、支点から遠く離れた場所におもりを置けば置くほど、100kgよりも小さな力でおもりを持ち上げることができます。

［2］せんぬき型

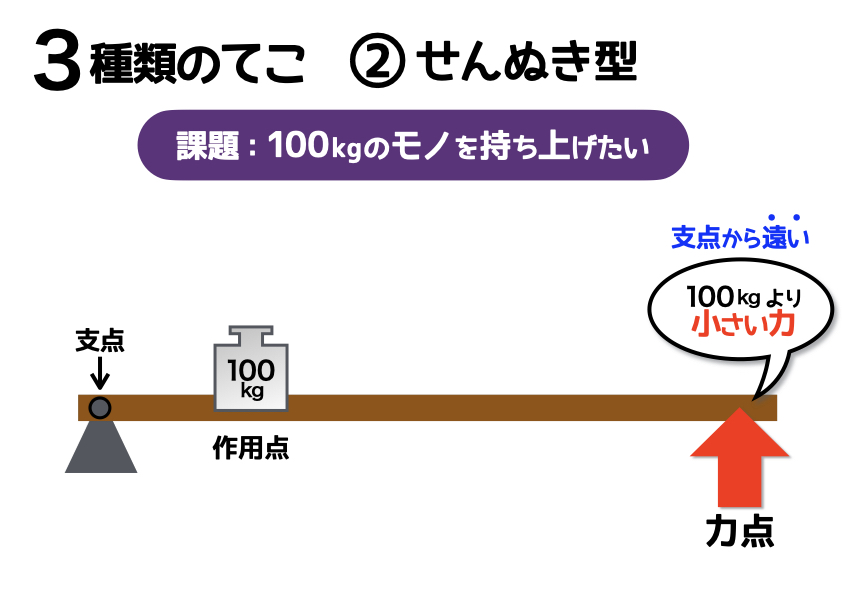
ふたつ目は「せんぬき型」です。上の図を見ると、シーソー型と違い、力点も作用点も同じ側、つまり「支点の右側」にありますね。でも、考え方はシーソー型と同じ。まずは、支点からの距離に着目します。この場合には、支点から遠く離れた場所に下からの力が加わるほど、100kgよりも小さな力でおもりを持ち上げることができます。

［3］ホッチキス型

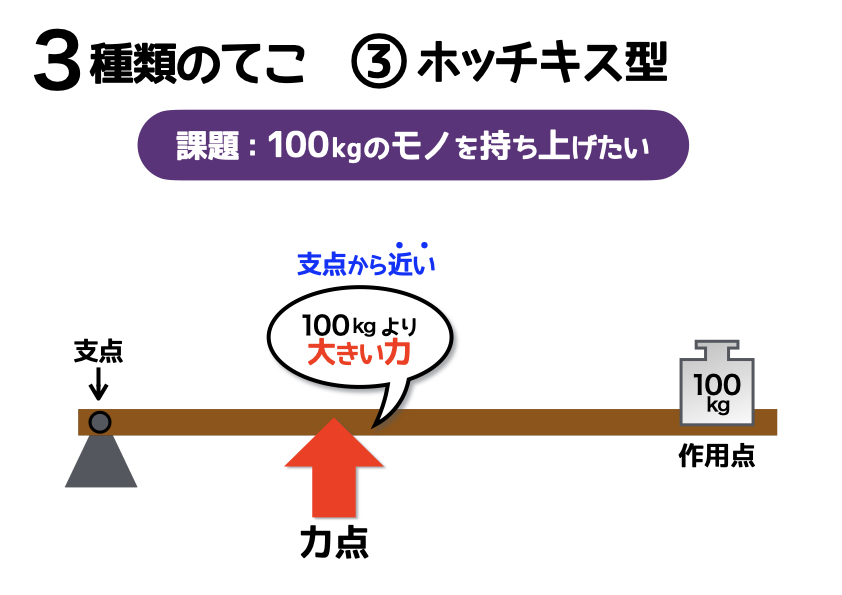
最後は「ホッチキス型」です。一見するとせんぬき型と似ていますが、ホッチキス型の場合には力点が支点に近い場所にあります。この場合、100kgのおもりを持ち上げるためには、下側から100kgより“大きな力”が必要となります。

シーソー型も、せんぬき型も、100kgより“小さな力”で持ち上げることができました。一方でホッチキス型の場合には、100kgよりも重い力が必要になってしまいます。ではホッチキス型のてこは、いったい何の目的で使われるのでしょうか？ それは、たくさんのモノを移動させたいときです。たとえば上の図の場合、100kgよりも大きな力が必要な代わりに、たとえば作用点のおもりを1cm動かしただけで、力点のおもりも1cm以上移動させることができるとされています。

力学問題の「王道アプローチ」

次は、力学の問題が出てきたときに意識したい「王道的なアプローチ」を紹介します。