
比を利用する問題の基礎力|中学受験算数の基礎力を伸ばす#8
こんにちは。ドリさんです。
突然ですが、お子様は「比」は得意ですか?
中学受験で文章題から図形まで、いろんな分野に比は利用されます。比の操作に慣れておくことで、いろんな場面で応用が効きますので、この記事で基本的な操作を確認しておきましょう。
今回は、比を利用する問題の中で、よく出る「倍数変化算」という問題を解くことを目標にして、以下の3点の順で基礎から確認していきます。
① 基本的な比の使い方
② マルイチ算の計算
③ 倍数変化算の問題を解く
Contents [hide]
①基本的な比の使い方
まずは、基本的な比の使い方を使いましょう。
まずは、以下の問題を2通りの解き方で確認しておきましょう。
比を習っていれば解けると思いますが、お子様がどういう風に解いてるか確認してみてください。
5:2 = □:6
では、2通りの解き方で解説をします。
解き方1 ・・・マルイチ(比の1あたりの量)を求める
※ ①,②などは,比を表すと考えてください。例えば、③=12なら、①=12÷ 3 =4 となります。
5:2 = □:6
② = 6
① = 3
⑤ = 15
解き方2 ・・・比例式の性質を使う
比例式の性質を使う解き方です。
内向の積 = 外側の積 (A:B=C:D のとき、 B×C = A×D となる。)
5:2 = □:6
2×□ = 5×6 ※ 内側のかけ算と外側のかけ算は同じ。
2×□ = 30
□ = 30÷2 = 15
いかがでしょうか。
どちらで習ったとしても、どちら解き方もできるようにしておきましょう。 この問題の練習プリントに関しては、「ドリる算数」の「計算力の土台の比」で無料でダウンロードできるようになっております。(2023年8月現在)

②マルイチ算の計算
次は、マルイチ算の計算です。倍数変化算を解くときによく出てくる計算なのですが、練習する機会があまり多くありません。方程式のように移項(=の反対側に、+□であれば-□にして移動させること)して解きがちなのですが、移項を知らないお子様からすると意味がわかりづらいです。
線分図を書いて解いてみましょう。
3問用意してみました。
解けることも大事ですが、それ以上に線分図を書けるかどうかお子様に解いていただき、確認してみましょう。
※ ①,②などは,比を表すと考えてください。例えば、③=12なら、①=12÷ 3 =4 となります。
Q. ①の値を求めましょう。
1. ⑦ + 3 = ③ + 15
2. ② + 7 = ⑨ – 14
3. ⑤ – 12 = ② – 3
いかがでしたでしょうか。
正しい線分図と解答は、こちらです。
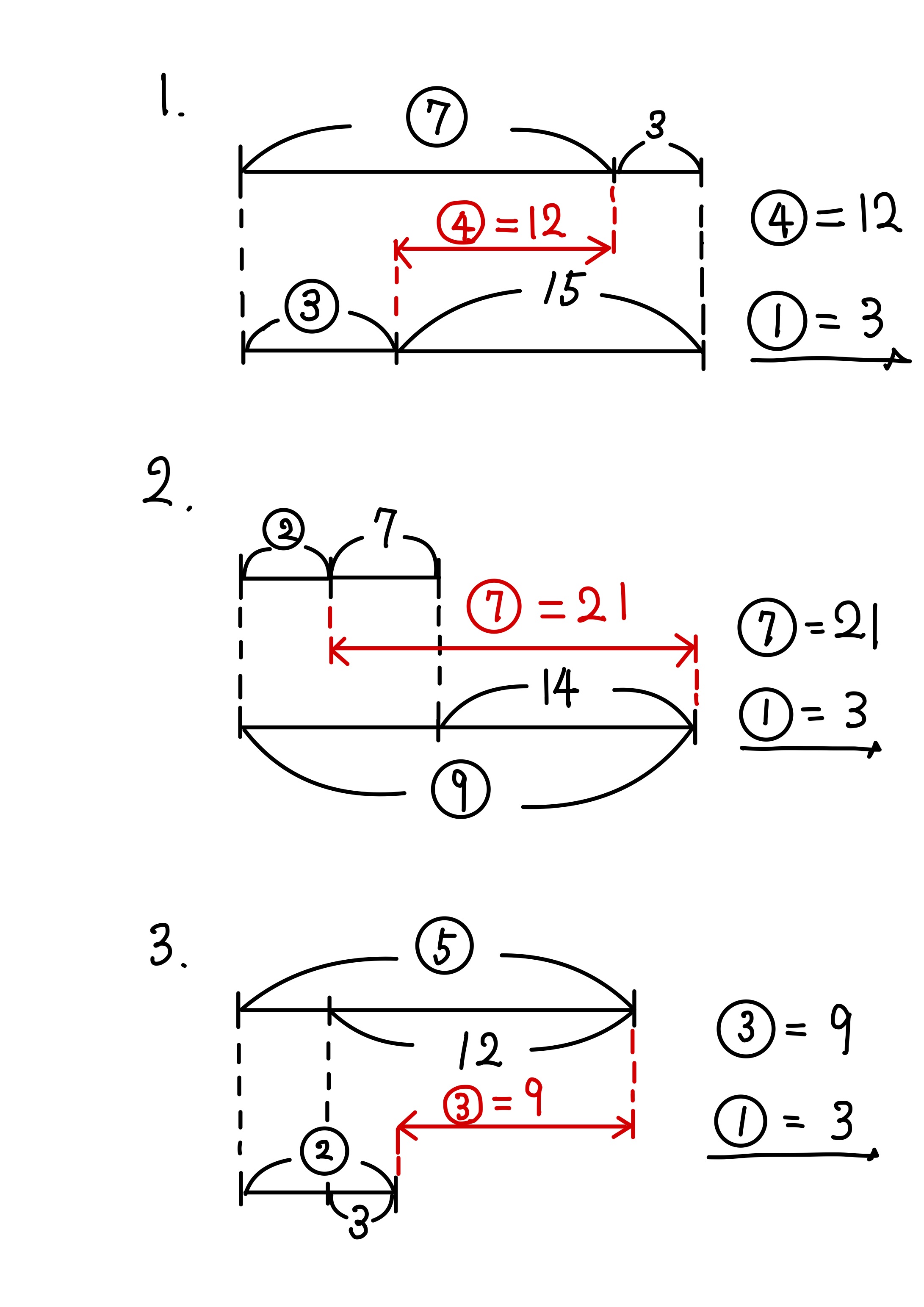
いかがでしたでしょうか。慣れないうちは線分図を書くのも大変ですが、だんだんと慣れてきます。さらに、練習を積み重ねると線分図を書かずに解けるようになります。
この問題を練習するには、「ドリる算数」の「マルイチを求める」で無料でダウンロードできるようになっております。(2023年8月現在)

③ 倍数変化算の問題を解く
さて、最後は倍数変化算と呼ばれる問題を解きます。
では問題です。
こちらの問題をお子様に考えてみてもらいましょう。
はじめ、兄と弟の所持金の比は、2:1でしたが、兄は1200円を使い、弟は600円を父からもらったので、
兄と弟の所持金の比は、2:3となりました。はじめの兄の所持金はいくらでしたか。
いかがでしょうか。
どこから解いていいか解らないお子様のために、少しヒントをお伝えします。
はじめの兄: ②
はじめの弟: ① とすると、
②-1200:①+600 = 2:3
いかがでしょうか。ここまでの式は理解しやすいかと思います。
実は、ここまでくれば、あとは計算だけです。
「比例式の性質を使う解き方」を応用しましょう。
続きです。
②-1200:①+600 = 2:3
(①+600)×2 = (②-1200)×3 ※ 内側のかけ算と外側のかけ算は同じになる。
①×2+600×2 = ②×3-1200×3
②+1200 = ⑥-3600
ここまできたら、あとは線分図を書いて解くだけです。
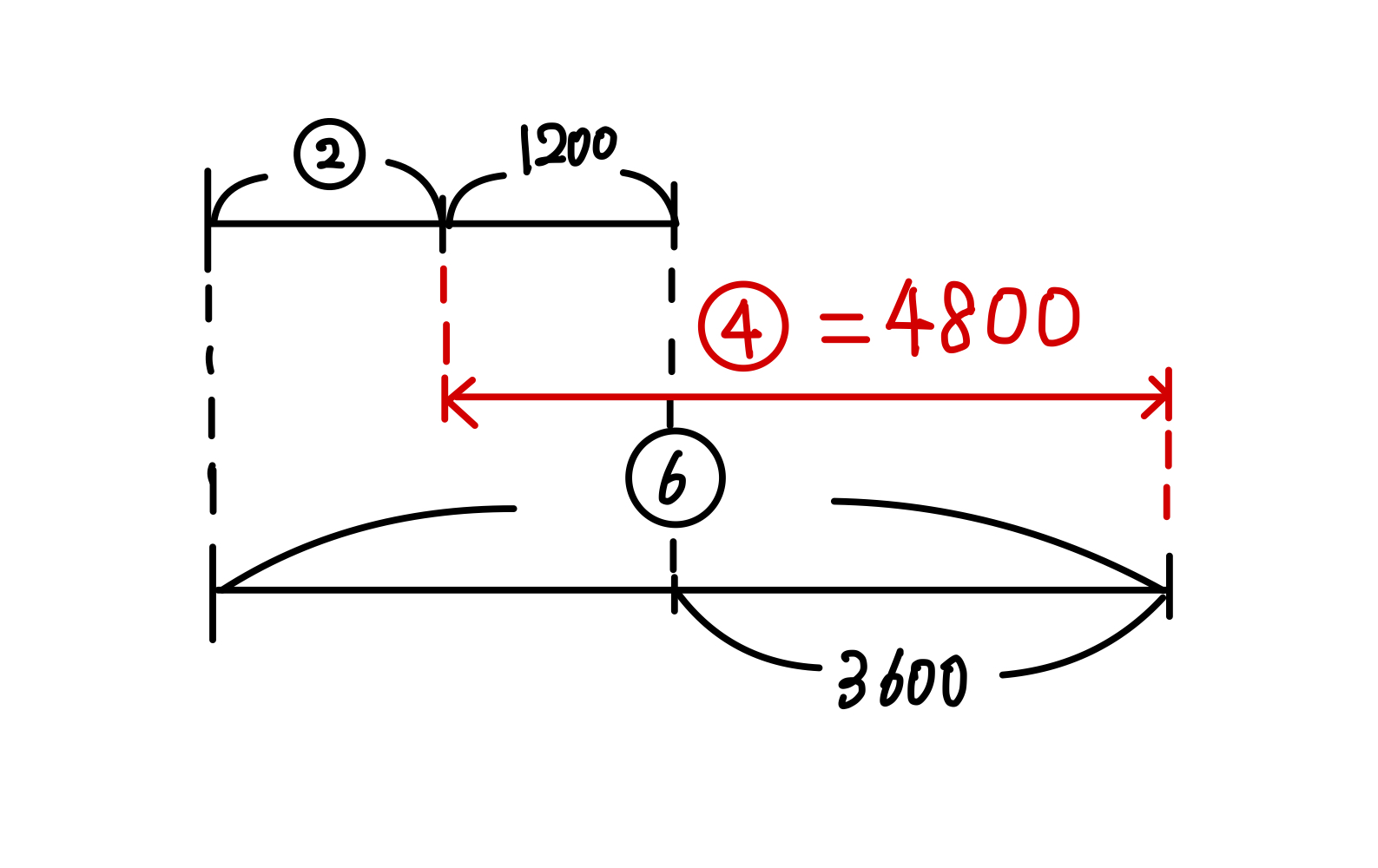
④ = 4800
① = 1200
はじめの兄・・・② = 2400円
以上で解けました!
比例式の性質を使うところ、線分図で処理をするところさえしっかりと鍛えられていれば簡単に解けます。
まとめ
倍数変化算を解くまでのステップを説明しました。
① まずは、基本的な比の使い方に慣れましょう。1あたりの値を出して解く方法(マルイチを求める)と、比例式の性質を使って解く方法の両方を知っておくことが大事です。
② マルイチ算の計算は、方程式のような移行を使って解く考え方ではなく、線分図を書いて解きましょう。練習をしていると慣れてきます。
③ 倍数変化算の問題を解くには、比例式の性質とマルイチ算の解き方を使います。
以上です!
比やマルイチ算の処理ができるようになると、色々な場面で応用ができますので、ぜひ練習をしてみてくださいね。
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

