【小6理科／てこと力のつりあい】支点を決めて、てこの計算を攻略しよう｜中学受験のツボ［理科編］

国語｜算数｜社会

今回のテーマは「てこの計算」です。

単純な「てこ」だと答えられても、おもりやバネばかりなどがゴチャゴチャついてくると、混乱してしまうお子さんが多いです。

でも、一見すると複雑そうな計算問題も、考え方を変えれば解決できるんです。その方法を、一緒に見ていきましょう。

モーメントを理解しよう

まず、てこの問題を考えるうえで重要な考え方は、「モーメント」というものです。

「棒を回転させる働き」とも言います。

これは「支点からの距離×重さ」で決まってきます。

支点からの距離や重さは目に見える具体的な量ですが、モーメントは架空の数字なので、慣れるまでは少し厄介かもしれません。

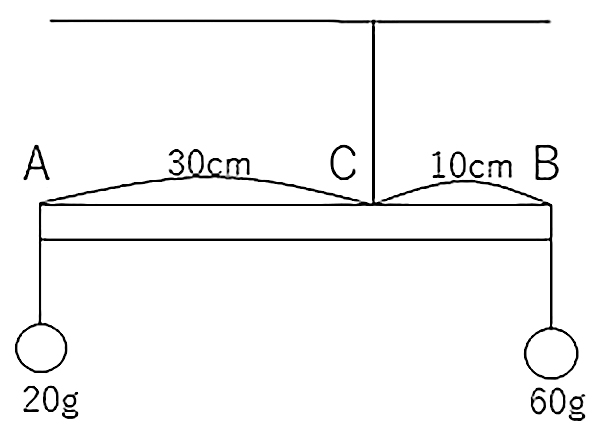
モーメントを理解するために、次の【図1】のてこのつりあいを考えてみましょう。棒や糸の重さは無視できるとします。

【図1】

てこの問題を解くうえで重要なことは「支点を決めること」です。

支点が定まらないと、支点からの距離が求められないので、まず最初に支点を決めます。

この図をもとに、お子さんに「支点はどこ？」と聞いてみましょう。

おそらく、ほとんどのお子さんが「天井と棒をつなぐ点C」と答えると思います。

その答え自体は間違ってはいません。