【小6算数／規則性】あみだくじを繰り返し使う問題の考え方｜中学受験のツボ［算数編］
こんにちは。
株式会社ORA-Trio杉本です。
今回のテーマは「あみだくじ」です。
あみだくじで、選んだ点がどこに移動するか、それを繰り返すとどのような結果になるか、といった問題です。
このような問題のコツは、「移動する点すべて」ではなく「一つひとつの動き」に注目すること。一つひとつの点の移動に注目することで「規則性」の問題ととらえることができます。
今回は、あみだくじの問題のポイント、「規則性」の問題としてとらえるコツについてお話しします。
「あみだくじを繰り返す」問題の基本的な考え方
まずは、あみだくじの基本的な動き、そして「あみだくじを繰り返す」とはどういうことかを確認してみましょう。
以下の例題を見てください。
例題
図1のようなあみだくじを使って、A君、B君、C君、D君、E君の場所を入れ替えます。A君は点ア、B君は点イ、C君は点ウ、D君は点エ、E君は点オからスタートし、曲がり角があれば必ず曲がって進みます。
（1）このあみだくじを通ると、5人はどのような並び順になりますか。
（2）このあみだくじを2個つなげて図2のようなあみだくじをつくります。このあみだくじを通ると、5人はどのような並び順になりますか。
（3）このあみだくじを何個つなげると、5人が最初と同じ並び順になるあみだくじになりますか。考えられる最も少ない数を答えなさい。
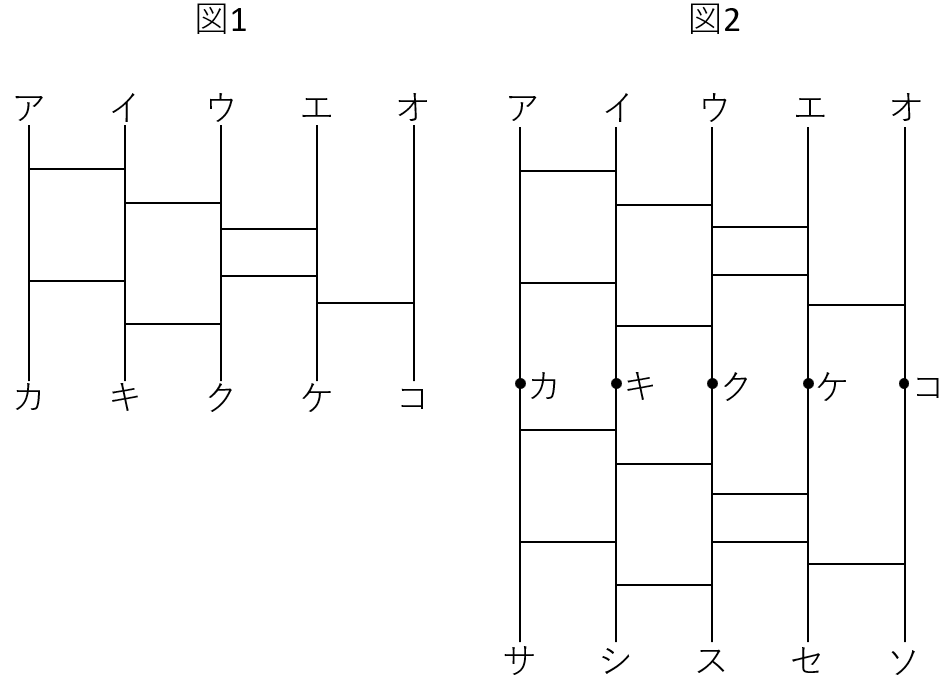
（1）は、一つひとつ確認するだけですね。
たとえば、A君の動きは下の図のようになります。
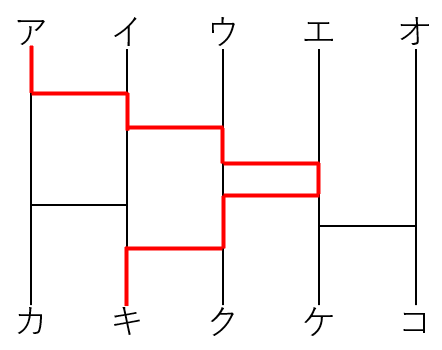
つまり、A君は点キにたどり着くということですね。
同じように考えると、B君は点ク、C君は点カ、D君は点コ、E君は点ケに、それぞれたどりつきます。
よって、答えは「C、A、B、E、D」となります。
次に（2）についても、一人ひとりの動きについて考えてみましょう。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます