学習 算数

正多角形にはどのような性質がある？ 入試によく出る図形問題を解くコツを紹介

2024年5月09日 みみずく
LINEで送る

ポスト

このエントリーをはてなブックマークに追加

0

　　

中学入試算数の図形問題でよく出るのが正多角形です。特に正五角形以上になると、苦手とする中学受験生も少なくありません。そんな正多角形の基本的な性質を理解し、典型問題のパターンを覚えましょう。

正多角形の基本的な性質

正多角形の基本的な性質を覚えれば、内角と外角の大きさを求められます。

正多角形とはどんな図形か？

正多角形とは、全ての辺の長さが等しく、全ての内角（隣り合った2辺が多角形の内側に作る角）の大きさが等しい多角形です。正三角形、正四角形（正方形）、正五角形、正六角形が入試問題によく出ます。

正多角形は全て線対称です。線対称な図形は、1本の直線（対称の軸）で折り返すと両側がピッタリ重なります。また、正N角形の対称の軸はN本です。その理由は以下の通りです。

  • Nが奇数のとき、対称の軸は各頂点と対辺（向かい合う辺）の中点（真ん中の点）を結んだ直線が対称の軸になる。したがって、対称の軸の本数＝頂点の数＝N。
  • Nが偶数のとき、向かい合う2つの頂点を結んだ線と、向かい合う辺の中点を結んだ線が対象の軸となる。したがって、対称の軸の本数＝（頂点の数）÷2＋（辺の数）÷2＝N。

一方、正N角形のうち、Nが偶数のときは点対称にもなります。点対称な図形は、1つの点（対象の中心）を中心として180°回転させたときにピッタリ重なります。

正多角形の内角と外角の大きさの求め方

正N角形の1つの内角と1つの外角の大きさをそれぞれ求めましょう。外角とは、1辺を延長した直線と、これに隣り合う辺が作る角です。

N角形の内角の和と外角の和は次の通りです。

  • N角形の内角の和＝180°×（N－2）
  • N角形の外角の和＝360°

正N角形は全ての内角の大きさが等しいので、180°から内角の大きさを引いた外角の大きさも全て等しくなります。したがって、次のことが成り立ちます。

  • 正N角形の1つの内角の大きさ＝180°×（N－2）÷N
  • 正N角形の1つの外角の大きさ＝360°÷N

たとえば、正10角形の1つの内角の大きさは180×（10－2）÷10＝144°、1つの外角の大きさは360÷10＝36°です。

正多角形の問題の解き方

正多角形の問題の中から、正五角形と正六角形の問題を紹介します。

正五角形と平行線の問題

【問題1】下の図の五角形ABCDEは正五角形で、直線mと直線nは平行です。このとき、角アの大きさを求めなさい。

解き方はいろいろ考えられますが、下の図のように、辺DEをEの方に延長して補助線を引き、直線mとの交点をFとして、角イの大きさを求めるのが楽でしょう。角アと角イは平行線の錯角なので、大きさは等しくなります。

まず、三角形EFGに注目して、角FEGは正五角形の外角なので、その大きさは360÷5＝72°です。

次に、正五角形ABCDEの1つの内角の大きさは180×（5－2）÷5＝108°です。角BAG＝角ABC＝108°とわかり、角ABG＝108－88＝20°とわかりました。また、三角形ABGの内角と外角の関係から角AGF＝角BAG＋角ABG＝108＋20＝128°です。

最後に、三角形EFGの内角と外角の関係から、角イ＝角AGF－角FEG＝128－72＝56°と求められました。したがって、角ア＝角イ＝56°が答えです。

平行線と正多角形の融合問題では、他にも正方形や正六角形がよく出ます。考え方は同じなので、どこに補助線を引くかを覚えておくとよいでしょう。

正六角形の内部にある三角形の面積

【問題2】下の図のように、面積が72cm\(^2\)の正六角形の内部に三角形を作りました。色のついた部分の面積を求めなさい。

52481

正六角形の性質として、対辺（向かい合う辺）同士は平行です。そのため、下の図のように、内部の三角形の頂点のうち、正六角形の辺上にある頂点を移動することができます。底辺が共通で高さが等しい三角形は面積が同じになることを利用した等積変形を行いました。さらに、右の図のように、正六角形の頂点同士を結んで6等分し、面積の等しい三角形を6つ作りました。

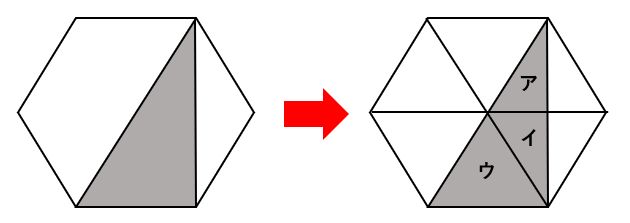
色のついた部分の面積は（三角形ア＋三角形イ＋三角形ウ）の面積です。三角形アと三角形イは合同な三角形なので、（三角形アと三角形イ）の面積は三角形ウの面積と等しいことがわかります。したがって、（三角形ア＋三角形イ＋三角形ウ）の面積は、正六角形を6等分してできた三角形2つ分の面積と等しいといえます。これより、色のついた部分の面積は72÷6×2＝24cm\(^2\)です。

正六角形を題材とした面積の問題では、正六角形を分割して面積の等しい三角形を作っていくことが大切です。どのように分割すればよいかは過去記事で確認してください。

正多角形から図形問題のコツを学ぶ

正多角形の問題は、同じ長さの辺や同じ大きさの角を見つけたり、同じ形の図形に切り分けたりすることが求められます。これらの作業は全ての図形問題に通じる考え方です。そのため、正多角形の問題を解くことは図形問題のコツを学ぶのに役立ちます。苦手意識を持たずに取り組んでみることが大切です。

※記事の内容は執筆時点のものです

0

とじる

お気に入り機能は
会員の方のみご利用できます

会員登録のうえログインすると
お気に入り保存できるようになります。

お気に入りのコンテンツは、
マイページから確認できます

＼ 初めての方はこちら ／

会員登録

＼ ご登録済の方はこちら ／

中学受験ナビ会員になると