
【小5算数/立体図形】立体切断による「変化」に注目しよう|中学受験のツボ[算数編]
こんにちは、杉本です。
今回のテーマは「立体の切断による変化」。
立体図形には「立体を何ヶ所か切断し、残った立体について点・辺・面の数や表面積を求める」といった問題があります。
このような問題は「切断後の立体図形そのもの」について考えることで、点・辺・面の数や表面積を出すこともできますが、切断後に複雑な立体になる場合などは、図を描いて数えたり、一つひとつ確認したりするのが難しい場合もあります。
そのようなときは「1回の切断によって、どのような変化が起きているか」に注目するのがおすすめ。1回切るごとに起こる変化に“法則性”を発見できれば、立体図形全体を考えるよりも簡単に解くことができる場合があるからです。
そこで今回は「切断による変化」に注目しながら、立体図形の点・辺・面の数、表面積を求める問題について解説します。
Contents [hide]
- 問題1:立体切断による点・辺・面の数の変化
- 問題2:立体切断による表面積の変化
- まとめ
問題1:立体切断による点・辺・面の数の変化
まずは、点・辺・面の数を求める問題から見ていきましょう。
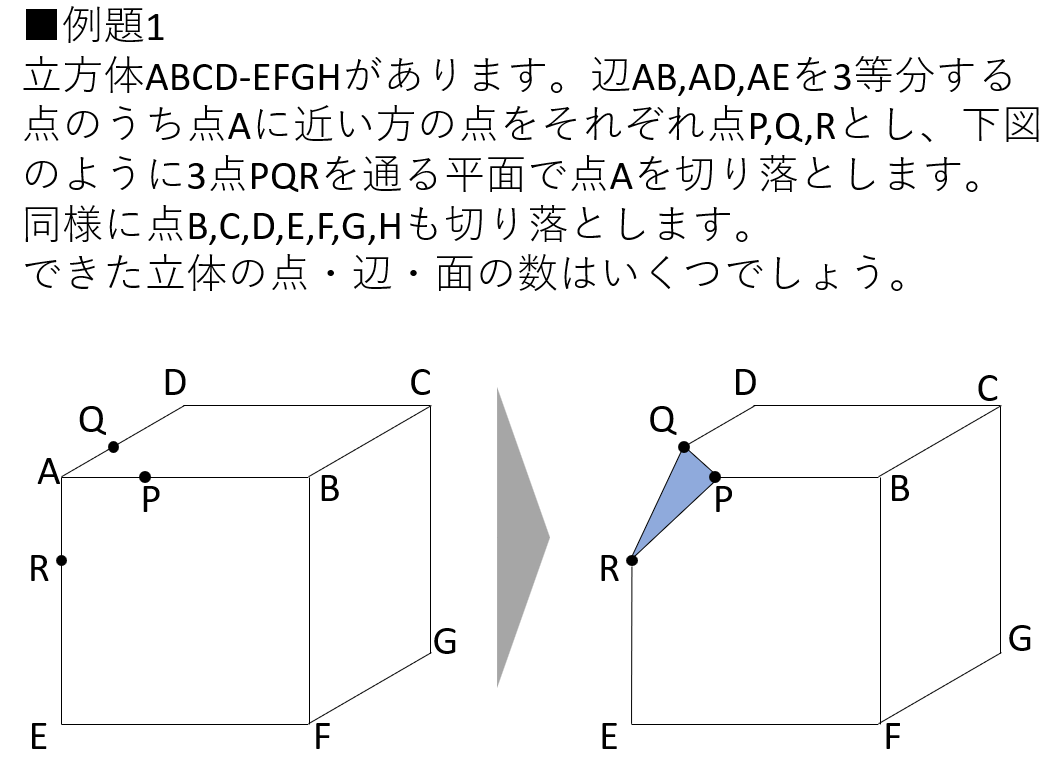
点Hは、点Dから真下におろした位置にあります(今回は目で見て数えることができないように、見取り図ではあえて隠してあります)。
問題で指示されている切断方法によってできる立体の見取り図は、次の図のとおりです。
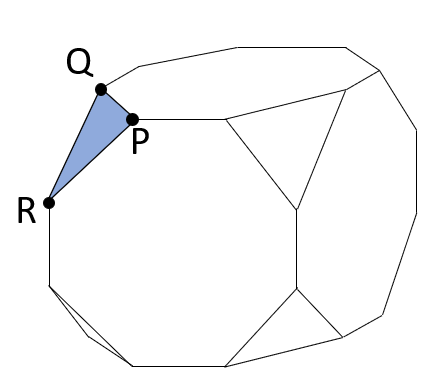
この問題を考えるとき、できた立体の「裏側の見えない部分」を想像して、点・辺・面を数えることも不可能ではありません。ただ、立体を頭のなかでイメージするのが苦手な場合には少し難しいかもしれませんね。
そのようなお子さんは、
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

