
九九ではちょっと足らない|桜井信一コラム「下剋上受験」
さあ、GWが始まりました。
6年生は塾でビシビシとしごかれているでしょうから、今夜は4年生や5年生のお子さんがいるかた向けのお話しをさせてください。
計算が得意というかたもいれば、うちのように「まずは計算から」というかたもいるでしょう。
まずは計算からというかたにぜひ読んでいただきたいと思います。
小学校で九九を習いますよね。だから私のような親の場合それで十分たりていると信じていたんです。
しかし、実際は九九だけではダメだった……。
そんなレベルの低い話でよければご覧ください。
まずはこちらを。
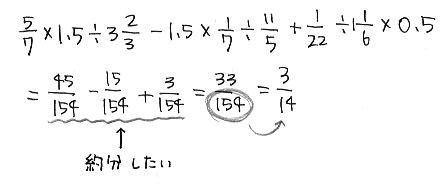
皆さんのようにパソコンをうまく使いこなせない私としては分数は手書きでスキャンとなってしまいます。ちょっと見えにくいかもしれませんがお許しください。
これは、東京都渋谷区にある渋谷教育学園渋谷中学校の平成21年度の最初に出題された計算問題です。
私たちは計算問題をかなり研究しましたが、ただややこしいだけの計算問題っていうのはあまりなく、どうやらちゃんと出題意図があるようなんです。入学試験ですから当たり前のことなんですけどね。
クオリティの低い計算問題集だと単に計算がややこしいだけで出題意図のないやつがかなり含んでいることがあります。
あれはいけませんねぇ~。
我が家のように短期勝負の場合は時間の無駄。ちょっと気付くのが遅れたおかげでずいぶん無駄な時間を費やしました。計算ドリル代は勘弁してやるから、時間だけでも返せ!って気分です。
さて、計算問題が数問出題される中学校の場合、出題意図が同じ問題が続くことはあまりない。
私が経験した範囲だけいうと、まずない。渋渋の場合もこのあとの2問目は意図が異なります。そこは今回は省略して1問目のこの計算問題だけに着目します。
例えば、この渋渋の1問目の場合、最後に分母が154になった時点でちょっとでも約分があたまをよぎっているようではいけませんね。
結果的に約分できないことに気付いたとしても、その約分したくなる気持ちが厄介なんです。
「約分できないということは苦労してここまできた途中計算に間違いがある?」なんて気がしてくるともう集中力を欠く。
結局計算問題って色々よぎるときにミスが起きますよね。最後まで冷静に解き終えるには出題意図に気付かないと安心できない。
このときに素数の倍数を覚えているとちょっと有利だなぁ~なんて私は思います。
11、22、33、44・・・・121、132、143、154
13、26、39、52・・・・182、195、208、221
17、34、51、68・・・・187、204、221、238
19、38、57、76・・・・209、228、247、266
私は、23までの倍数を300まで書き出した表を作っておいて、約分する機会があったときにその数字にマルをつけていったんです。
すると、23の倍数は過去問ではほとんど出題されていないことがわかりました。
11と17がやや人気ですが、まあ全体的にまんべんなく出てますね。
これを九九のように暗記する必要はないと思うんです。
「こいつ見たことある顔だな」と思うだけで十分。
57っていう数字は九九では登場しないじゃないですか。
だから九九を暗唱するときに57って勘違いすることはまずない。
それは普段見慣れないやつだからですね。57君は。
それと同様に素数の倍数と顔見知りになるとかなり有利だと思います。
ところで、この11の倍数はちょっとコツがあります。倍数判定法ってやつですね。
お馴染みの倍数判定法というと、
2の倍数・・・偶数
3の倍数・・・各桁の和が3で割れる
6の倍数・・・上記を同時に満たす
9の倍数・・・各桁の和が9で割れる
他に7も8も判定法がありますが、桁数が大きくならないと使えないので中学受験では出番がなさそうです。
でも11の判定法は3桁の数字を瞬時に見分けることができるので、約分するときにかなり有利だと思います。数列の問題のときも何度か使いました。
11の倍数は1つ飛ばしの数の和を比べたとき、同じか11の差がでます。
中学受験の計算ではほとんどが3桁までの数ですので、121、132、143、などをよ~くみてください。
121の場合・・・1+1と2が同じ
132の場合・・・1+2と3が同じ
143の場合・・・1+3と4が同じ
209の場合・・・2+9と0が11違い
308の場合・・・3+8と0が11違い
だから渋渋の分母154はあきらかに11の倍数です。
まぁ例に使わせてもらっただけで、この問題の場合は分子が33ですからバレバレですけどね。
でも「11で割れそう」ではイマイチですね。
「割れる!」じゃないと。
確信を持って計算するということは大事だと思うんです。
「おっ、出題意図みっけ」みたいな。
これ、ご存知の方は結構いるのでしょうね。私には大発見でも皆さんには当たり前のことって結構ありますから。しかし、大発見だから使えるんです。
計算問題だけではなく、後々出てくる数列や少し難易度の高い整数問題。図形がからんだ倍数約数の問題でも大活躍します。
深く考えずに計算が早い子って小学校に結構いますよね。小さい頃から計算に慣れているんでしょう。
でも、数字の表情を見つめる目を持った方がたかが計算を数列や図形に活かせる。
今からお子さんが本格的に中学受験勉強にとりかかる皆様。もし、お子さんが知らなかったらぜひ教えてあげてください。
そして万が一、親も知らなかったという方がいらっしゃれば、お子さんに教えるときにひとこと付け加えてください。
誰からの情報かという点を!
ここが重要ですから(笑)
2014.5.4 am 1:40
桜井信一
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

