【小4算数／場合の数】樹形図を使わない場合の数｜中学受験のツボ［算数編］

国語｜理科｜社会

髭之教育会代表の有賀です。

何通りあるか、何個あるかを数え上げる「場合の数」に対応する力は、近年の受験算数では必須の学力になっています。

特殊算のように、解法のパターンがつくりにくい単元ですが、「秩序をもって物事をとらえる力」を獲得するには、とても良い単元です。

場合の数を学ぶうえでまず学ぶ内容は「樹形図」です。

数え上げる順序を決めて、取りこぼしなく樹形図を描けるようにしましょう。基本となる樹形図をマスターしたら、次の段階に進みます。

今回は「樹形図を使わない場合の数」について説明します。

カリキュラムによっては、4年生で学ばない内容かもしれませんが、そんなに難しい内容ではありません。

ぜひ、挑戦してみてください。

まずは普通の道の問題で理解する

まず、次の問題を考えてみましょう。

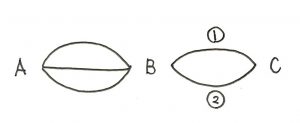
一般的には、かけ算を使って答えを出すことが多い問題です。

ですが、今回は解法の内容を理解することが目的なので、ちょっと遠回りして考えてみます。