【小6算数／文章題】つるかめ算・不定方程式の見極めと解法｜中学受験のツボ［算数編］

国語｜理科｜社会

こんにちは。
株式会社ORA-Trio杉本です。

今回のテーマは「不定方程式と3段つるかめ算」。

受験生が混同しがちな、2種類の問題について解説します。

この2種類の問題は、問題文や条件が非常に似ています。不定方程式にたったひとつ条件が加わるだけで、3段つるかめ算の問題となります。

ただし、解くときに必要な解法は、実はまったく異なります。

つまり、「問題文の条件の確認と、解法の判別」が非常に大切なポイントになるのです。

それぞれの問題の条件を理解したうえで、「今回はどちらの問題か」を正確に判断し、解き始められるようにしておきたいですね。

不定方程式の条件と解法

まずは「不定方程式」について解説します。

以下の例題を見てください。

3つの数（ひとつの袋あたりのおかしの数）があり、それぞれにかける値（袋の個数）の合計と、積の合計（おかしの数）がわかっている、という状態です。

不定方程式と呼ばれ、答えが複数考えられる場合があります。

このような問題は、3段の面積図で解くのがおすすめです。

として面積図を描くと、以下のようになります。

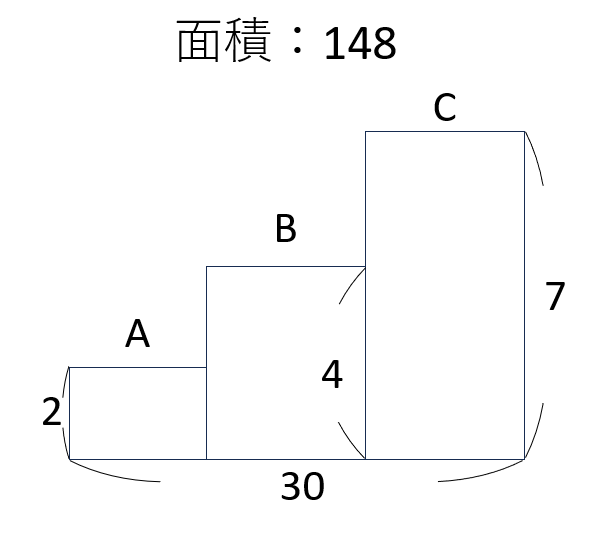
ここで、いちばん下の段の長方形を切り取ると、その部分の面積は 2×30＝60。

すると、残りの部分の面積は、148－60＝88 となります。

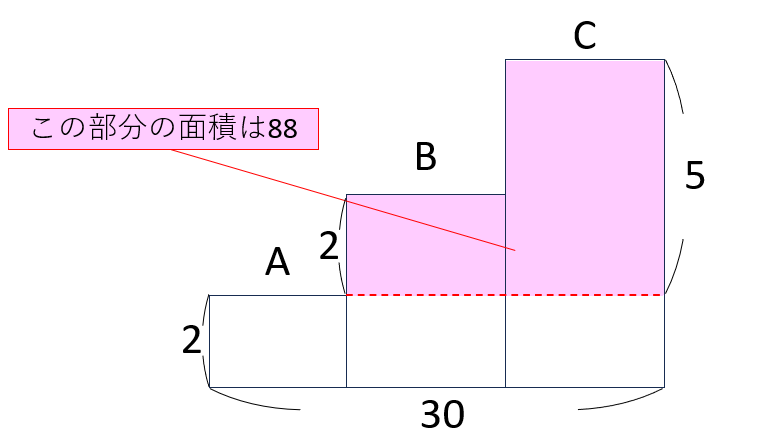
この部分の縦の長さは2と5なので、「袋Bの数を◯、袋Cの数を□」と書くと、以下の式が成り立ちます。

2×◯＋5×□＝88

◯と□の和が30以下であることに注意しながら書き出していきます。

すると、◯と□の数として考えられる組み合わせは、以下の4つとなります。

3つの袋の数の合計は30個なので、それぞれのときの袋Aの数を求めることができます。

まずは、この不定方程式の解き方をしっかり身につけましょう。

3段つるかめ算

次は、「3段つるかめ算」と言われる問題です。

先ほどの問題との違いに注意しながら、問題文を読んでみてください。

例題1との違いに気づいたでしょうか？

「袋Cは袋Aの2倍あります」という条件が追加されましたね。

この問題は「3段つるかめ算」と呼ばれ、答えがひとつに定まる問題です。

3段つるかめ算は、表を使った解法がおすすめです。

解法は以下の通りです（ぜひ一緒に表を描きながら考えてみてください）。

1、袋A、B、Cの個数とおかしの個数を表にして考える

30袋すべてが袋Bだと考えると、以下の表のようになる。

2、袋Bを減らし、袋Aと袋Cを増やしておかしの個数を確認していく

「袋Cは袋Aの2倍ある」という条件があるため、1回の操作で「袋Aを1個、袋Cを2個増やし、袋Bを3個減らす」という操作となる。

このとき、おかしの個数は、

2×1＋4×27＋7×2＝124個

となり、4個増える。

3、おかしの個数は合計148個なので、（148－120）÷4＝7回、同じ操作をすれば良いことがわかる

4、ここまでくれば、袋Bの数を次のように求められる

袋Aは7個
袋Cは7×2＝14個
袋Bは30－（7＋14）＝9個

このように3段つるかめ算は、計算によって答えをひとつに絞ることができます。

条件がひとつ加わるだけで、まったく異なる単元の問題、異なる解法となることが理解できたでしょうか？

• どのような条件があれば、不定方程式か
• どのような条件があれば3段つるかめ算か

をしっかりと整理しておきましょう。

まとめ

今回は、不定方程式とつるかめ算の見極め方・解法の違いについて解説しました。

今回紹介したふたつの問題のように、似ている問題こそ「問題の条件と使うべき解法」をどこまで整理できているかが問われます。

あせらず、丁寧に習得していけると良いですね。

それではまた！

※記事の内容は執筆時点のものです