【小6算数／平面図形】図形を描く順番の考え方と手順｜中学受験のツボ［算数編］

学習連載中学受験のツボ［算数編］

専門家・プロ

2022年9月21日杉本啓太

保護者向けに中学受験の4教科のツボを解説。 算数編 は杉本啓太先生と有賀隆夫先生が担当します。

- 算数以外の3教科はこちら -

こんにちは、杉本です。

今回のテーマは、「図形を描く順番の考え方」です。

先月の記事「問題を解くヒントは「図形を描く順番」にあり」で「複雑な問題を解くときには、図形を描く順番を意識するのが有効な場合がある」とお話ししました。

今回はその具体的な方法について、例題を解きながら「最初に引く直線はどれかな？」と、具体的な手順を解説していきます。

ぜひご家庭でも、お子さんと一緒に実際に図を描きながら「ああ、この図はこういう順番で描かれたんだ！」と実感してもらえればと思います。

Contents

「最初に与えられる図」から一つひとつ直線や点を追加しよう

まずは、長さを求めるところは考えず、図を描く順番を考えるトレーニングだけやってみましょう。

そのときに気を付けてほしいのは、以下の3点です。

①　「最初に与えられる図は何か」を確認する
②　直線や点は一つひとつ追加する
③　直線を引くときは「すでにある2点を結ぶ」ことを意識する

以下の問題を見てください。

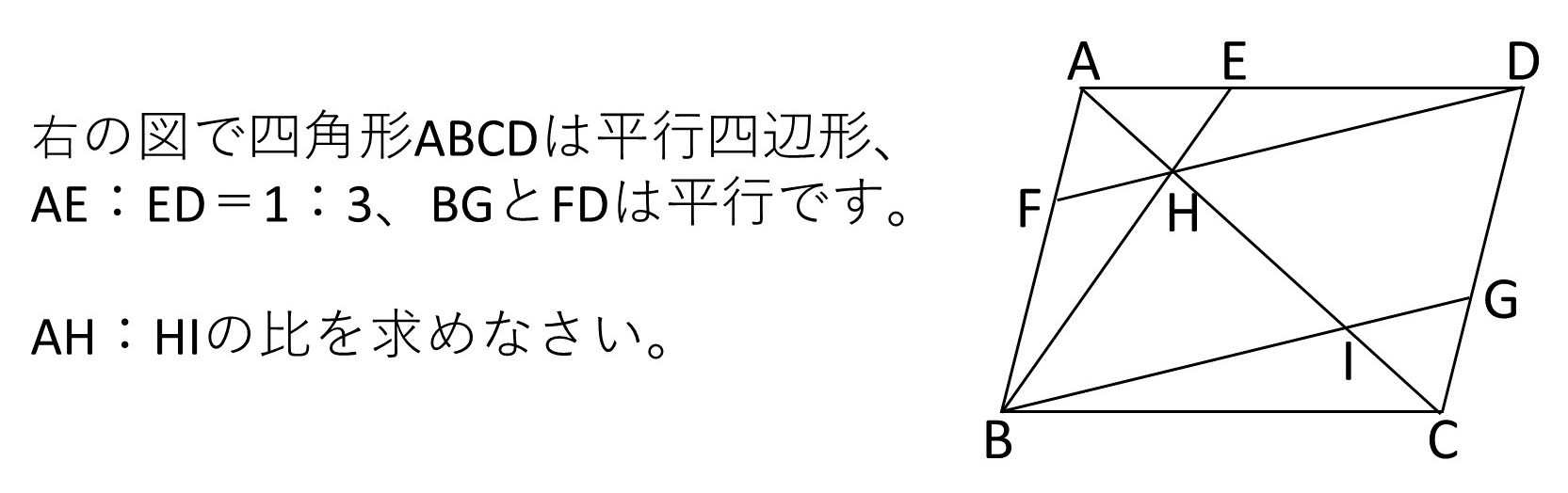
※今回はトレーニングなので、文中の「AH：HIの比を求めなさい。」の部分は一旦置いておいてください。

この問題の場合は、

最初に与えられる図：平行四辺形ABCD、点E
追加で引かれた線：AC、BE、DF、BG

となります。

では、平行四辺形ABCDが描かれた状態から問題の図が完成するまでには、どのような手順で描いていけばよいでしょうか？

続きは会員の方のみご覧いただけます