四則混合の計算問題に強くなろう｜家庭で教える算数

特別な話ではないけれど、意外とできない子が多いのが四則混合の計算問題です。大学生でもミスをしてしまうことがありますから、親御さんがお子さんの勉強をサポートされている場合、苦労されることもあると思います。今回は、お子さんを四則混合の計算問題に強くするための計算の工夫をご紹介します。

四則混合の計算問題に役立つ「かたまり」のイメージ

四則混合の計算問題に対応するには、「×÷＋－」いわゆる「かけ・わり・たし・ひき」の順番で計算する、というイメージをお子さんが持っているとよいです。ですが、この「順番」で計算するときに、間違えやすいポイントがあるので注意が必要です。

例えば

12－24＋44＝

という計算の場合、

• 12から24は引けない
• ＋から計算するから、24＋44＝68にしたら12から引けない

のような間違いを起こすケースです。

こういった、間違いを防ぐために、次ような「かたまり」をつくるイメージを持たせましょう。

次にこの〇で囲んだ「かたまり」の順番を入れ替えて計算するようにします。

「＋」「－」の順で並べ替えていくと、次のようになります。

このように、「かたまり」にしてから、順番を入れ替えて計算をすれば、無理なく計算することができるようになります。

「かたまり」で順番を入れ替える

ここで必要な知識は「＋」と「－」は「順番を入れ替えることができるよ」というだけでなく、「かたまりごと入れ替えることができる」ということです。同じように「×」と「÷」も順番を入れ替えることができます。

ただし、「×」と「＋」の組み合わせや「÷」と「＋」の組み合わせでは入れ替えることができません。

四則混合計算のルールを整理すると、次の図のようになります。

四則混合計算のルール

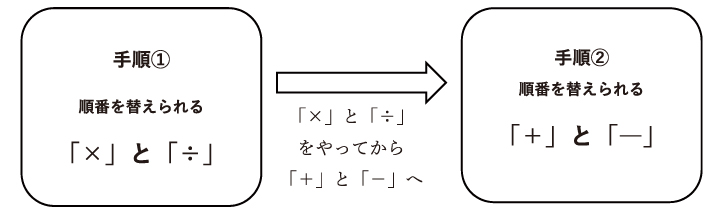
「×」と「÷」が混ざっている場合の考え方

前述のように、「×」と「÷」は順番を入れ替えることができますが、これも「＋」と「－」と同じように「かたまり」で動かしていく必要があります。そして、「×」と「÷」の場合は次の2つの計算の工夫をするよう意識します。

「×」と「÷」の計算の工夫［1］：割り切れる組み合わせで並べ替える

例えば、

36×9÷4×2÷3＝

という式があった場合、まず次のような「かたまり」をつくります。

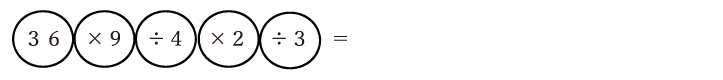
次はどのように組み合わせたら簡単に計算ができるのか、を考えていくのですが、割り切れる組み合わせになるように並べ替えていきましょう。

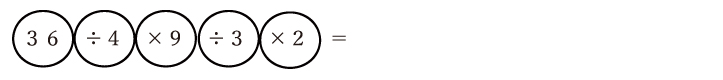
こうすると、「36÷4」と「9÷3」が割り切れるので、

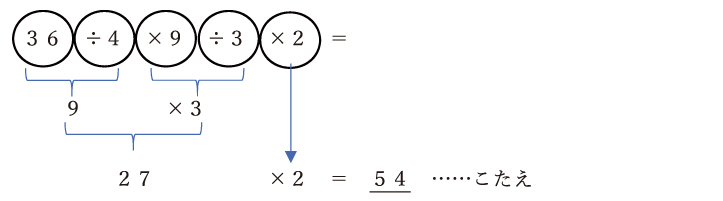
となります。

「かたまり」で上手に並べ替えることで大きな数の筆算を減らすことができ、計算ミスが減るので、ぜひマスターさせておきたい習慣です。頭の中でパッと組み合わせをつくって計算ができるようになると良いですね。

「×」と「÷」の計算の工夫［2］：分数を使う

もう一つの工夫は分数を使うことです。分数を学習しているのであれば、「×」と「÷」の組み合わせは分数で整理をするのをおすすめします。

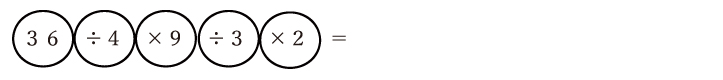
この計算であれば「×」の「かたまり」を分子、「÷」の「かたまり」を分母に分けて整理しましょう。次の図のようにします。

「÷」の「かたまり」を分母に移した時に「×」へ変えるようにします。そうすると、分母と分子で約分ができるようになりますよね。

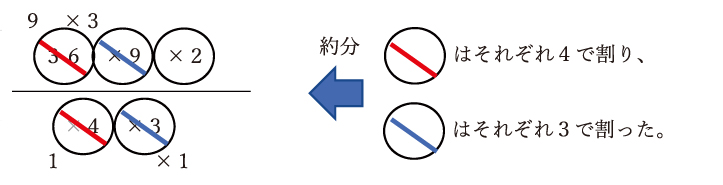
これで、分母は1×1になるので1です。分母が1になったら分母は省略できますので、この計算は

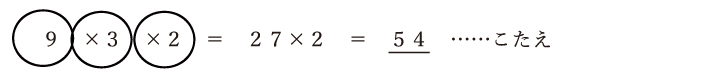
一見すると面倒に見えますが、約分に慣れれば大きな数をできるだけ簡単にしてから計算をできるようになるので、計算ミスを減らすことに役立ちます。

四則混合の計算で工夫するのは何のため？

そもそも計算の工夫をめんどくさがって、大きな数の計算を力技でやった結果、四則混合の計算でミスをするというケースはとても多いです。計算ミスを減らすには「いかに計算を簡単にできるように整理するか」が非常に重要なのですが、工夫をする理由はそれだけではありません。

中学入試においては限られた時間のなかで問題を解くことが要求されます。そして、大学入試改革の影響で中学入試でも思考力がより重視されてくることでしょう。そうなってくると、試験時間の中で「考える時間をどれだけ確保することができるか」は重要なポイントになっていきます。

ですから、工夫をして計算をより「早く」「正確」に処理できる力を身につけておくと「計算のための時間」が減り、「考えるための時間」を増やすことにつながるのです。計算の処理能力を高めることが結果的に落ち着いて考える時間を生み、思考力向上に役立っていくのです。

■「家庭で教える算数」バックナンバー

• 今さら聞けない割合の計算の基本知識｜家庭で教える算数
• ［算数］計算の工夫でかけ算を素早く処理する｜家庭で教える算数
• 小学校にあがる前に身につけたい「試行錯誤する力」｜家庭で教える算数
• 小学校にあがる前に身につけたい「比べる力」｜家庭で教える算数
• 四則混合の計算問題に強くなろう｜家庭で教える算数

※記事の内容は執筆時点のものです