［算数］計算の工夫でかけ算を素早く処理する｜家庭で教える算数

2ケタの数字程度のかけ算は工夫して簡単に処理できるのなら、わざわざ筆算をせずに、計算の工夫で処理する方がよいです。

というのも、「計算の処理に時間を費やす」ということは、それだけ思考する時間を失うということであり、「計算を早く正確に処理できる」ということは、問題に対して思考する時間を増やすことにつながるからです。

計算を工夫して「より早く、正確に処理する技術」を身につけることは重要です。こういった計算の工夫にはいくつかのテクニックがあります。今回はそのなかから基本的な計算の工夫を3つ取り上げて紹介します。

計算の工夫1 ―― 1つ減らす、1つ増やす

例えば、「16×21」という計算をする場合、もしこれが「16×20」なら暗算でも「320」と計算ができるのではないでしょうか。

では、「16×21」と「16×20」の違いは何でしょう。

このように考えると、「16×21」というのは「16×20」に「16」を加えただけ、ということがわかると思います。

ですから「16×21」は「320＋16」で「336」という計算ができるのです。

同じように、「17×19」という計算をする場合を考えてみましょう。この場合も「17×20」から「17」を引けばよいということがわかりますから、「340－17＝323」という答えが暗算でできるようになるのです。

「1つ減らす、1つ増やす」という計算の工夫はとても単純なものだとわかると思います。雑誌や本で紹介される「〇〇式」といった計算手法もよいのですが、シンプルに考えてできる範囲の工夫であれば、基本的に「やり方を忘れた！」という状況になりにくいですよね。ですので、この「1つ減らす、1つ増やす」考え方はおすすめの計算の工夫です。

計算の工夫2 ―― 「100」をつくる

「16×25」のような計算のときに使う計算の工夫です。「25×4」は「100」になるという性質を利用します。

「16×25」をもう一度考えてみると……、

という形に分解できるのがわかりますよね。

「4×25」は「100」ですから、「4×4×25」＝「4×100」に変えることができます。そうすれば、簡単に答えが「400」と求められるようになります。

「4の倍数×25」のときに活用できるとよい計算の工夫ですね。

計算の工夫3 ―― 小数から分数へ変換する

「0.25」は\(\frac{1}{4}\)、「0.75」は\(\frac{3}{4}\)になりますよね。このように小数を分数に変換できるものが、いくつかあります。これらを上手に活用して計算の工夫をおこないます。

この計算の工夫は、特に小数と分数が混ざった計算のときに利用する工夫です。特別なものではなく、一般的にも習う計算の工夫ですが、念のために紹介いたします。

このような計算の際に、「0.25×48」の筆算をやっていては単純な計算ミス、小数点をつけ間違えるといったミスを誘発するポイントが増えてしまいます。

ですので、「0.25＝\(\frac{1}{4}\)」と置き換えて計算をします。

こうすると、分母の「4」と「48」を約分するだけで簡単に答えが「12」とわかるはずです。

以下に小数と分数の変換で覚えておきたいものを並べますので、まずはここから覚えてしまいましょう。

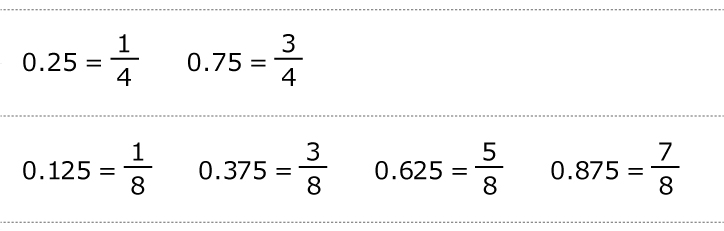
上記の中に「0.5」は入っていません。「0.5」は「\(\frac{1}{2}\)」で、単に半分にすればよく、わざわざ覚える必要なし、ということで省いています。

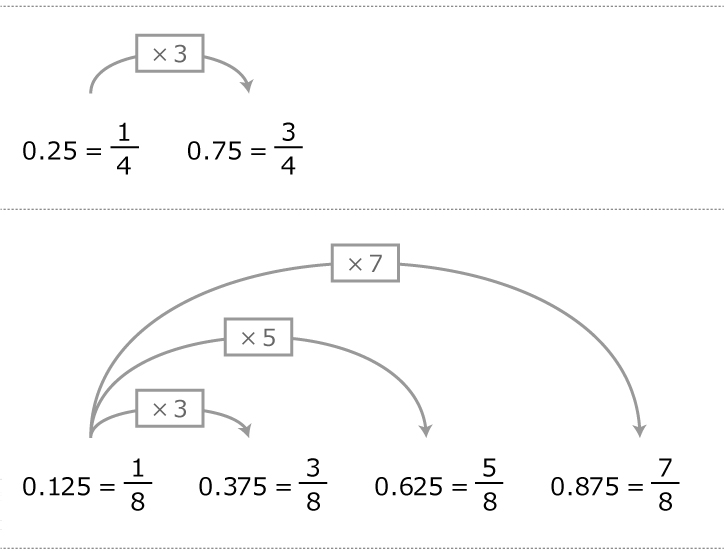
「0.25」と「0.125」を覚えておけば、下の図のようにあとはその倍数で判断することもできます。慣れるまでは、それぞれを覚えて、計算に慣れてきたら、暗記する量を減らしていくのもよいでしょう。

計算の工夫で正確に早く処理する力を身につけましょう

かけ算を例に計算の工夫の例を3つ紹介しました。正確に早く処理する力は、中学受験の勉強に限らず、その後の学習でも役に立ちます。お子さんが計算問題でつまずいている場合は、複雑な筆算をしていないか、紹介した計算の工夫ができているか、ぜひ確認してみてください。

■「家庭で教える算数」バックナンバー

• 今さら聞けない割合の計算の基本知識｜家庭で教える算数
• ［算数］計算の工夫でかけ算を素早く処理する｜家庭で教える算数
• 小学校にあがる前に身につけたい「試行錯誤する力」｜家庭で教える算数
• 小学校にあがる前に身につけたい「比べる力」｜家庭で教える算数
• 四則混合の計算問題に強くなろう｜家庭で教える算数

※記事の内容は執筆時点のものです