
【小6算数/差集め算】「どうそろえるか」の視点を持とう|中学受験のツボ[算数編]
こんにちは。
株式会社ORA-Trio杉本です。
今回のテーマは「差集め算」です。
商品の金額や、ひとつのイスに座った人数の違いに注目して解いていく。
このような形で出されることが多い問題ですね。
差集め算にはいくつかの種類があり、その種類に合った解法を習う子も多いと思います。ただし、一見すると違う解法でも、実は根本的な考え方は同じである場合もあります。
今回は、差集め算の基本・応用問題について解法を解説します。
それぞれの解法自体を覚えるのではなく、「異なる解法に共通している視点」に注目しながら読んでみてください。
基本的な差集め算の解法
まずは、基本的な差集め算の解法を解説します。
以下の例題を見てください。
例題1
クラスの子供にチョコレートを配ります。1人2個ずつ配ると63個あまります。1人4個ずつ配ると1個あまります。チョコレートは何個あるでしょう。
問題の内容を図にしてみましょう。以下のようになります。
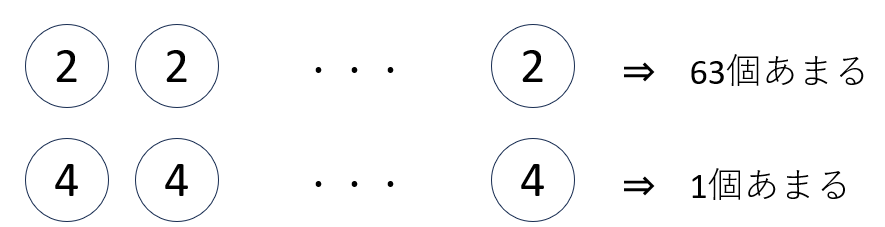
ふたつの配り方を比較すると、
- ひとり当たりに配った個数の差は2個
- 残った個数の差は62個
となります。
ひとり当たりの差の2個が積み重なった結果、全体では62個の差になったということですね。
このことから、クラスの子供の人数は、
62÷2=31人
と求めることができます。
よって、チョコレートの数は、
31×4+1=125個
となります。
まずは、この基本的な考え方を身につけておきましょう。
人数を「そろえる」差集め算
次に、応用問題にチャレンジしてみましょう。
以下の例題を見てください。
例題2
クリスマス会で子供にあめを配ります。参加予定の子供に1人5個ずつ配ると5個あまる予定でした。しかし4人が欠席したため、1人6個ずつ配ったところ、4個あまりました。あめの数は何個でしょう。
今回も、問題の内容を図にすると、以下のようになります。
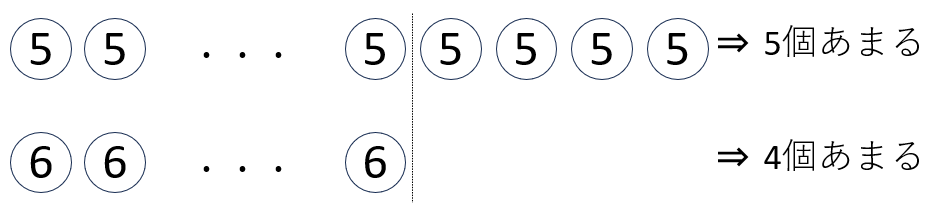
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

