【小6算数／平面図形】相似と連比を使った定番問題を攻略しよう｜中学受験のツボ［算数編］

国語｜理科｜社会

こんにちは。
株式会社ORA-Trio杉本です。

今回のテーマは「平面図形」です。

相似を使った問題のなかで、少し応用的な内容に入ったときに出てくる「複数の相似から連比を使って辺の比を求める問題」について解説します。

多くの学校で出題されることも多い、定番の問題です。相似を学習した直後に取り組むと少し難易度は高く感じるかと思いますが、確実に正解できるようにしておきたいですね。

次のようなポイントに注意し、いっしょに図を描きながら練習してみましょう。

まずは答えまでの道筋をイメージしよう

今回は、以下の例題を題材にポイントを解説していきます。

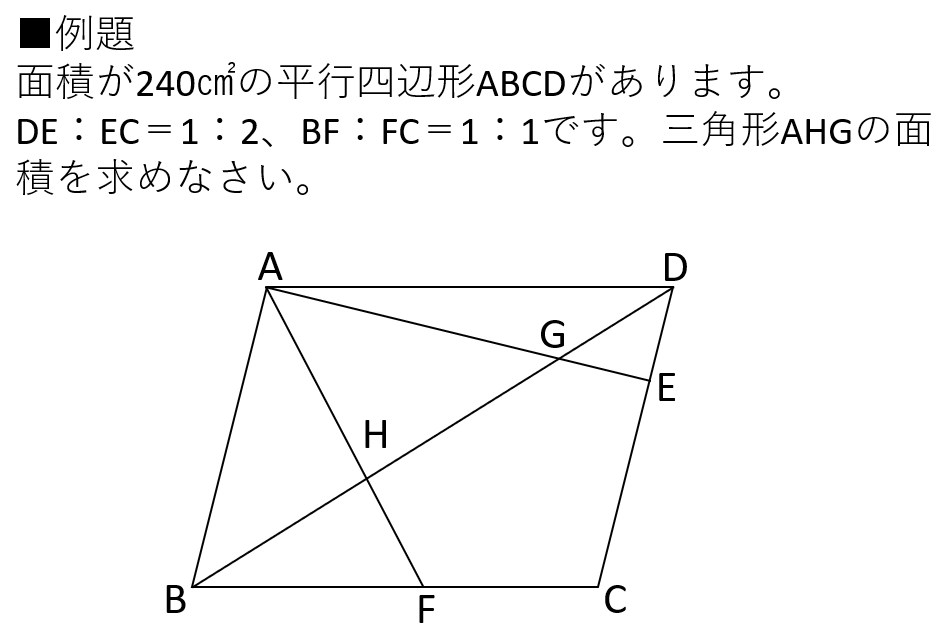
最初に考えてほしいのは「どのような流れで三角形AHGの面積を求めるか」ということです。

辺の長さについての情報が与えられていませんよね。そのため、「底辺×高さ÷2」などで求められないことは、すぐに気づけるでしょう。

そこで、「面積の比」を使う方法を検討します。

そして、ここでのポイントは次の2点です。

ここまでくれば、「BH：HG：GDの比を求めよう」という方針で考えを進めることができますね。

平面図形は「慣れ」の要素が強い単元でもあります。上記のようなポイントは、類題演習を重ねることにより、頭に浮かびやすくなってきます。

ですから、粘り強くトレーニングできると良いでしょう。

相似を見つけるときのコツ

次に、相似を見つけるときのコツについてお話しします。

まずは、BH：HDについて考えてみましょう。

この比を考えるときは、真ん中の点である点Hに注目します。BH：HDという比は「AFとBDが交わった点Hによってできた」と考えるのです。

そうすると、「三角形FHBと三角形AHDの相似」に気づきやすくなるでしょう。

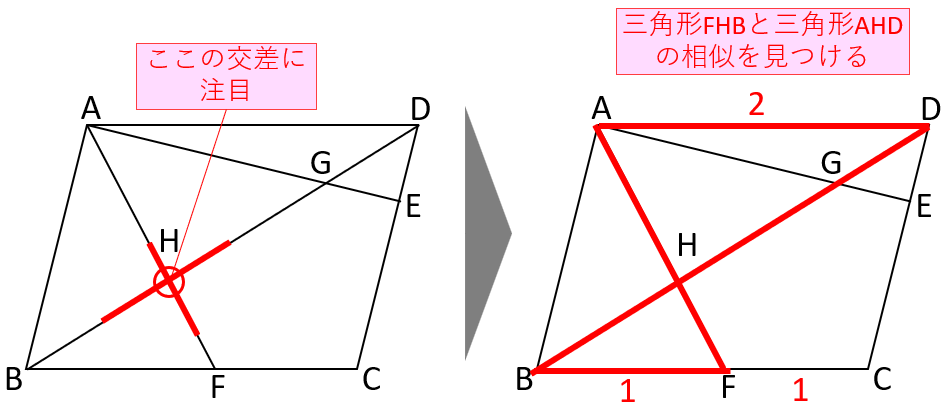
三角形FHBと三角形AHDの相似比は、FB：ADより1：2なので、BH：HDも1：2とわかります。

同様に、BG：GDも、三角形ABGと三角形EDGの比に注目すれば良いですね。